initiation à la démonstration , prérequis theorèmes

	Classe de 4^ème collège .	Programme classe de 4^ème collège..


Pré requis:		Vers le corrigé
« lire un énoncé et Rédiger »
Collège : les définitions ;propriétés et description des quadrilatères
Collège : les définitions ; propriétés et description des triangles.
Liste des Objectifs

ENVIRONNEMENT du dossier:

Index warmaths

NOTIONS

Objectif suivant :

1°) La démonstration « série 1 » .

2°) Suite

Liste des cours de géométrie plane

tableau

DOSSIER : « Bases sur LA DEMONSTRATION » au collège


	Fiche 1 : Constations et démonstration.
	Fiche 2 : A quoi sert un théorème ?
	Fiche 3 . Quelles propriétés utiliser dans les démonstrations ?
	Fiche 4 : A propos des dessins .
	Fiche 5 Droites parallèles.
	Fiche 6 : Parallèles coupées par une sécante. (angle alterne , externe ……)
	Fiche 7 : Une façon de démontrer que des droites sont parallèles.
	Fiche 8 : Somme des angles d’un triangle.
	- Somme des angles d’un quadrilatère non croisé.

	COURS

	Fiche 1 : Constations et démonstration.	Info ++ droites remarquables et triangle rectangle
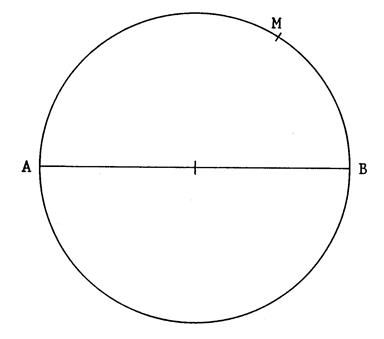
	Ci-contre voici un cercle . [ AB] est un diamètre de ce cercle. « M » est un point de ce cercle. ( « M » est distinct de « A » et « B » ). Activités : Tracez les demi-droites [ MA et [ MB. A l’aide de votre rapporteur mesurez l’angle : . (angle de sommet « M ») Vous trouvez approximativement : ………………..°
	- Prenez sur le cercle un nouveau point distinct de « A » et « B ». Appelons le « N » . - Tracez les demi-droites [ NA et [NB , mesurez . Vous trouvez approximativement : ………………..°
	- Choisissez sur le cercle d’autres points (distinct de « A » et « B ».) - Tracez les demi- droites , mesurez l’angle . - Vous trouvez approximativement : ………………..°
	A ) Les essais successifs que vous venez de faire vous suggèrent l’énoncé suivant :
	Etant donné un cercle de diamètre [ AB] , pour tout point « M » du cercle distinct de « A » et « B » , l’angle . est de …90°….

	Ces activités appellent deux remarques : 1°) Comme il y a une infinité de possibilités de prendre « M » sur le cercle , Vous ne pouvez pas mesurer tous les cas . Vous ne pouvez donc pas dire que « dans tous les cas » = 90° ; 2°) Les mesures que vous venez d’effectuer , aussi précises soient – elles , sont toujours « approximatives » : 90,5° ; 89,7° ; 89,99° ; ……. Vous ne pouvez donc pas dire que est exactement égal à 90° ;
	B ) Vous concevez alors que pour pouvoir affirmer ce que vous venez de constater, il est indispensable de faire un raisonnement. Pour cela, partant de ce qui est donné et que l’on appelle « l’hypothèse », grâce à un raisonnement déductif que l’on appelle une « démonstration » , on aboutit à ce que vous avez constaté et que l’on appelle « la conclusion ». Dans l’exemple que nous avons vu , l’hypothèse est :
	[ AB] est le diamètre du cercle, « M » est un point quelconque du cercle « M A » , « M B ».
	La conclusion est ……… = 90° ……
	La démonstration sera faite ultérieurement…….( leçon 14 ) , vos connaissances que vous êtes supposées posséder en mathématiques ne sont pas suffisantes pour la faire maintenant ……..

	Ø L’énoncé d’une propriété importante que l’on a démontrée s’appelle « un théorème ». Il se présente de la manière suivante ( prés traduction) : « si l’hypothèse est vraie , alors la conclusion est vraie. » Sous-entendu , grâce à une démonstration qui a été faite une fois pour toutes. Ø Dans le cas présent , le théorème pourrait s’énoncer de la manière suivante :
	Théorème : Si [ AB] est un diamètre d’un cercle et « M » un point quelconque de ce cercle , « M A » , « M B »., alors est égal à 90° .

	Fiche 2 : A quoi sert un théorème ?

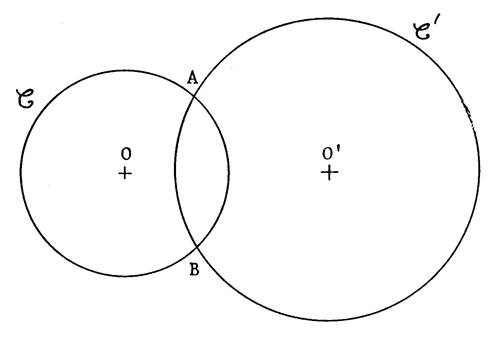
	Voici , ci – contre , deux cercles « C » et « C’ »de centre « O » et « O’ » et qui se coupent en « A » et « B ». Tracez ( AO) et ( A O’) . ( AO) recoupe le cercle « C » en « D ». ( A O’) recoupe le cercle « C’ » en « E » . A votre avis , les points « D » , « B » , « E » sont-ils alignés ?...... Apparemment « oui » ….. ! Mais peut-être sont-ils « presque alignés » et peut-être qu’en faisant une autre figure, on ne les trouverait pas du tout alignés.

	La seule façon d’en être certain, c’est de faire une………………………………………. Pour cela on va vous aider car vous n’avez pas encore assez d’expérience .
	Pour le cercle « C » que pouvez –vous dire de [ DA ] ? ……………………………………………………. ; Tracez [ AB et [ BD . A quoi cette situation vous fait-elle penser ? …………………………………………………….. …………………………………………………………………………………………………………………………………………. En admettant que cette propriété ait été démontrée ( ce qui se fera dans la leçon n°…), quelle conclusion pouvez-vous tirer dans le cas présent ? ………………………………………………………………….. De même , avec le cercle « C’ », que pouvez-vous affirmer que = ……………………?
	§ Considérons : ; = Donc : = ……° Donc est un angle ……………….. ; donc les points « D » , « B » , « E » sont ………………………………………………

	§ Dans ce qui vient d’être fait , vous avez pu constater que tout n’a pas été démontré. En effet : pour prouver que = 90° , on a utilisé le théorème de la fiche 1 . mais lui , est censé être démontré une fois pour toutes. Vous voyez alors qu’une démonstration apparaît comme une construction dans laquelle on utilise des éléments préfabriqués : Ces éléments préfabriqués sont les théorèmes ( ou propriétés démontrés ou admises ). La rédaction d’une démonstration consistera à faire comprendre au lecteur que l’on est dans la situation d’application de ce théorème ( ou de cette propriété).

	§ Voici comment il faut rédiger cette démonstration : Tout d’abord , commencez par faire l’inventaire des données de problème ( c’est l’hypothèse ) et précisez ce que vous voulez prouver ( c’est la conclusion ) .
	Hypothèse : Les cercles « C » et « C’ » se coupent en « A » et « B ». [ DA ] est un diamètre de « C » [ EA ] est un diamètre de « C’ ».
	Conclusion : ………………………………………………………………………………..
	Démonstration : Dans le cercle « C » , par hypothèse , [ DA ] est …………………………………………………………………….et « B » est un point du cercle donc , grâce au théorème de la fiche « 1 » , = ………………………….. . Dans le cercle « C’ », par hypothèse ,……………………………………………………………………………………….et ……………… ……………………………………………………….. Donc grâce au théorème de la fiche 1 , …………………………….. Puisque = ; donc : = ……° ; donc est un angle , donc les points « D » , « B » , « E » sont ………………………………………………
	Attention : Avant de dire « grâce au théorème …. » il faut bien expliquer que l’on est dans la situation de l’hypothèse de ce théorème .


	Fiche 3 . Quelles propriétés utiliser dans les démonstrations ?
	En rédigeant une démonstration, vous êtes censé vous adresser à quelqu’un. Pour faire des démonstrations, vous avez besoin d’utiliser des définitions et des propriétés . IL est alors nécessaire que celles –ci soient connues de votre interlocuteur. C’est la raison pour laquelle nous allons récapituler dans les premières leçons celles que vous avez rencontrées dans les années précédentes et qui constitueront le catalogue de ce que vous aurez droit d’utiliser dans vos démonstrations. § Nous ne démontrerons pas ces propriétés. Pour certaines , vous en avez déjà fait la démonstration en classe de 6^ème te de 5^ème . Pour d’autres , la démonstration n’a pas été faite car elle est un peu compliquée mais on peut vous affirmer que cette démonstration existe. Pour d’autres , il n’y a pas de démonstration à faire , ces propriétés sont prises comme base , comme point de départ. Les mathématiciens les appellent des « axiomes ». On ne fera pas ici de distinction entre les propriétés admises ou démontrées en 6^ème te de 5^ème et les axiomes . Par contre , les propriétés que l’on démontrera , seront appelées « théorèmes » Voici une propriété qu’il n’y a pas lieu de démontrer :
	Propriété 1 : Par deux points distincts , il passe une droite et une seule.

	Vous pouvez vous demander : « pourquoi énoncer une propriété qui paraît évidente ». Pour la simple raison que si l’on ne l’énonçait pas , rien ne pourrait nous empêcher de dire que : « par deux points distincts il passe plusieurs droites. » Dans cette situation , vous pouvez imaginer , les conséquences qui en découleraient ;: Par exemple : avec 3 points , on aurait plusieurs triangles ayant ces points pour sommets sans que ces triangles soient superposables . Vous voyez alors que cette mise au point est indispensable.


	Fiche 4 : A propos des dessins .

	Toutes les fois que vous aurez à résoudre un problème de géométrie , vous ferez un dessin ( on appelle aussi : figure ). Mais attention, cette figure n’est pas l’objet mathématique de l’énoncé. Cette figure est « une représentation » de cet objet mathématique.
	Exemple : Dans le cas d’une droite, vous tracez un trait comme ci-contre : Mais ce trait n’st pas une droite . D’abord parce qu’une droite est illimitée et ensuite
	Si on regardait ce dessin au microscope , vous verriez quelque chose comme le dessin ci-contre.
	Donc ce « trait » n’est pas une droite mais par convention il représente une droite.

	Un dessin est utile pour avoir une vue d’ensemble des données du problème. Il permet d’avoir instantanément le nom des différents éléments : points , droites , polygones , etc…. Parfois il peut mettre sur la voie lors de la recherche. Mais attention ! En aucun cas un dessin ne peut constituer une démonstration . Si vous dîtes « on voit bien que ….. » . Tu fais une ……………, mais ce n’est pas une ;…démonstration…

	§ Attention aux figures particulières : elles introduisent des propriétés qui ne sont pas dans l’énoncé. Exemples : - Si on vous dit de tracer un triangle quelconque , évitez de le faire « isocèle ». - Si on vous dit de tracer un quadrilatère , évitez de faire un rectangle.


Fiche 5 Droites parallèles.	Info +++@ les parallèles .

Nous allons récapituler ici les propriétés du parallélisme étudiées en « P. 6^ème » et «P. 5^ème » .

Définition : Deux droites parallèles sont deux droites d’un plan qui n’ont pas de point commun ou qui sont confondues.
Si des droites d’un plan ne sont pas parallèles , elles sont « sécantes »…. Lorsque des droites sont parallèles , on dit qu’elles ont « même direction » .

Propriété 2 : Etant donné une droite et un point , il existe une et une seule droite passant par un point et parallèle à la droite donnée.

Autre forme : Si des droites ont un point commun et sont parallèles à une autre droite alors elles sont ……parallèles ……
Cette propriété est communément appelée « axiome d’ Euclide ».
Exemple de démonstration utilisant l’axiome d’ Euclide.
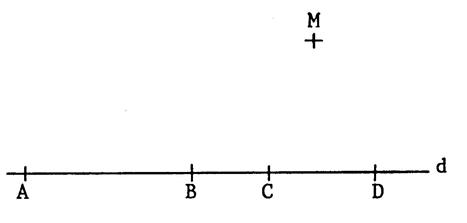
ci-contre , voici une droite « d » et un point « M » quelconque. « A » , « B » , « C » , « D » sont 4 points de la droite « d ». Placez les points « E » et « F » tels que « ABME » et « MCDF » soient des parallélogrammes. Démontrez que « E », « M » « F » sont alignés.
Résolution : On commence par écrire les données ( hypothèse) et la conclusion. Pour cela on extrait de l’énoncé les données essentielles. Par exemple, n’écrivez pas « E est le point tel que « ABME » soit un parallélogramme ». Mais écrivez tout simplement « ABME est un parallélogramme ».
Déroulement de la recherche : ( à ne pas écrire dans la rédaction d’un devoir) Dire que « E », « M » « F » sont alignés. C’est dire que « E », « M » « F » sont situés sur la même …droite…. Ou encore que la droite ( EM )est la …même….. que la droite ( MF ). Un parallélogramme est un quadrilatère dont les côtés opposés sont …parallèles ….. Vous en déduisez donc que ( EM) est parallèle à ( AB) c'est-à-dire à la droite « d » et que ( MF ) est parallèle à (CD) c'est-à-dire parallèle à la droite « d ». On est donc en présence de deux droites passant par un même point ( le point « M ») et qui sont toutes les deux parallèles à un même droite ( la droite « d » ). On est donc dans la situation de l’axiome d’ Euclide : ( EM ) et ( MF ) sont donc parallèles et par suite « E », « M » « F » sont alignés.

Rédaction de la démonstration :
Par hypothèse « ABME » est un parallélogramme donc ( EM) est ….parallèle… à ( AB) et comme par hypothèse « A » et « B » sont situé sur « d » , alors (EM) est parallèle à « d » . Par hypothèse « MCDF » est un parallélogramme donc ( MF) est parallèle à ( CD) et comme par hypothèse « C » et « D » sont situé sur « d » , alors (MF) est parallèle à « d » . Puisque ( EM) et ( MF ) sont toutes deux parallèles à « d » et passant par le point « M » alors grâce à l’axiome d’ Euclide , elles sont parallèles donc « E », « M » « F » sont alignés.

Autre propriété du parallélisme.

Propriété 3 : Si deux droites sont parallèles à une même droite alors elles sont parallèles entre elles.

On traduit cette propriété en disant que le parallélisme des droites est une relation « transitive » et on parle de la « transitivité du parallélisme ».

Exemple : Sachant que « d » est parallèle à « d’ » et « d’ » parallèle à « d’’ ». On dira que « d » est parallèle à « d’’ » grâce à la transitivité du parallélisme.

Fiche 6 : Parallèles coupées par une sécante.	Info +++@ ….sécantes et les angles…

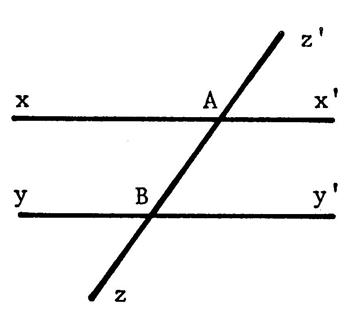
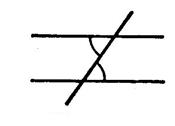
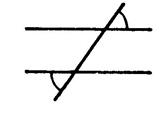
« xx’ » et « yy ‘» sont deux parallèles. Une droite « zz’ » coupe « xx’ » en « A » et « yy’ » en « B ». Ces droites déterminent entre elles « 8 » angles. Passez de la même couleur ceux qui sont égaux. ( Ne coloriez que la région du sommet )
Vocabulaire :
Des angles tels que ..		sont appelés des angles alternes internes
Des angles tels que ..		sont appelés des angles alternes externes
Des angles tels que ..		sont appelés des angles correspondants

Propriété 4 : Si des droites sont parallèles alors toute sécante détermine avec elles/ - Des angles alternes internes égaux. - Des angles alternes externes égaux. - Des angles correspondants égaux.


	Fiche 7 : Une façon de démontrer que des droites sont parallèles.

	Vous avez vu en 5^ème que :
	Propriété 5 : Si deux droites déterminent une sécante détermine avec elles/ - Soit des angles alternes internes égaux. - Soit des angles alternes externes égaux. - Soit des angles correspondants égaux. Alors les deux droites sont ..parallèles……

	Activité :
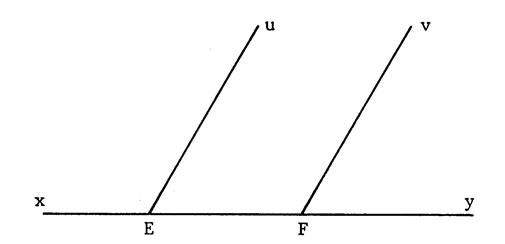
	On donne sur une droite « xy » deux points « E » et « F ». [ Eu et [ Fv sont 2 demi-droites de supports parallèles et situées dans un même demi-plan de frontière « xy ». Tracez [ Ez bissectrice de et [ Ft bissectrice de . Démontrez que [ Ez et [ Ft ont des supports parallèles.

	Hypothèse
	[ Eu // [ Fv [ Eu et [ Fv dans un même demi-plan de frontière « xy ». [ Ez bissectrice de [ Ft bissectrice de .
	Conclusion :

	Démonstration :
	[ Eu et [ Fv étant situé (par hypothèse) dans un même demi-plan de frontière « xy ». Les angles et occupent la position de ………………………..et comme [ Eu // [ Fv ont des supports parallèles, alors , grâce à la propriété ………. ……=….. · Par hypothèse [ Ez est bissectrice de alors ,par définition , · Par hypothèse [ Ft est bissectrice de alors ,par définition , Puisque = alors = donc · occupent la position de …………………… et comme alors , grâce à la propriété ………., [ Fz et [ Fv ont des supports ..parallèles….. .

	Fiche 8 : Somme des angles d’un triangle.			Info +++@ somme des angles dans un triangle.

	Vous avez vu en 5^ème que :
	Propriété 6 : Dans tout triangle , la somme des angles est égale à …180°….

	Activité 1 :
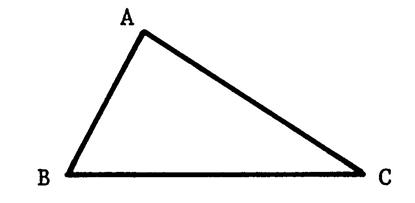
	« ABC » est un triangle tel que : et Calculez la valeur de
	Rappels : - Deux angles dont la somme est de 90° sont dits : ..complémentaires.. - Deux angles dont la somme est de 180° sont dits : ..supplémentaires.. - Dans tout triangle rectangle , les angles autre que l’angle droit sont aigus et …complémentaires..

	Activité 2 :
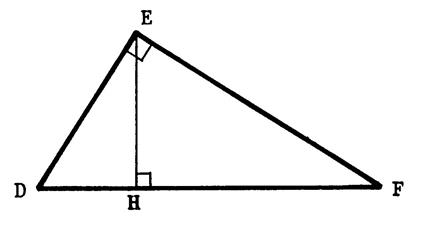
	« DEF » est un triangle rectangle en « E » tel que [ EH ] est la hauteur. Calculez : , , et

	Activité 3 :
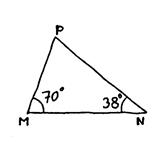
	Dessinez en plus grand le triangle « PNM ».représenté grossièrement ci -contre.
	Le côté [ MN] est déjà placé ci-contre . et Tracez la hauteur [ PK ]. Tracez la bissectrice [ PJ de . Calculez les angles suivants :



	Activité 4 :
	Somme des angles d’un quadrilatère non croisé.			Info ++ sur les quadrilatères…

	Voici ci-contre deux quadrilatères non croisés. Quelle est la somme des angles de chacun de ces quadrilatères. Comment fait-on pour calculer cette somme ? On trace [ FH ] et [ CA ] , pour découper les figures en une somme de deux triangles… ( 180 + 180 = 360° )

CONTROLE:

A voir

EVALUATION: