Pré requis:
|
Tracer une perpendiculaire., une médiatrice , une bissectrice …. |
ENVIRONNEMENT du dossier:
|
Objectif
précédent : Projection d’un point sur une droite |
Objectif
suivant : |
DOSSIER PROJECTION d ' un point sur une droite
perpendiculaire à une droite
donnée.
Dit aussi :
« projection orthogonale »
|
Interdisciplinarité La symétrie
orthogonale |
|
|
|
|
|
|
|
|
Voir définition du mot « direction et
sens ». Mots utilisés dans l’objectif : le vecteur Préambule : La
projection d ’
un point ; d’un segment (un ensemble
de points alignés) implique que l’on doit connaître (ou se fixer) : n une direction (c’est une droite )
n la position du point dans un plan ( en l’occurrence la feuille) et n la droite support qui recevra
le « projeté du point » . |
|
|
|
|
|
||
|
|
|
|
|
|
|
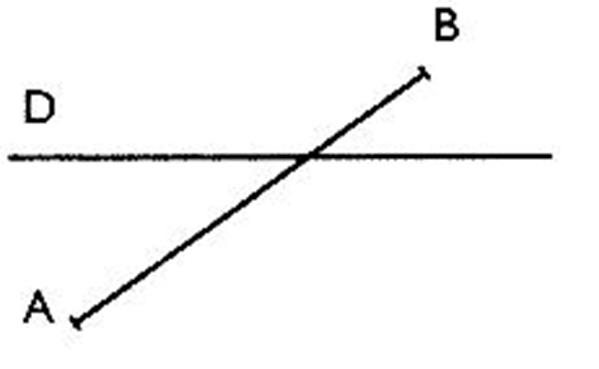
I ) cas
général : Projection d’un
point sur une droite: |
|
|
|
|
|
|
|
|
|
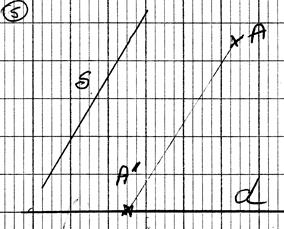
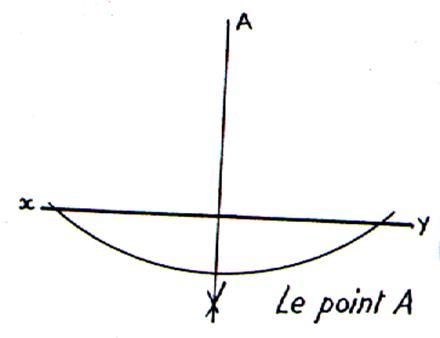
Le point A’ est le projeté du
point A par rapport à la droite
de direction " (le segment de droite AA’ est
parallèle à la droite d), A' se trouve
sur la droite orientée
« axe » . La droite "d" indique la ligne "direction" de
la projetée. |
|
|
|
|
|
|
|
|
|
|
||
|
|
II )
PROJECTION ORTHOGONALE d’un point : |
|
|||||
|
|
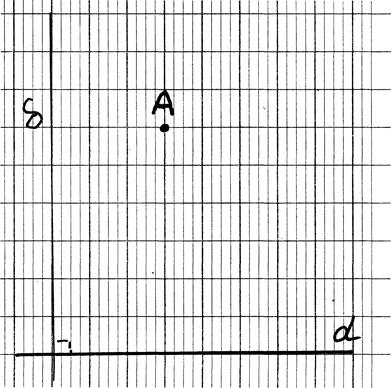
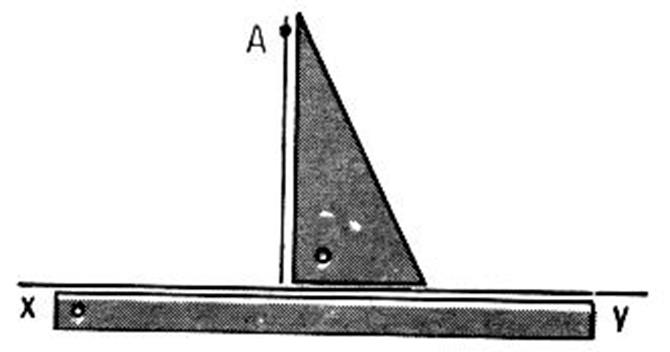
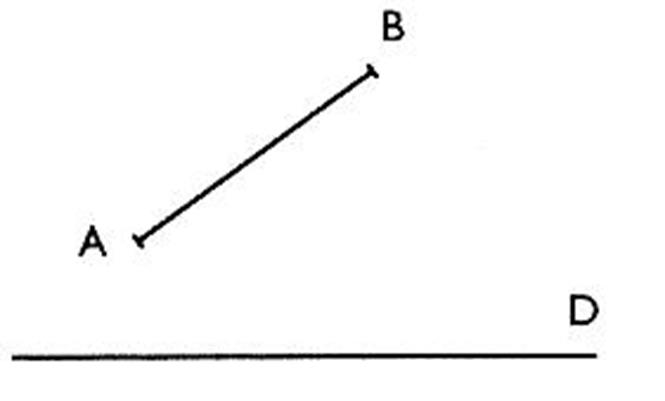
Au départ : On trace un droite « d » , on donne
une droite représentant la direction de projection ( On place un point « A » dans le plan . On demande de tracer la
position du point « A’ » sur « d » , qui sera la projection orthogonale
de « A » sur « d » |
|
|
||||
|
|
|
|
|||||
|
|
On réalise la « projection
orthogonale » d’un point « A » lorsque la direction (delta : |
|
|||||
|
|
|
|
|
||||
|
|
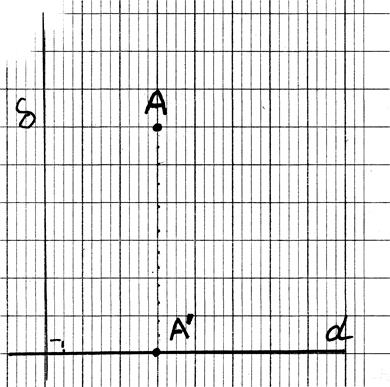
Par définition : Si (d) est perpendiculaire à "d"
et si AA'
est parallèle à "d"
alors A' est le projeté orthogonal de A
sur la droite ( d) ; on
appelle « distance d’un point à une droite » ; la mesure du
segment de droite AA’ portée par un perpendiculaire à la droite « d »
passant par le point « A ». . |
|
|
||||
|
|
|
|
|
||||
|
|
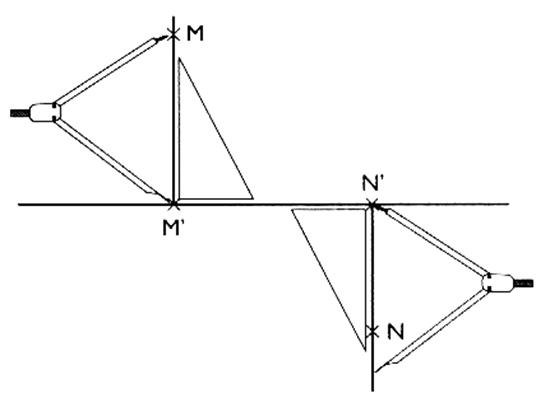
- On
dit : que le
point " A' " est le projeté orthogonal du point "A" sur la droite (D) . - On
dit aussi :
que "A' " est l'image de "A" par la projection
orthogonale dur ( D ). Soit un point
"N" appartenant
à la droite ( D ) , on dira alors que
la projection de "N' " et
le point " N" sont
superposé sur ( D) |
|
|||||
|
|
|
|
|||||
|
|
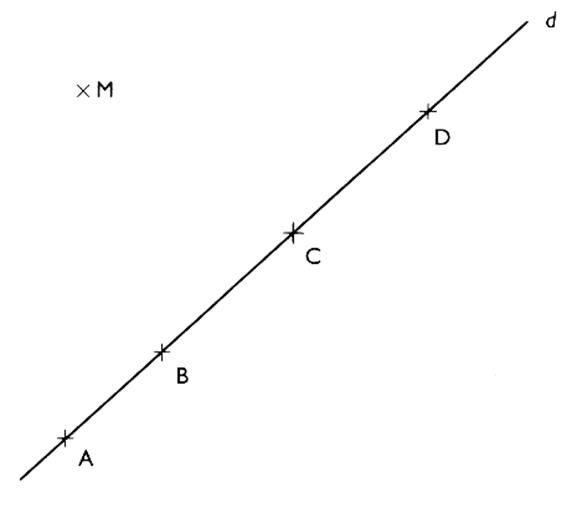
III ) Longueur de la distance du
point M au point M' . Activité : sur une
droite "d" on a placé quatre points. |
|
|||||
|
|
|
|
|||||
|
|
1°) On demande de mesurer les longueurs des
distances séparant ces points. 2°) tracer le projeté orthogonal "M'" de M
sur cette droite "d" . 3°) classer ces 5 longueurs . 4°) Que peut-on dire de la longueur MM' 5°) Peut - on trouver un
autre point de ( d ) qui soit un
distance plus petite ? compléter
la phrase suivante : Sur la droite ( D ) , le
point le plus proche de M est
………………………. Ainsi : La distance entre le point « M » et sa
projeté « M’ » est la distance la plus courte qui sépare ces deux
points. A savoir : la distance la plus courte
entre un point et une droite se mesure sur la droite support de la
projetée orthogonale . Construction
de la projetée orthogonale d'un point
: a) avec
une équerre:
b) avec un compas ( en utilisant
les propriétés de la médiatrice , on peut tracer une perpendiculaire d'un
point extérieur à une droite)
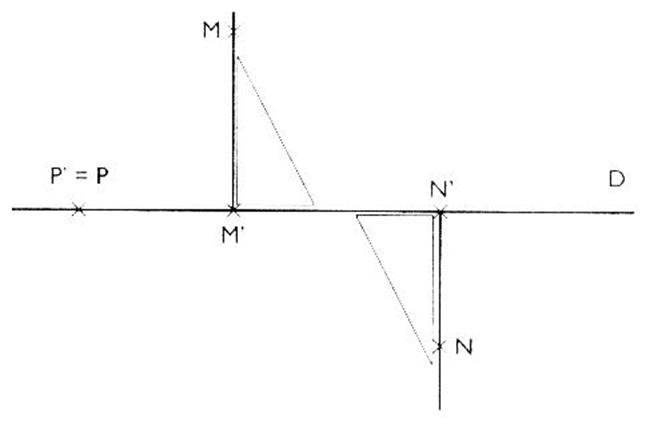
Activité Cours : Construire la projection orthogonale des point M , N et P .
Résultat
: on appellera la projetée de M ® M' ; de N ® N' et de P ® P'.
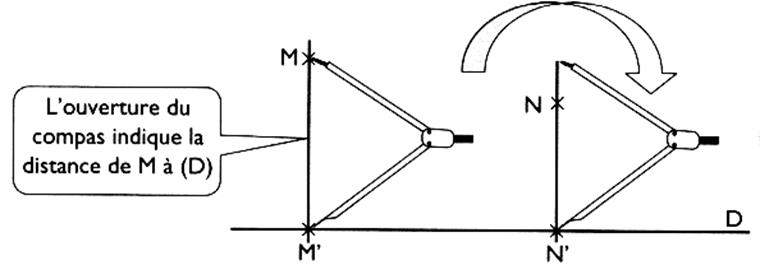
Comparaison de distances : On peut , à partir de la
trace de la projection orthogonale , comparer les distances qui sépare ces
points à l'aide d'un compas .
Projetée
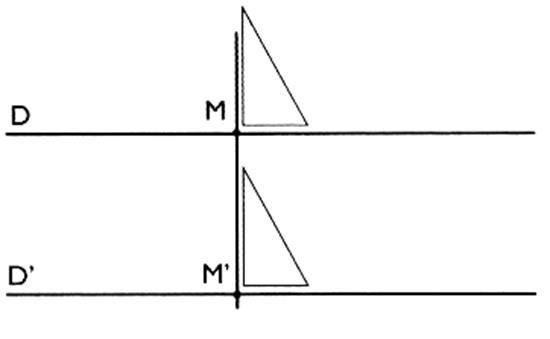
orthogonales et "parallèles": ( cliquer ici : info plus!!) Si les deux
droites des projetées sont du
même côté : et si les points M et N sont
à la même distance de la droite
( D) , on peut tracer ( D ' )
parallèle à ( D)
On peut vérifier
le parallélisme avec une
équerre.
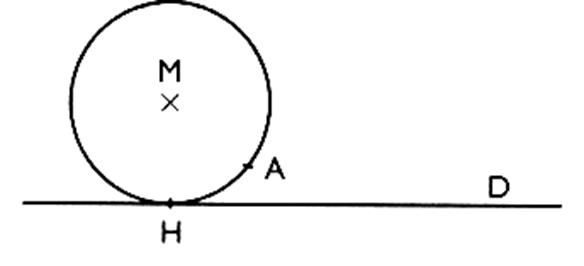
Autre application de la projetée d'un point . Construction
de la tangente à un cercle. Soit un point M et une droite D
. Si je trace la projetée de M sur (D) j'obtient le
point "H"
. Avec un compas je trace un cercle de rayon [MH] ; La droite ( D) peut être
appelée : tangente au cercle .
Domaines
intéressés par la projection
orthogonale : 1.
Les
projections orthogonales 3.
La géométrie descriptive :
l’épure d’un point |
|
|||||
|
|
TRAVAUX AUTO FORMATIFS. |
|
||||||||||
|
|
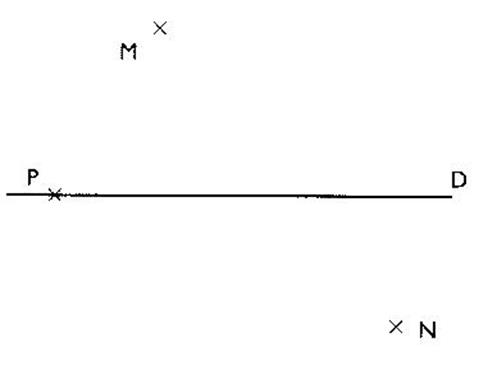
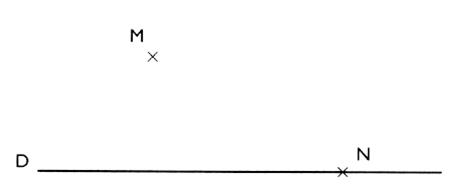
CONTROLE 1°) Pour tracer
la projection orthogonale du point "M" il faut compléter le dessin
par la direction"d" Compléter le
dessin et tracer M' le projeté orthogonal
de M .
EVALUATION
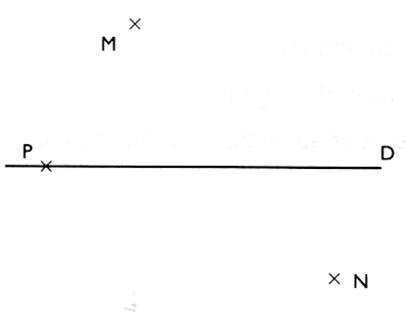
1°) Construire
les projection orthogonales des point M , N et P
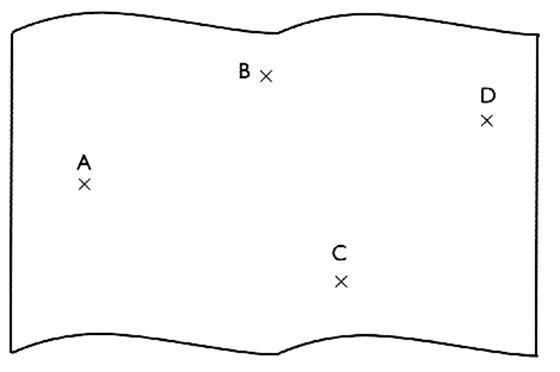
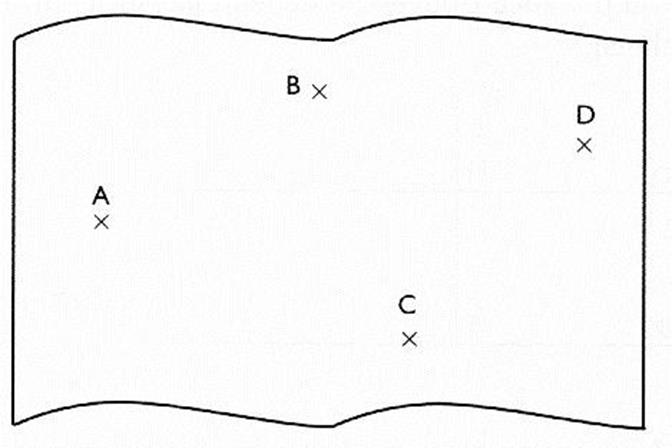
2°) soit quatre
points A ; B ; D ; C a)
tracer une droite passant par AD ; b)
tracer les projetés B' et C'
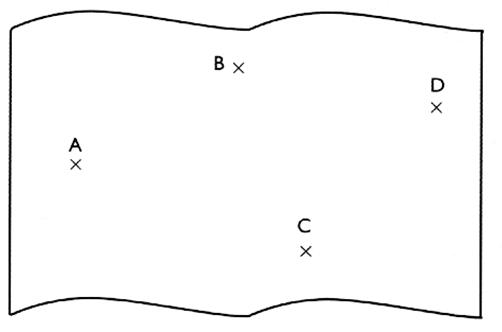
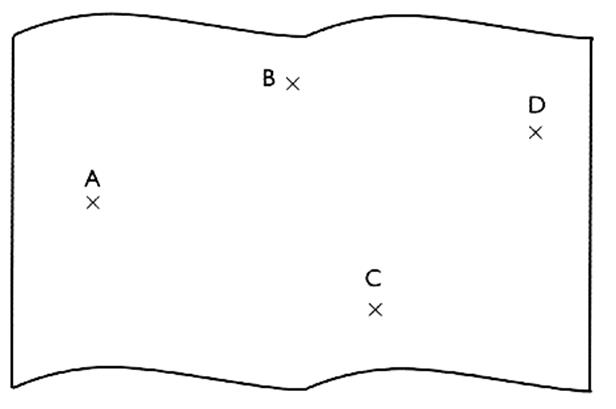
3°) soit quatre
points A ; B ; D ; C a) tracer une
droite passant par CD ; b) tracer les
projetés A ' et B' .
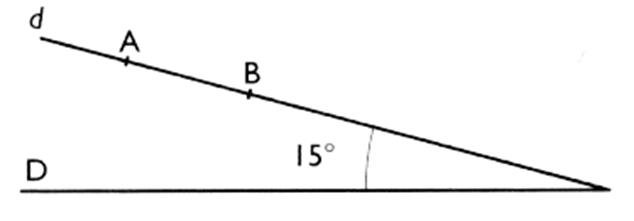
Série
2 1°) Sur la
droite "d" , les deux points A et B sont distants de 5 cm .
Même question
avec des angles de 30° ; 60 ° et 90° ( ce travail sera exploité par "Thalès" et en trigonométrie
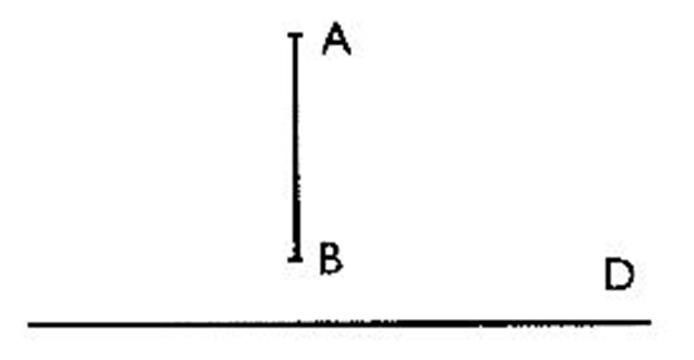
"tangente") 2°) Projection
orthogonale d'un segment sur une droite : a) Reproduire la figure .
Construire A' et B' , projetés
orthogonaux de A et B respectivement
sur ( D) , et tracer [ A ' B' ] : le segment [ A ' B' ] est le projeté
orthogonal du segment [A B] . b) Placer
le point M , milieu de [A B] et construire M' son projeté orthogonal sur ( D )
. Quelle est la position de M' sur [ A ' B' ]
Idem :
Idem :
|
|