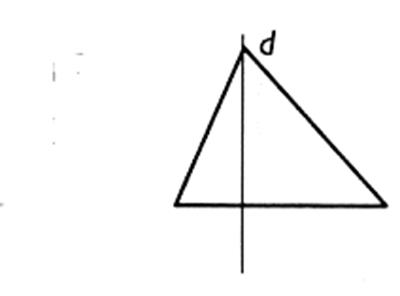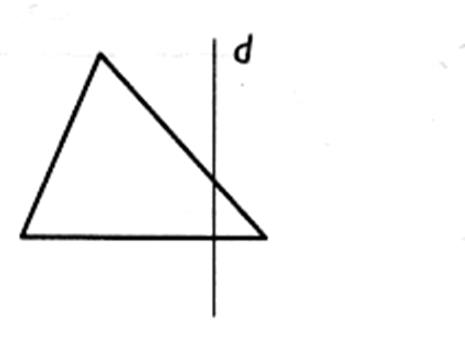|
Niveau
V |
Géométrie : DOSSIER : SYMETRIES / Objectif cours 22 / notation: |
Pré requis:
|
|
|
|
Tracé d’une perpendiculaire à une droite |
|
|
|
|
ENVIRONNEMENT du dossier:
|
1°) L’isométrie et la
rotation axiale et la symétrie
axiale |
Objectif suivant 2°) les
transformations géométriques 3°) Suite
Symétrie orthogonale : de figures simples |
DOSSIER
:
SYMETRIE
ORTHOGONALE ; (dit aussi : symétrie axiale ; ou
« réflexion » )
- Définition
-
Tracé de la symétrie orthogonale d’un point ; d’un segment , d’un triangle
,d’un angle , d’un quadrilatère .
-
Résumé sur les propriétés.
|
TEST |
COURS |
Interdisciplinarité |
|
INFORMATION :
|
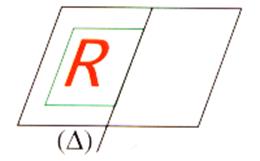
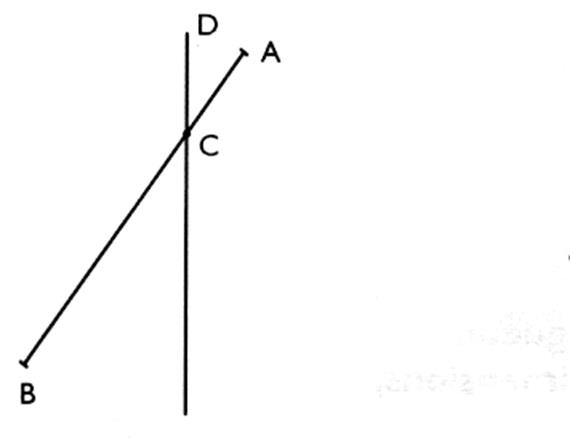
La rotation axiale conduit à la symétrie axiale. Activités : recherche de la symétrie par rapport à
une droite ( delta (D)
) en utilisant la rotation. |
||
|
Dessiner un R (
en rouge) et calquer
ce R ( en bleu) |
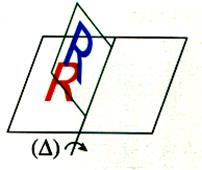
On fait tourner le caque autour de
l’axe (droite) notée (D) |
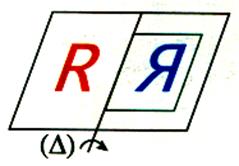
On obtient en bleu le
symétrique de R par rapport à la
droite (D) |
|
|
|
|
Rappels sur les tracés d'une perpendiculaire à une
droite passant par un point donné:
|
Avec l'équerre !!!!!! |
Avec le compas !!!! |
|
|
|
|
|
|
|
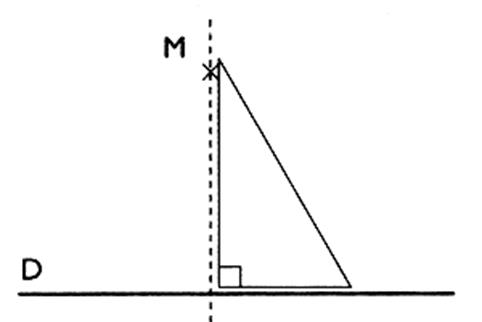
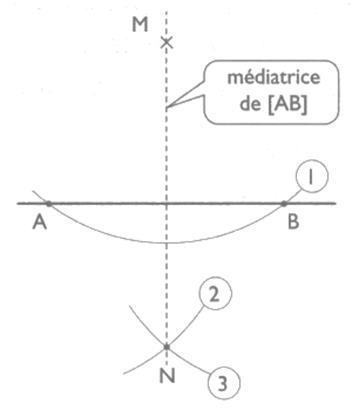
Construction du symétrique d’un point par rapport à
une droite .
II
) SYMETRIE ORTHOGONALE DE DEUX POINTS.
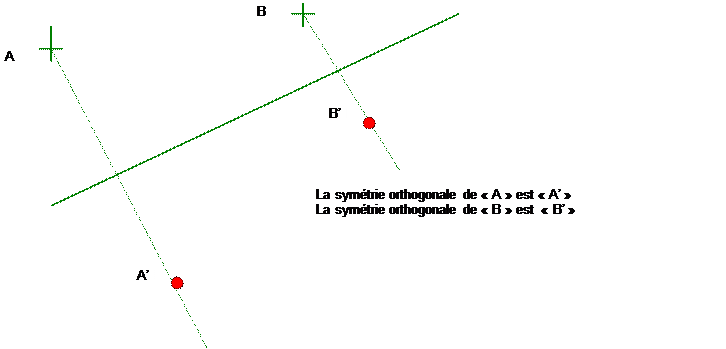
III) SYMETRIE
ORTHOGONALE D’UN SEGMENT :
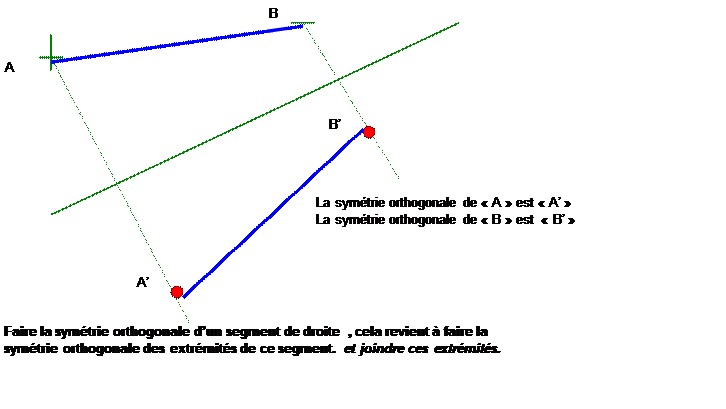
IV
) SYMETRIE ORTHOGONALE D’UN
TRIANGLE :
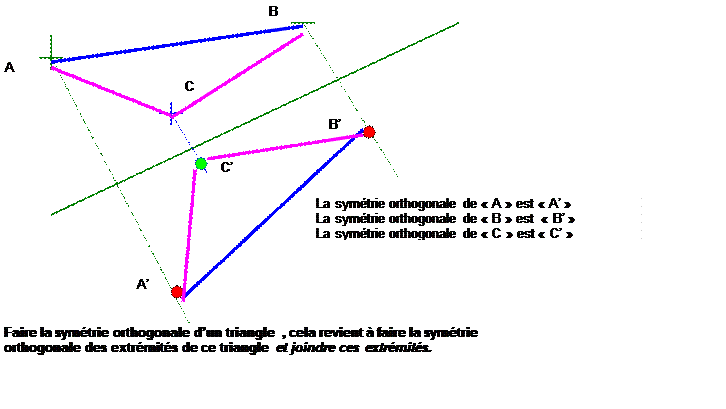
V ) SYMETRIE
ORTHOGONALE D’UN ANGLE :
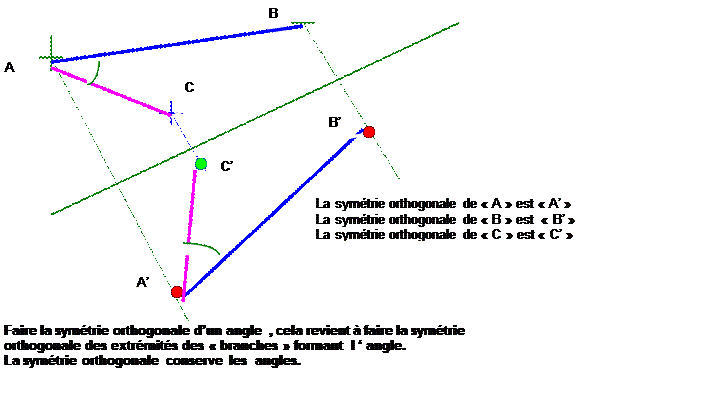
VI ) SYMETRIE ORTHOGONALE D’UN QUADRILATERE :
Faire
la symétrie orthogonale d’un quadrilatère , cela revient à faire la symétrie
orthogonale des extrémités de ce quadrilatère et ensuite joindre ses extrémités.
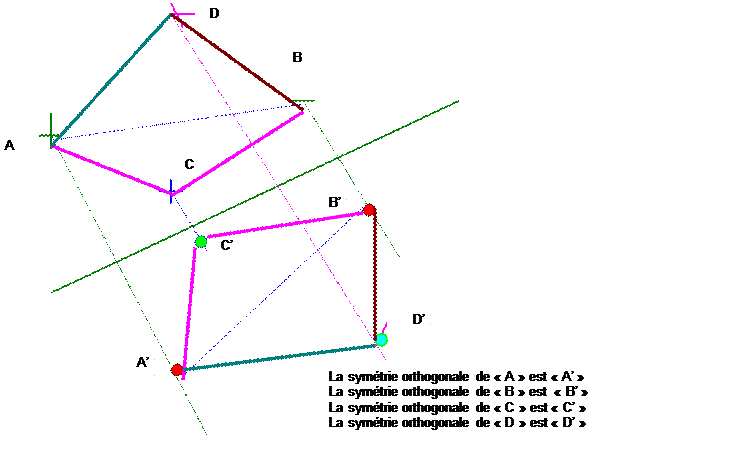
Et ainsi de suite :
C ) EN
RESUME :
Dans une symétrie orthogonale par rapport à une droite , cette droite est appelée "axe de symétrie"
Si un point est sur l'axe se
symétrie alors l'image de ce point est ce point lui même.
Il en est de même pour tout point
appartenant à l'axe . Nous dirons que l'axe de symétrie est
"invariant" dans la symétrie
par rapport à son axe.
|
Comme dans la
symétrie centrale : |
Dans la Symétrie orthogonale de figures simples:
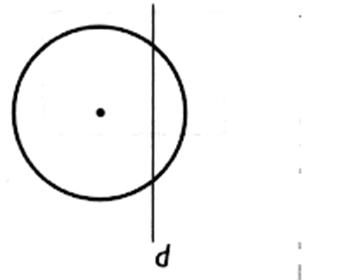
L'image d'un cercle
est un cercle de même rayon.
Donc : l'image d'un disque est un
disque de même aire.
L'image d'un triangle est un triangle de mêmes
dimensions
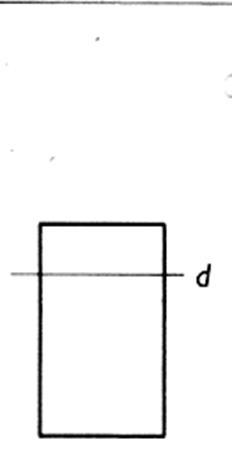
L'image d'un rectangle est un rectangle de mêmes
dimensions
L'image d'un carré est un carré de mêmes dimensions
L'image d'une figure quelconque est une figure
quelconque de mêmes dimensions
EN CONCLUSION:
|
Une symétrie orthogonale conserve : L'alignement Les longueurs Les angles Il en résulte que toutes figures
géométriques à pour image une figure de mêmes dimensions , donc de
même aire. Une symétrie orthogonale
conserve aussi : les aires . |
|
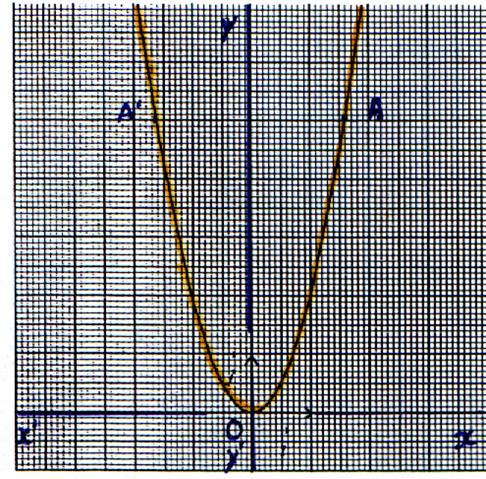
Exemple appliqué aux études de fonction : L’axe « y’ y » est axe de symétrie
dans le tracé de la fonction « x2 » Les points
A’ et A sont symétrique par rapport à « y’y »! ! |
|
|
|
TRAVAUX
AUTO FORMATIFS |
|
||||||
|
|
CONTROLE A savoir : Une symétrie
orthogonale conserve : L'alignement Les longueurs Les angles |
|
||||||
|
|
SERIE 1 : 1°) Placer un point "A" à une distance de
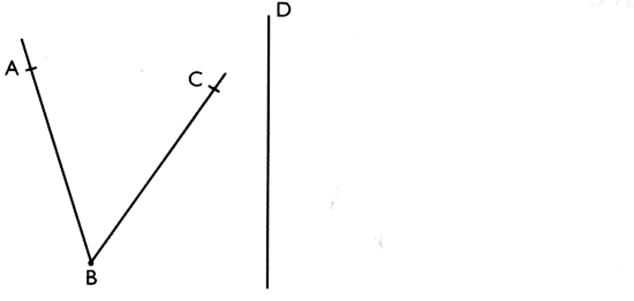
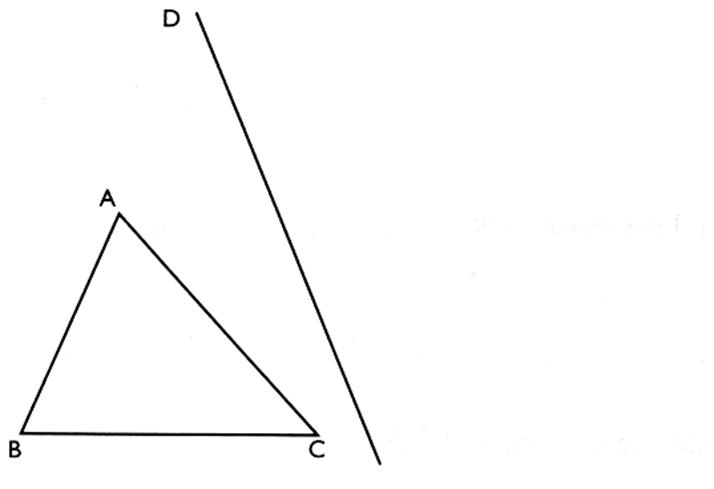
2°) Construire le symétrique de l'angle par
rapport à la droite ( D )
4°) Construire le symétrique du polygone par rapport
à la droite ( D )
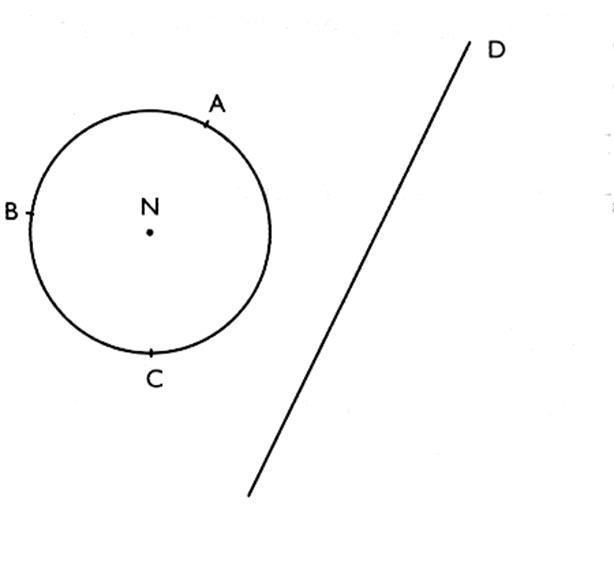
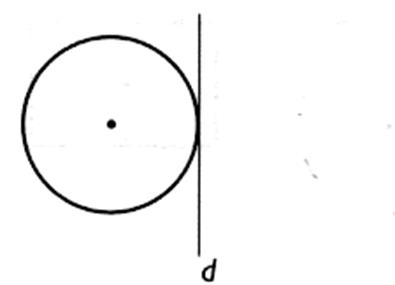
5°) Construire le symétrique du cercle par rapport
à la droite ( D )
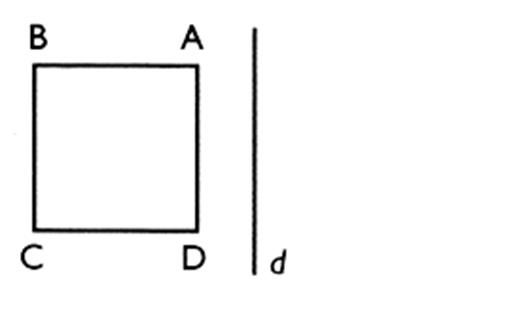
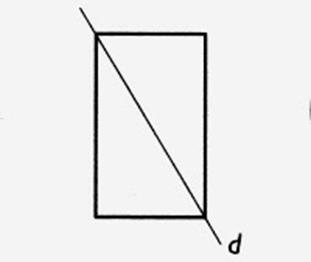
6°) Construire le symétrique du polygone par rapport
à la droite ( d )
SERIE 2 : 1°) Construire le symétrique [ A'B'] du segment AB de longueur Vérifier que I' est le milieu de [ A'B'] . On dit que la symétrie orthogonale conserve le
milieu . [ A'B']
2°)
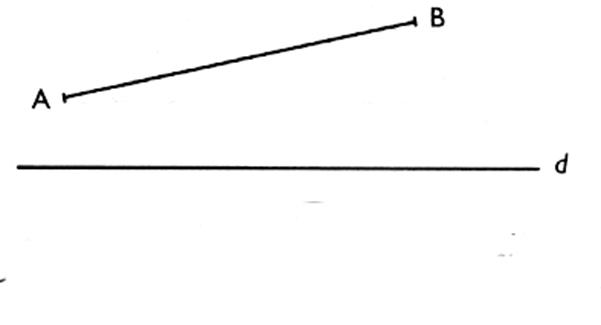
Construire le symétrique du segment AB par rapport à la droite
( D )
3°) Construire la symétrique de la figure ci-
dessous par rapport à la droite "D" .
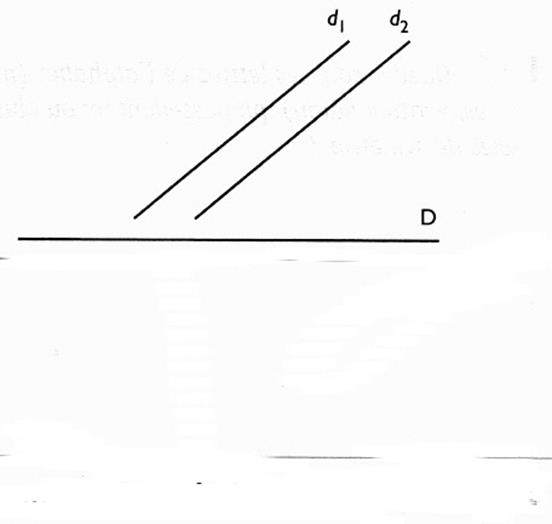
4°) Construire la symétrique des figures ci- dessous par rapport à la droite
"d"
|
|