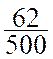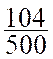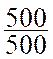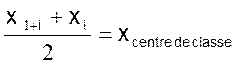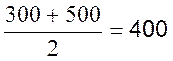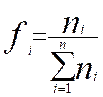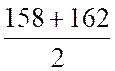COURS N°

I )  Notion  "d’effectif" et de "fréquence" :

Dans un tableau statistique on trouve souvent plusieurs colonnes : dont une dans laquelle on trouve des nombres  que l’on appelle  « les effectifs » et une autre des valeurs numériques que l’on appelle  « les fréquences ».

Exemple :   Nous partons  d’un premier tableau de données  ,établi suite à une étude statistique (sondage) :

La série statistique représente 500 automobiles classées dans un parc d’après leur marque ; (regroupée dans le tableau ci-dessous) :

On décide de présenter autrement le tableau ci-dessus  .

Considérons la série statistique qui représente 500 automobiles classées dans un parc d’après leur marque . L’unité statistique est ici une automobile , le caractère  (ou la variable)  qualitative est la marque de l’automobile . Un état de la variable ou une valeur de la variable est le « nom de la marque » : « Renault , Peugeot … » .L’effectif d’une marque « n_i » d’automobiles ayant cette

marque . Ainsi , l’effectif des voitures de marque Renault est 18O . L’effectif total de la population est 500.

       Dans la deuxième colonne d’un tableau  statistique  on enregistre   le nombre de fois que la valeur de la variable,( mentionnée dans la première  colonne ) , a été  rencontrée .

Cette deuxième colonne est appelée : colonne des effectifs noté « n_i ».

   Définitions :

1°) l’effectif  , comme son nom l’indique , donne le nombre d’unités en valeurs absolues , il est noté n_i , c’est une fréquence absolue .

2°) La fréquence d’une modalité de la variable est le rapport de l’effectif correspondant à l’effectif total de la population . Ce rapport est noté  « f_i » 

2°) Calcul de  L’effectif total  ( noté :   N _i  )    :  

N _i  =  )

ce qui doit se traduire par la phrase : l’effectif total  est égal  à la somme des effectifs

Exemple :  Dans ce tableau on a calculé l’effectif total , la fréquence par « caractère » et on a exprimé chaque fréquence en pourcentage.

On remarquera que  pour un effectif total des caractères  : la somme des fréquences est égale à « 1 » et que la somme des pourcentages est égale à 100 %.

II  )   L’ EFFECTIF : (simple et total)

Par définition :

Effectif simple ( noté :n _i )   : (cette valeur est donnée)

 L’effectif d’une valeur de la variable statistique (caractère ou classe) est le nombre d’unités statistiques qui possèdent cette valeur , cet effectif est appelé :effectif simple ».

Effectif total : ( noté N )     (cette valeur est calculée)

L’effectif total d’une population statistique est le nombre total d’unités statistiques. C’est la somme des effectifs simples.

Nombre d’enfants

x _i

Effectif

n_i

L’effectif total est égal à la somme :

8 + 35 + 39 + 15 +4 + 1  = 102

N = 102

0

 8

1

35

2

39

3

15

4

  4

5 et +

  1

N=

102

Exemple 2 :

   On donne dans le tableau un effectif par classe   (Tableau concernant une variable continue).

· L'  effectif par « classe »  est un "sous- effectif" on le note  petit  " n " avec un indice d'ordre  :

· On calculera  L' effectif total est la somme des éléments qui sont inventoriés . « nombre d’entreprises » 

Distribution  du chiffre d’affaires  ( C. A.)  déclaré  par les entreprises de distribution d’une chaîne de magasin.

C.A.   .(milliers d’euros )

                  x _i

Effectifs

(  n _i )

L’effectif total est égal à la somme :

22 + 25 + 90 + 33  +24 + 6  = 200

N = 200

300 à moins  500

22

500 à moins  800

25

800 à moins  1 000

90

1 000 à moins 1400

33

1 400 à moins  1500

24

1500 et +

  6

N =

     200

III ) Remarques sur : « classe » , « classe modale », « centre de classe ».

Conclusion : · dans un tableau on donne  L'  effectif par « classe »  (qui est un "sous- effectif" )  ou un effectif par « caractère » . cet effectif par classe ou caractère est noté par le  petit  " n " avec un indice d'ordre  : les   (n _i ) 

· On calculera  L' effectif total est la somme des éléments (n _i )  qui sont inventoriés . Le symbole désignant l'effectif total est  " N "

Lorsque le caractère est dit « continu » , ses éléments sont regroupés dans des « sous effectifs » que l’on appelle : Classe.

Rappel : « Classe modale » :

    On appelle  « classe modale » la classe qui possède le plus grand effectif .

C.A.

(milliers d’euros )

     x _i

Effectifs

(  n _i )

L’effectif «  n ₃ » de la classe «  x ₃ » étant le plus grand .

La classe « x ₃ »  est la classe « modale » ;

    x ₁ =300 à moins  500

22

    x ₂ = 500 à moins  800

25

    x ₃ = 800 à moins  1 000

 n _{3  =}  90

    x ₄ = 1 000 à moins 1400

33

    x ₅ = 1 400 à moins  1500

24

     x ₆ = 1500 et +

  6

Remarques :

► pour tracer le polygone des effectifs  ou fréquences, il faudra rechercher pour chaque classe observée : « son centre de classe » .appelé aussi : « moyenne de centre de classe » ou « valeur centrale d’une classe ».

► Dans le calcul de l’écart type  , on prendra la valeur centrale de chaque classe comme « x _i »

« Valeur centrale » d’une classe. : la valeur centrale est la valeur médiane de la classe.(calcul d’une moyenne)

Soit la classe :    [x _i ; x _i+1 [  , la valeur centrale sera le  Centre de classe :  x _icentrale

Classe :

Valeur centrale :

[ 300 ; 500[

On se souviendra que dans les calculs de l’écart type on « admet que les valeurs observées sont celles du centre de la classe ».

« Classe » et « amplitude »

La représentation graphique des effectifs d’une variable continue ( organisation de « classe » pour ranger ces effectifs)peut s’effectuer sous la forme d’un histogramme.

Pour respecter le principe de construction de l’histogramme, on devra veiller à vérifier que les intervalles  de toutes les classes sont égaux.

, On dit que les clases doivent avoir la même amplitude.

Exemples :

Classes d’amplitudes inégales

Classe d’amplitudes égales

[ 300 ; 500[

Cette série ne sera pas exploitable pour tracer un histogramme. Il faudra repenser la distribution.    Voir « l’informaticien ».

[ 300 ; 500[

Cette série est exploitable pour tracer un histogramme.

[ 500 ; 800[

[ 500 ; 700[

[ 800 ; 1000[

[ 700 ; 900[

[ 1000 ; 1400[

[ 900 ; 1100[

[ 1400 ; 1500[

[ 1100 ; 1300[

????

[ 1300 ; 1500[

IV ) FREQUENCE :

Comme nous l’avons vu au chapitre 1 : la fréquence est une autre façon d’exprimer la valeur d’un effectif (par caractère ou par classe)  par rapport à l’effectif total (somme des effectifs ).

Il y a deux façons d’exprimer une fréquence .

La fréquence peut être un nombre décimal  (inférieur à 1 ) ou la fréquence peut être exprimée sous la forme d’un pourcentage ( a%)

Dans un problème ,on vous précise sous qu’elle forme on doit exprimer cette fréquence.

Mais dans tous les cas :

• Si la fréquence est exprimée sous forme décimale : la somme des fréquence sera égale à 1
• Si la fréquence est exprimée sous d’un pourcentage  : la somme des fréquence sera égale à 100 %

Ainsi :  Pour calculer la fréquence il faut connaître l’effectif de  la  valeur  observée   par « caractère »  ou l’effectif par « classe » et l’effectif total de la série étudiée .

On dira que la fréquence d’une modalité de la variable est le rapport de l’effectif correspondant à l’ effectif total de la population. Ce rapport est noté :  f _i

ge

Les mesures sont des observations qui informent :( VOIR EXEMPLE précédent ? ? ? ?° ):

Des valeurs précédentes nous établissons le tableau suivant : (calcul des valeurs centrales et calcul des fréquences )

Commentaire :

En opérant le regroupement en intervalles, nous avons constitué 7 classes.

Dans chaque classe , les effectifs montrent le nombre d'événements produits  (l' événement est : taille - individu).

Si nous divisons l'effectif de chaque classe par le nombre de mesures (30), nous obtenons la

" Fréquence" de chaque classe.

Exemple :

Par définition : La fréquence d’une valeur de la variable statistique est le rapport de l’effectif de cette valeur à l’effectif total.

V)   Effectif simple  ( n_i ) et  effectif cumulé ( N_i )  et

     Fréquence simple  ( f_i )  et fréquence cumulée ( F_i )

Info ++

1°) L’effectif simple et les fréquences simples  indiquent comment se distribue la variable  par rapport aux différentes modalités .

2°) l’effectif cumulé et les fréquences cumulées  indiquent  comment se répartit la variable par rapport  aux différentes modalités .

il existe par ailleurs deux catégories  de fréquences cumulées  :

- les fréquences cumulées croissantes qui indiquent combien d'unités de la population sont caractérisées par une valeur inférieure à ……;

- les fréquences cumulées décroissantes  qui indiquent combien d'unités de la population sont caractérisées par un valeur supérieure à ……

exemple : soit un premier tableau représentant la distribution du chiffre d'affaires  ( C.A. )déclarés par les magasins d'un réseau de distribution d'une marque de textile .