|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent |
Objectif
suivant : |
DOSSIER : Les HISTOGRAMMES
|
|
1 °) Définition |
|
|
|
2 °)
- Construction d’un histogramme . |
|
|
|
3 °)
Représentations graphiques : applications. |
|
|
|
4 °)
Exercice résolu : . |
|
|
|
5 °) voir
une situation problème sur la gestion de données (5ème
collège)….. |
|
|
|
|
|
|
|
|
||
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 – Définition |
|
|
Le graphique |
Est utilisé pour représenter : |
C'est-à-dire (schématiquement ) : |
|
HISTOGRAMME |
Une série statistique dont les valeurs sont regroupées en classe . |
|
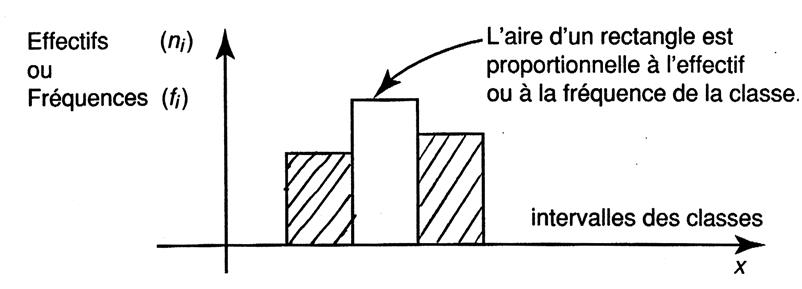
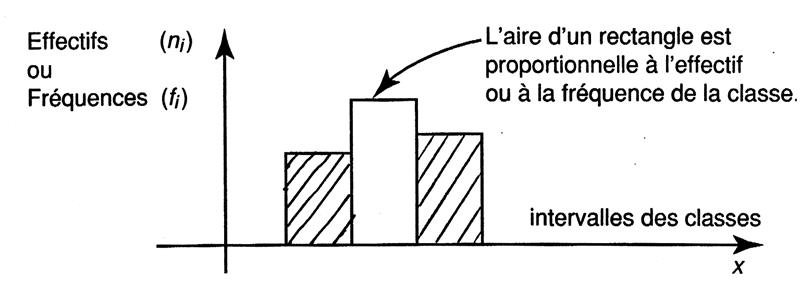
Un histogramme est constitué d’une succession de rectangles accolés .
|
Lorsque
les valeurs prises par un caractère statistique sont regroupées en classes ,
on les représente par un histogramme. |
|
L’aire de chaque
« rectangle » est proportionnelle à l’effectif ou la
fréquence associé (e).
|
Il est nécessaire que les rectangles aient la même largeur . On dit que les classes ont toutes la même amplitude . |
Que représente un histogramme ?
Réponse :
L’histogramme sert à représenter uniquement les séries à caractère quantitatif continu . ( effectifs ou fréquences)
C'est à dire que lorsque les valeurs prises par le caractère sont
regroupées en classes : on porte en
abscisse les limites des classes .
En ordonnée on peut représenter :
·
Les effectifs ( n i ) :
'effectif d'une classe est représenté par un rectangle dont l'aire est
proportionnelle à l'effectif de la classe . ( les rectangles sont
"accolés" )
·
Les fréquences : de chaque
classe .
On retiendra en
résumé que :
|
Le graphique |
Est utilisé pour représenter : |
C'est-à-dire (schématiquement ) : |
|
HISTOGRAMME |
Une série statistique dont les valeurs sont regroupées en classe . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 -
Construction d’un histogramme . |
|
|||||||||||
|
|
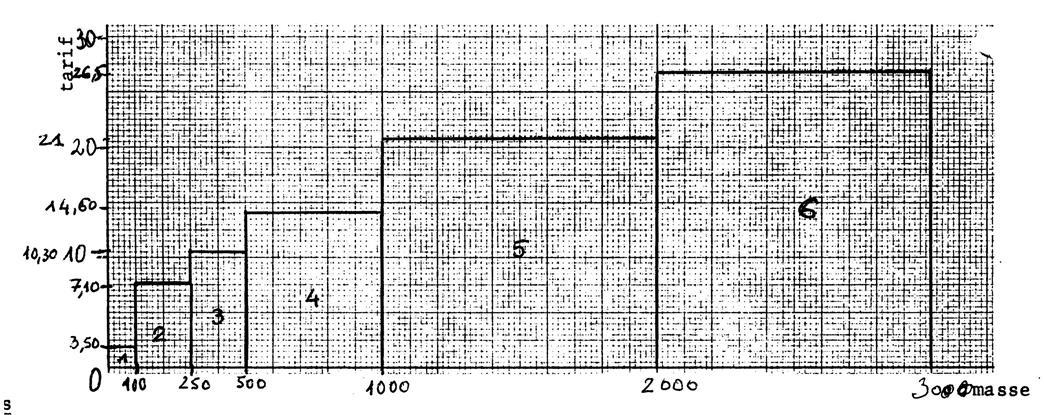
Le tableau ci-dessous donne les tarifs exigés pour le transport des
paquets-poste contenant des objets fragiles
en fonction le leur masse
(jusqu’à 3 000 grammes ,(« gramme » pour
lettre « g » ). La lettre « m » désigne la masse du paquet en « g » . |
|
|||||||||||
|
|
Masse
en «g » |
m |
100 |
250 |
500 |
1000 |
2000 |
|
|
|
|||
|
Tarif
en « € » |
3,50 |
7,10 |
10,30 |
14,60 |
21,00 |
26,50 |
|
|
|||||
|
|
|
|
|||||||||||
|
|
On vous demande de faire la représentation graphique correspondante. |
|
|||||||||||
|
|
Conseil :
commencez par choisir convenablement les unités sur les axes. (voir info cours précédent
sur le repérage et les graduations ).afin d’utiliser au maximum les
graduations des axes tracés ci-dessous. |
|
|||||||||||
|
|
Attention :
Le graphique que vous devez dessiner est différent de ceux que vous avez
faits jusqu’à ce jour. Vous
n’allez pas obtenir une courbe continue mais une succession de segments disposés
en escalier. |
|
|||||||||||
|
|
Exemple : Entre « 1 000 g »
et « 2 000g » , le tarif est
de 21 € , c’est-à-dire que pour une paquet de 1150g ; 1550 g ; 1875
g (par exemple)le tarif est de 21 €. Les points correspondants ont donc « la même ordonnée ». Ils sont donc situés sur un segment parallèle à l’axe des abscisses. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Corrigé :
|
|
|||||||||||
|
|
Questions : |
|
|||||||||||
|
|
1°) Le tarif d’affranchissement est –il proportionnel à la masse du paquet ? ……NON…. 2°) Quel est le tarif pour : |
|
|||||||||||
|
|
135
g = ………7,10……€ |
730
g = ……14,60……€ |
2,650
g = ……26,50…….€ |
|
|||||||||
|
|
|
|
|||||||||||
|
|
3°) On dispose de 18 € pour
payer le transport d’un paquet. Quelle est la masse maximum du paquet que l’on peut expédier ? ……1 000 g …. |
|
|||||||||||
|
|
4°) On veut expédier à une même personne 2 objets pesant chacun « 100 g » ( emballage compris). Pour que le prix soit le moins élevé possible, doit-on faire un paquet
ou deux paquets ? (expliquez) 2 paquets par ce que un paquet peut être inférieur ou égal à 100
g.et qu’un objet pèse 100 g . |
|
|||||||||||
|
|
5°) On veut expédier à une même personne 6 objets pesant chacun 100 g ( emballage compris)
. Pour que le prix soit le moins élevé possible doit-on faire un ou plusieurs
paquets ? (
expliquez) . |
|
|||||||||||
|
|
En testant toutes les solutions
on fera : Le colis fait 600g : le cout de ce paquet est de 14,60 € |
|
|||||||||||
|
|
6°) Même question pour 6 objets pesant chacun 200 g
. |
|
|||||||||||
|
|
Il en est de même : 6 fois 200 = 1200 g ; le coût sera de 21 € |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
3 – Représentations graphiques :
applications. |
|
|||||||||||
|
|
Attention : un histogramme est une représentation par une surface . L’ échelle doit être indiquée par une
surface ( carré ou rectangle ) et l’ Oy ne représente aucune grandeur
concrète : écrire « effectif » sur cet axe et le graduer est
donc une faute grave , bien que courante et entretenue par la confusion avec
un diagramme en tuyaux d’orgue. |
|
|||||||||||
|
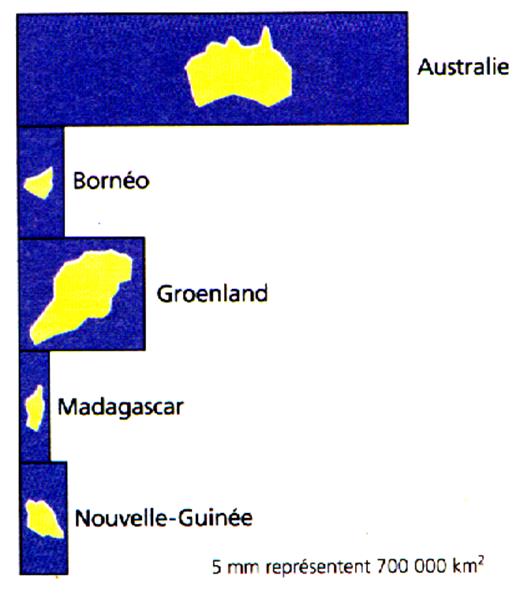
Commentez
les dessins présentés : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 – Exercice
résolu : . |
|
On a
relevé les moyennes des notes des 30 élèves d'une classe d'un établissement
scolaire. Les résultats sont regroupés dans le tableau ci-dessous:
|
Moyenne |
Effectif |
|
[ 7 ; 9 [ |
7 |
|
[ 9 ; 11 [ |
9 |
|
[ 11; 13 [ |
3 |
|
[ 13 ; 15 [ |
6 |
|
[ 15 ; 17[ |
5 |
On demande :
1°) quel est le caractère observé ? Est - il qualitatif ou quantitatif
? Pourquoi a - t - on effectué un regroupement en classes ?
2°) Quelle est la moyenne la plus petite et la
plus grande obtenue.
3°)
Construire l’histogramme de cette série statistique :
Pour ce faire on
prend
Solution :
1°) Le caractère observé est la note
moyenne .Elle est quantitative puisqu'il s'exprime par des nombres.
On effectue un regroupement en classes parce que les valeurs sont
quelconques .
2°) la moyenne la plus petite obtenue
est "7" et la plus grande est "17"
3°)Construction de l’histogramme de cette série
statistique:
Recherche des hauteurs :
|
Note |
Effectif . |
Calculs des
hauteur des rectangles |
|
[ 7 ; 9 [ |
7 |
|
|
[ 9 ; 11 [ |
9 |
|
|
[ 11; 13 [ |
3 |
|
|
[ 13 ; 15 [ |
6 |
|
|
[ 15 ; 17[ |
5 |
|
Représentation graphique :
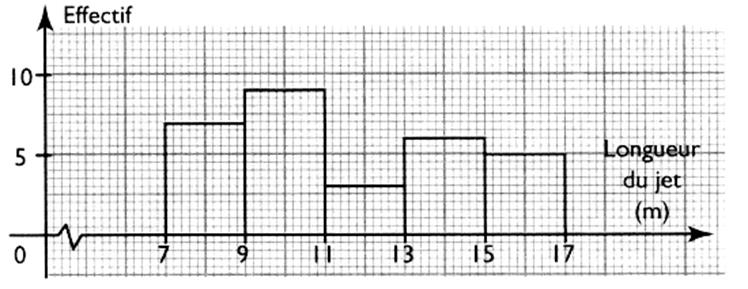
Autre exercice :
|
|
|
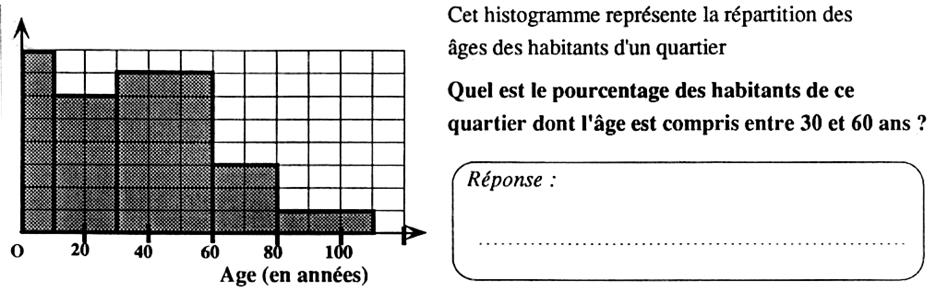
Réponse : 42 % |
|
|
|
|||||||
|
|
Organisation et gestion de données. (histogramme ) |
corrigé
(allez à la fiche n°7) remarque : vous verrez dans le corrigé que ce même problème peut être « à
réaliser » par le diagramme circulaire. |
||||||
|
|
|
|||||||
|
|
Dans une société comportant
« 1300 » salariés , on a voulu se rendre compte de la
répartition des âges des salariés . Pour cela, on a constitué « 6 » tranches d’âge et on a
compté combien il y avait de personnes dans chaque tranche. Ensuite, on a calculé la fraction du nombre total de salariés
correspondant à chaque tranche. On a obtenu le tableau ci-dessous
. ( la lettre « A » désigne l’âge.) |
|||||||
|
|
|
|||||||
|
|
Tranche d’âge |
A < 20 |
20 |
30 |
40 |
50 |
60 |
|
|
Nombre
de salariés |
104 |
|
|
|
|
|
||
|
Fraction |
|
|
|
|
|
|
||
|
Pourcentage
|
8 % |
|
|
|
|
|
||
|
Angle. |
28,8° |
|
|
|
|
|
||
|
|
|
|||||||
|
|
1°) La ligne du tableau donnant le nombre de salariés par tranche a
été effacée, on vous demande de la compléter . |
|||||||
|
|
Exemple de
calcul :
pour la tranche des moins de 20 ans , la fraction du nombre total est
de le nombre de
moins de vingt ans est donc : |
|||||||
|
|
|
|||||||
|
|
2°) Calculez le pourcentage correspondant à chaque tranche d’âge. |
|||||||
|
|
Exemple de
calcul : pour
la tranche des moins de vingt ans on
pose : |
|||||||
|
|
|
|||||||
|
|
3°) Faite l’histogramme représentant le nombre de salariés
correspondant à chaque tranche d’âge . ( voir ci-dessous les axes de coordonnées .)n |
|||||||
|
|
|
|||||||
CONTROLE :
Que représente un histogramme
? (dites ce qui le caractérise)
Dans
un histogramme qu’est ce qui doit - être
proportionnel au effectifs ?
EVALUATION
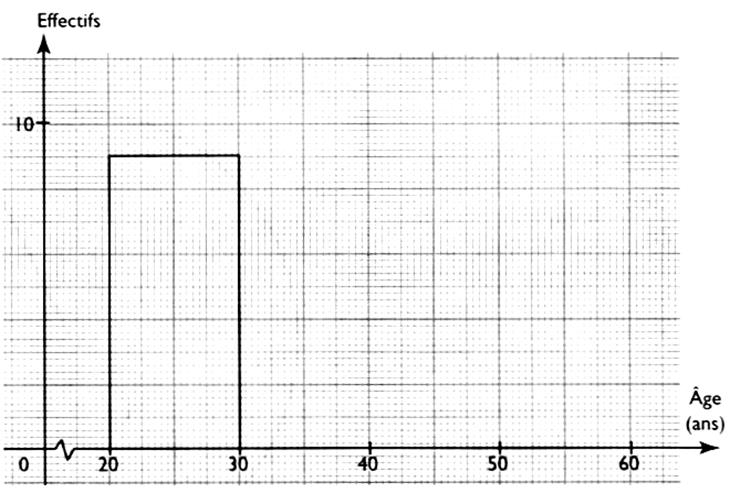
1°) Donner une représentation
graphique d’un histogramme .
A partir de l'histogramme ,
compléter le tableau suivant:
|
Classe |
Effectif |
|
[ 0 ; 100 [ |
|
|
[ 100 ; 200 [ |
|
|
[ 200 ; 300 [ |
|
|
[ 300 ; 400 [ |
|
|
[ 400 ; 500 [ |
|
|
Total
|
|
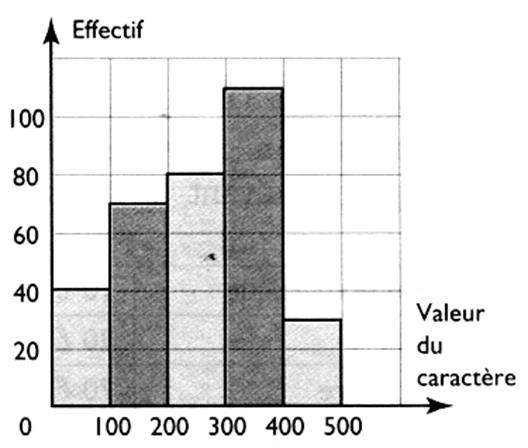
2) Au cours d'un examen , les 40 candidats ont obtenu les résultats
suivants :
15 - 1 - 6 -13 -15 - 1 8 - 10 - 18 - 11-14-14- 5-6-9- 15-12-17 - 7-2-17-
1-9-8 -18 - 5 - 15 - 13 - 6 - 8 - 10 - 16 - 11 - 9 - 11 - 13 - 12 - 6 - 14 - 10 .
1°) Répartir ces résultats dans des classes d'amplitude "5" :
[0; 5 [ ; [5 ; 10 [; ..etc.
2°) dresser un tableau. (comme ci dessous )
|
Classe : |
Effectif |
|
[0; 5 [ |
|
|
…….. |
|
|
Total
: |
|
3°) construire un histogramme .
On a
relevé les moyennes des notes des 30 élèves d'une classe d'un établissement
scolaire. Les résultats sont regroupés dans le tableau ci-dessous:
|
Moyenne |
Effectif |
|
[ 7 ; 9 [ |
7 |
|
[ 9 ; 11 [ |
9 |
|
[ 11; 13 [ |
3 |
|
[ 13 ; 15 [ |
6 |
|
[ 15 ; 17[ |
5 |
On demande :
1°) quel est le caractère observé ? Est - il qualitatif ou quantitatif
? Pourquoi a - t - on effectué un regroupement en classes ?
2°) Quelle est la moyenne la plus petite et la
plus grande obtenue.
3°)
Construire l’histogramme de cette série statistique :
Voir les livres de géographie .
corrigé CONTROLE :
Qu’est qu’un histogramme ?
corrigé
EVALUATION
Donner une représentation
graphique d’un histogramme .
corrigé INTERDISCIPLINARITE
Voir les livres de géographie .