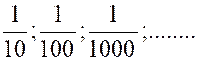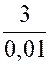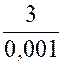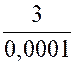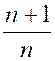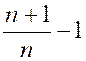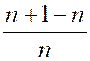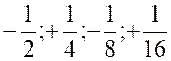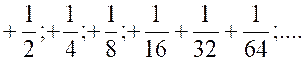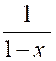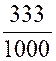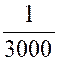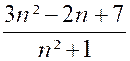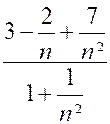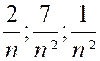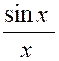Chapitres

1.      Quantité infiniment petite.

2.    Quantité infinie.

3.     « LIMITE » : quelques exemples (9)

4.   Remarques ( 3)

5.   Principe fondamental.

Pré requis  à : … l’étude de formes  particulières . Il arrive quelque fois qu’une fraction , pour certaines valeurs particulières assignés aux lettres qu’elle contient , voit s’annuler son numérateur ou son dénominateur ou même l’un et l’autre , et prend une des formes : «  » ; «  » ; «  » .

Nous allons chercher le sens de ces formes singulières , après s’être imprégné des notions sur l’infini et sur ces limites.

1°)  Quantité infiniment petite.

On appelle « quantité infiniment petite » une quantité variable décroissant indéfiniment, en valeur absolue , de façon à devenir définirivement moindre que toute grandeur assignable , si petite que soit celle-ci, sans jamais devenir nulle.

Exemple : Soit la faction  «  » , supposons qu’on attribue au diviseur « n » des valeurs croissant indéfiniment au-delà de toute limite, par exemple , les valeurs « 10 ; 100 ; 1000 ;….»qui se décuplent sans cesse à partir d’une valeur initiale «  n = 10 » .

La fraction «  » prendra les valeurs successives «  » ; elle approchera indéfinitivement et d’aussi près qu’on veut de zéro, sans jamais s’annuler rigoureusement ; cette quantité «  » s’appellera un « infiniment petit ».

2°) Quantité infinie.

On appelle « infinie » ou « infiniment grande » une quantité susceptible de prendre des valeurs absolues successives « indéfiniment croissante » , en sorte que cette quantité finisse par dépasser en valeur absolue tout nombre  donné , si grande qu’il soit . 

L’infini se désigne d’ordinaire *  par le signe : 

* :  Le symbole «  » est employé depuis Wallis ( Arithmética infinitorum  1655) pour signifier l’infini ; ce n’est peut être qu’une déformation de l’initiale  du mot « mille » en écriture romane, mot employé pour désigner un nombre très grand. Chez les Hindous , les algébristes indiquaient l’infini par l’unité divisée par zéro.

Exemple :

Assignons au diviseur « p » de la fraction  «  » des valeurs absolues indéfiniment décroissantes , tel que «  0,1 ; 0 ,01 ; 0,001 ; 0,0001 ;….la fraction prendra des valeurs inversement croissantes ; «  » ; «  » ;  «  » ; «  » ;…  ou «  30 ; 300 ; 3000 ; 30 000 ; … » et tandis que « p » devient « indéfiniment petit » la fraction «  » croît au-delà de toute grandeur donnée. Cette quantité «  » s’appelle un « infiniment grand » et l’on écrit  que «  =    »

En Mathématiques , sous les noms « infiniment grand «  et « infiniment petit » ,on désigne donc pas des quantités  actuellement  déterminées et assignables , l’une extrêmement grande , l’autre extrêmement  petite , mais des « quantités variables », actuellement indéterminées en valeurs , l’une en voie de grandir au-delà de toute grandeur assignable , l’ autre en marche vers zéro, mais sans jamais l’atteindre .

En réalité , il ne peut exister une « quantité » qui , au sens absolu et littéral des mots, soit infiniment grande ou infiniment petite .

Il ne peut exister, croyons nous, ni une collection composée d’un nombre infini d’objets existant simultanément , ni un être ayant commencé, depuis un nombre infini d’années, d’exister.

Tout « nombre » proposé  est essentiellement déterminé et fini. En effet, si grand soit-il, il en existe un plus grand encore , car on peut y ajouter ne fût ce qu’une unité , on peut même le doubler , le tripler , le multiplier par tel nombre qui plaît, on peut même élever au carré , au cube  , à telle puissance qu’on souhaite. Si petit soit –il au contraire , on peut  le diviser par « 2 » , puis chaque moitié par « 2 » , et ainsi de suite .

De même , dans l’espace, une ligne droite donnée a nécessairement une certaine longueur déterminée et finie ; car on peut poursuivre cette droite dans l’une et dans l’autre direction, à l’infini ou plutôt à « l’indéfini », comme on peut, au contraire, par la pensée, partager cette droite en deux moitiés et ces moitié encore , et ainsi de suite sans être jamais arrêté.

De même , dans le temps, la durée  de l’existence d’un être qui a commencé par exister à un moment donné, à une certaine valeur actuelle déterminée ( un certain age) ; par la pensée, on peut prolonger à l’indéfini cette durée, en y ajoutant sans cesse et sans limite ; on peut aussi , au contraire , partager par la pensée la durée d’une vie en deux moitiés , et chaque moitié encore ainsi de suite. ,,

L’infini absolue n’est pas un nombre , ce n’est pas une quantité numérique ; non plus que l’immensité absolue n’est une quantité d’espace , ni l’éternité une quantité de temps .

Inversement « zéro » n’est une quantité infiniment petite , un fragment infinitésimal d’unité ; non plus que l’instant actuel n’est une portion de temps, ni le point une portion de longueur .

3°)  Limite

Quand les valeurs successives  d’une quantité variable « x » approchent indéfiniment d’une quantité fixe et déterminée « a », de manière à n’en différer que d’aussi peu qu’on veut , cette quantité fixe et déterminée est appelée «  la limite » des valeurs de la variable. C’est ce qu’on exprime par l’égalité : «  lim.x = a »

Nous vous citons quelques exemples.

N° 1 :  La fraction «  » , dans l’hypothèse où « n » désigne une quantité variable  indéfiniment croissante , a pour limite zéro , et l’on écrit :  « lim.  = 0»

N° 2 :  Le rapport  «  » , si l’on assigne à « n » les valeurs successives «  1 ; 2 ; 3 ; 4 ; … »et ainsi de suite indéfiniment , devient successivement «   » et la différence « d » entre ce rapport et l’unité , « d = = =  » devient moindre que toute grandeur assignable , si l’on prend « n » suffisamment grand ; on a donc « lim.  = 1 »

N°3 : L’expression , si l’on attribue à « n » les valeurs entières successives indéfiniment croissantes «  0 ; 1 ; 2 ; 3 ; 4 ;5 ;… »devient successivement : «  +1 ;  ;…..»et converge vers zéro en oscillant indéfiniment, mais de plus en plus faiblement, autour de cette valeur limite , qu’elle n’arrive jamais à atteindre : « lim. =0 »

N°4  : La somme «  S_p » des « p » premiers termes de la série :  «  1 +  » approche indéfiniment et d’aussi près de « 2 » ,

 si l’on addition un nombre suffisamment grand de termes. En effet, en additionnant    « 2 ; 3 ; 4 ; 4 ; 5 ; 6 ; 7 . ;…. »termes on obtient successivement les sommes :

«  » ou en général  «  »  , en désignant  par « m » le dénominateur de la dernière fraction additionnée.

Or  «   = 2 -  » , et pour « m » infiniment grand, on a « Lim.  = 2

N°5  : Nous avons déjà vu  ( on appelle « série » une suite illimitée de termes se  déduisant les uns des autres suivant une loi déterminée.)  comment certains quotients se prêtent à un développement en série , et comment , par exemple l’identité :

« = 1 + x + x² + x³ + x⁴+ …. » pour « x =  » , fournit la sommation :    «  2 = Lim (1 +  ) » 

N°6   : Nous avons vu, en arithmétique,   qu’une « fraction périodique » , si l’on prend un nombre indéfiniment grandissant de périodes

 Converge vers la valeur de sa fraction génératrice . Ainsi , « lim . 0,33333…=  ».

En effet :

 - 0,3 =   -  =

 - 0,33 =   -  =

 - 0,333 =   -  =

Et ainsi de suite .

N°7   : On sait aussi  que le nombre « incommensurable » représenté par le symbole  est la limite commune des nombres commensurables , les uns indéfiniment croissants ( 1 ; 1,4 ; 1,41 ; 1, 414 ; …) , les autres indéfiniment décroissants  ( 2 ; 1,5 ; 1,42 ; 1,415 ; ….) dont les carrés ont « 2 » pour limite :

 =  1, 414 213 56 .. »

La définition du mot « incommensurable » , comme limite d’une suite de nombres commensurables, est de Cauchy ; le géomètre belge CATALAN ( 1814-1894) a repris cette notion et a donné le premier , dans ses excellents Manuels d’Arithmétique et Algèbre ( 1852 et 1857) , la véritable théorie des « incommensurables » , devenu aujourd’hui classique.

N°8    : En géométrie , on pose cette définition : la tangente à une courbe en un point donné de la courbe est la limite des positions d’une sécante, qui coupe la courbe en ce point, et qui tourne autour de ce point de façon qu’un second point de section tende à se confondre avec le premier.

N°9    : En géométrie encore ; on établit ces deux définitions : «  on appelle longueur de la circonférence la limite du périmètre »  et « aire du disque la limite de l’aire d’un polygone convexe inscrit dont les côtés  deviennent  indéfiniment plus nombreux et diminuent indéfiniment de manière à devenir moindres que toute grandeur donnée.

4°) Remarques : 

Remarque N°1 : La complète et rigoureuse « définition » de la limite mathématique se formule en ces termes :

On entend par « limite » d’une quantité variable « x » , une quantité fixe « a » dont les valeurs successives de la quantité variable s’approchent indéfiniment , de manière que la différence « x – a » , prise en valeur absolue, entre cette variable et cette quantité fixe , finit par devenir définitivement   plus petite  que toute grandeur assignable , si petite que soit celle-ci, sans que cette différence devienne  jamais définitivement nulle.

DE cette définition résultent les conséquences suivantes :

1°) Il y a équivalence entre les égalités   «  lim. x = a » et «  lim. x – a = 0 »

2°) Une « quantité indéfiniment  petite » peut se définir une « quantité variable » qui a zéro pour limite.

3°) Une « quantité infiniment grande » peut se définir « une quantité variable successible de croître au-delà de toute limite *».

·       info : L’infiniment petit et l’infiniment grand sont les deux modes extrêmes de la quantité, qui, dans ses variation tend vers le néant ou vers l’infini.

·       Zéro est la limite de l’infiniment petit.

·       Dira – t –on que « l’infini » est la limite de « l’infiniment grand » ? Non : cette locution serait vicieuse à tous égards ; on ne pourrait même interpréter en entendant , par cette limite et par cet infini absolu, je ne sais qu’elle barrière idéale placée au-delà de toute quantité. L’infini absolu ne peut jouer le rôle de limite : il n’est que la simple négation de toute limitation , il est une pure conception de notre esprit , et non une grandeur réelle, une quantité.

·       En Mathématiques , le mot « infini » a toujours un sens conventionnel.

·       D’ordinaire, il signifie une quantité susceptible de croître sans limite , un « indéfiniment grand ».

·       Quelque fois , surtout comme solution d’un problème , « l’infini absolu » apparaît : il signifie alors que , dans les conditions données , la quantité cherchée cesse absolument d’exister. On demande à quelle distance « x » de son origine la droite « A » est rencontrée par une droite « B », et le résultat du calcul est « x  =  » ; on conclura : il n’y a pas de point de rencontre , les deux droites sont parallèles.

·       Rappelons que : un nombre « infini » implique contradiction. Tout « nombre » est déterminé et fini.

Remarque N°2 : Entre la variable et sa limite il y a une « différence de nature », qui s’oppose à ce que l’une finisse jamais par se confondre formellement avec l’autre.

Aussi « zéro » n’est aucunement une fraction infiniment petite : il ne peut exister un fragment de l’unité, si petit soit –il , qui soit néant. Un infiniment  petit ne diffère d’une fraction ordinaire que par la dimension , laquelle a cessé d’être perceptible et même concevable , son diviseur excédant tout nombre susceptible d’être formulé.

De même un cercle n’est pas un polygone à côtés excessivement petits : le cercle n’a pas de côtés ; uns courbe n’offre nulle part trois points consécutifs en ligne droite.

Cependant, il peut arriver qu’une variable atteigne une ou plusieurs fois , ou même périodiquement, la valeur particulière de sa limite : elle ne se confond  pas définitivement ni formellement avec sa limite, elle traverse cette valeur ;

Exemple : Soit la fraction « x= , dans laquelle on suppose « n » croissant indéfiniment. ON a  « lim.x = 3 » ; on peut en effet, s’en assurer en écrivant la fraction  sous la forme : «  x =  »  : si « n » est infiniment grand, les termes : «  » deviennent infiniment petits et s’évanouissent.

Cependant, posons successivement «  n = 1 ; n = 2 ; n = 3 ; n = 4 ; n = 5 ;… » ; il vient : «  ;  ;  ;  ; …. » ainsi de suite ; la variable , partant de la valeur « x = 4 » , décroît , passe par la valeur « 3 »et décroît encore , pour revenir ensuite converger vers sa limite « 3 ».

En trigonométrie , le rapport «  » tend vers zéro, quand « x » croît indéfiniment ; mais toutes les fois que « x » devient égal à un multiple de la demi – circonférence ,le rapport s’annule et change de signe : cette variable oscille de part et d’autre de sa valeur limite « zéro », tout en se resserrant de plus en plus auprès d’elle.

La valeur « maximum » et la valeur « minimum » d’une quantité variable ne constituent pas des « limites » au sens mathématique de ce mot.

Ainsi les cordes inscrites dans un cercle ont pour longueur maximum la longueur du diamètre : le diamètre n’est cependant pas la limite des cordes , ce n’est qu’une corde plus grande que les autres ; il n’en diffère point par nature .

De même en trigonométrie, le rayon est le maximum , et non la limite proprement dite, du sinus..

Remarque N°3 : On classe en divers « ordres » les infiniment grands et les infiniment petits.

Soit «  » une quantité infiniment grand : son carré «  » est infiniment grand par rapport à elle ; son cube « n³ » est infiniment grand par rapport à son carré, et ainsi de suite . Ces infiniment grands sont du premier , du second et du troisième ordre.

Inversement , la fraction «  » étant infiniment petit du premier ordre , son carré et son cube sont des infiniment petits du second et du troisième ordre : ces infiniment petits marchent tous vers le néant , mais accélèrent inégalement leurs pas : «  » est déjà évanouissant, quand «  » est encore perceptible , «  »  est déjà lui – même infiniment petit par rapport à «  ».

5° ) Principe fondamental

Deux variables constamment égales entre elles dans tout le cours de leurs variations , tendent vers des limites égales.

Ce principe est évident, à la condition que l’on conçoive nettement la notion exacte de la limite. En effet, si «  » et «  » varient simultanément et restent constamment égales , « » ne peut approcher indéfiniment d’une valeur fixe et déterminée «  » et se tenir dans un voisinage de plus en plus resserré de cette valeur «  » , sans qu’il en soit de même de son égale « y » ;Donc , si « x = y »  , on a «  lim  = lim  » .

Ceci  termine ces premières notions relatives aux limites. (voir les cours suivants  ….)

Refaire les exercices du cours……