|
Le cercle |
|
|
|
|
|
Le cercle et
disque |
|
|
Circonférence |
ENVIRONNEMENT du dossier:
|
Objectif
précédent : |
Objectif
suivant : |
1.
:Aires (présentation) généralités |
DOSSIER :
|
|
1.
Aire du disque , |
|
|
|
|
2.
Aire d’une
couronne |
|
|
|
|
3.
Aire d’un secteur
circulaire |
|
|
|
TEST |
COURS |
Interdisciplinarité : |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
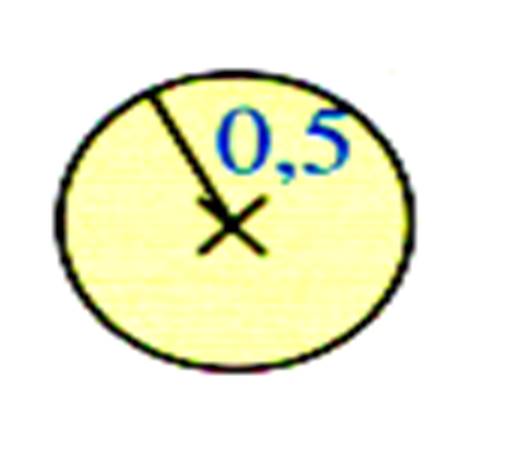
Par définition : Un disque est constitué par l’ensemble des points
de la circonférence du cercle et de sa région intérieur. |
|
|
|
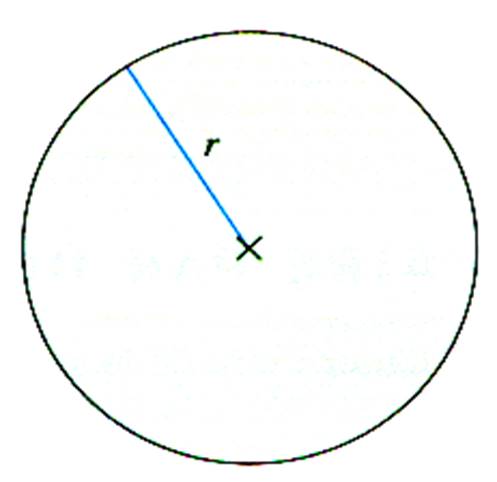
AIRE du disque : |
|
|
|
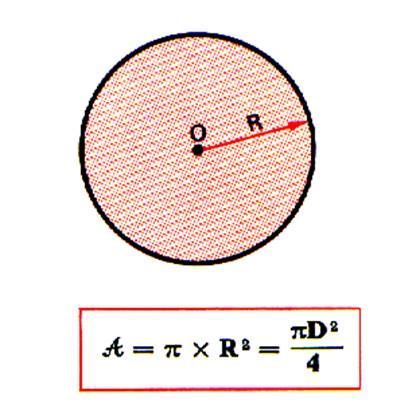
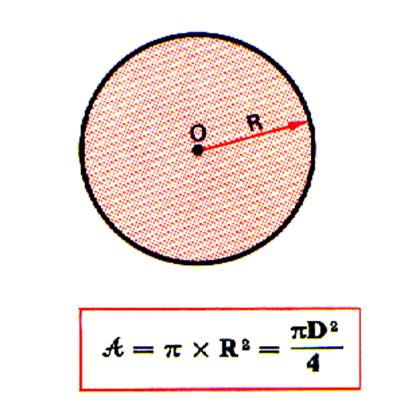
Le disque est la surface colorée. Cette surface est appelée « aire » ;
noté : Ad |
|
|
|
|
|
|
|
|
|
|
|
La mesure de cette surface se ferait après
quadrillage (en mm , ou cm ,ou ...) il suffit de
compter le nombre de « carrés » ; on obtient, aussi ,la valeur de cette Aire en utilisant la
relation : p = Formule à retenir pour les cas courants: L’Aire du disque est
égale au produit de « pi » par le « carré du rayon ». ( on prendra : pi = 3,14 ) |
|
|
|
|
|
|
|
Modèle
mathématique : Ad = 3,14 R2 On peut aussi
dire : L’aire
du disque est égale au produit de la longueur de la circonférence par le
rayon divisé par « 2 » A = 2p r |
|
|
|
|
|
|
|
Application : Exemple : Trouver l’aire d’un disque de 3m de rayon. Réponse : A = 32 |
|
|
|
Aire de la couronne : (Info plus ++++) |
|
|
|
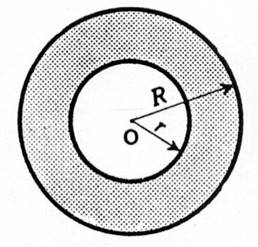
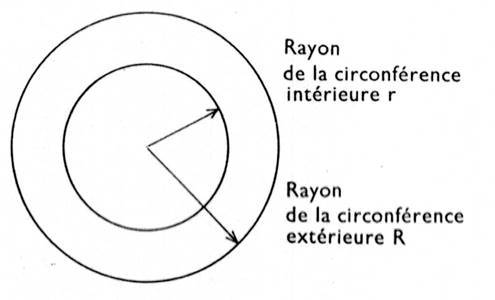
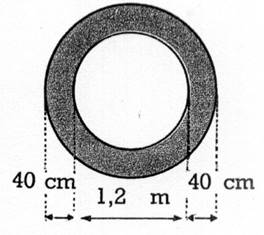
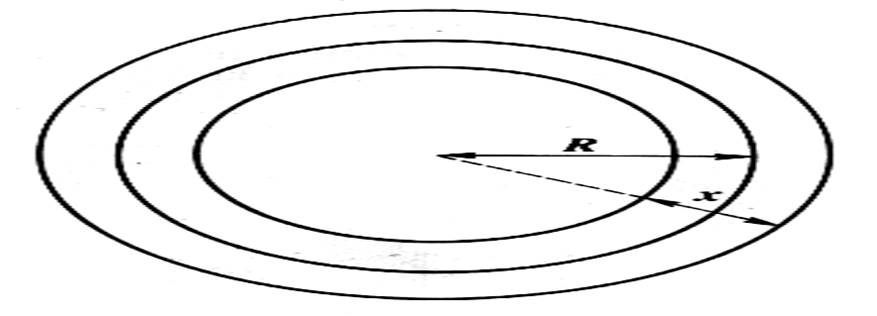
On appelle « couronne circulaire » la
surface comprise entre deux circonférences concentriques. On obtient l’aire de la couronne en retranchant
l’aire du petit disque à celle du grand disque. A = p R2 - p r2 ( on factorise
par « pi » ) Ce qui revient à multiplier par « pi »
la différence des carrés des rayons. A = p ( R2 - r2 )
|
|
|
|
|
|
|
|
Application : Trouver l’aire de la couronne , sachant que les rayons des cercles ont Solution
1 : Aire du grand disque = 82 Aire du petit
disque = 62 Aire de la couronne = 201,0624 cm2 -
113,0976 cm2 = 87,9648
cm2 Nota : en appliquant le deuxième formule ,
on arrive plus facilement au résultat : A = p ( R2 - r2 ) A = p ( 82
- 62 ) =p (
64 - 36 ) =28 1 ) Calculer l ‘ aire du disque de Corrigé : a
)inventaire de ce que je connais : Ad = 3,14 R2 et R =10 cm b) On remplace dans Ad la valeur de R : Ad = 3,14 c) Calcul :
3,14 d) Conclusion : l ‘ aire du disque est de 314 cm2 2 )Calculer l ‘
aire du disque de 10cm de diamètre. Corrigé : a )inventaire de ce que je connais : Ad =
3,14 R2 et D =10
et D = 2 R à ce niveau deux
sont possibles : je cherche
la valeur du rayon et j’applique cette valeur dans la « formule »
ou je garde la valeur du diamètre j’applique la « formule » Ad = 3,14 ( D2 / 4) .Les deux démarches conduisent au même
résultat. b) Je calcule R : R
= 10 :2 ; R= c) On remplace dans Ad = 3,14 R2 ;
Ad
= 3,14 52 d) Calcul :
3,14 e) Conclusion : l ‘ aire du disque est de 78,5 cm2 |
|
|
|
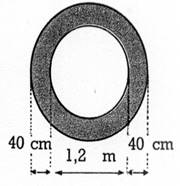
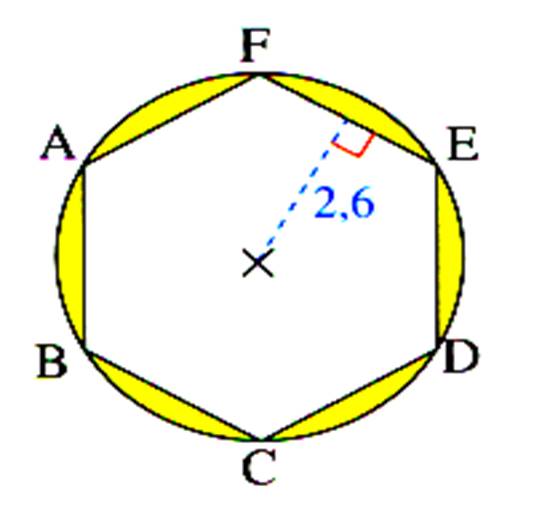
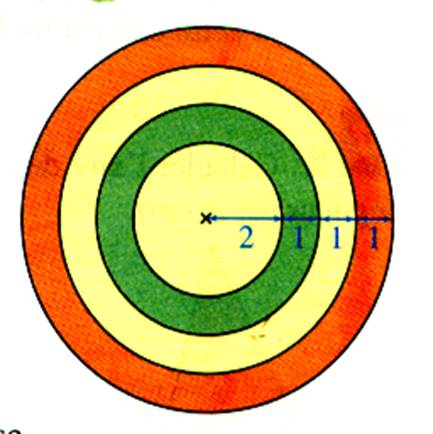
Activité : Calculer l’aire de la couronne ci-contre.
|
|
|
|
|
|
|
|
AIRE D’UN
SECTEUR CIRCULAIRE . |
|
|
|
On obtient l’aire d’un secteur circulaire en multipliant l’aire du disque par le nombre de degrés de l’arc et en
divisant le produit par 360 |
|
|
|
|
|
|
|
Le secteur circulaire : |
|
|
|
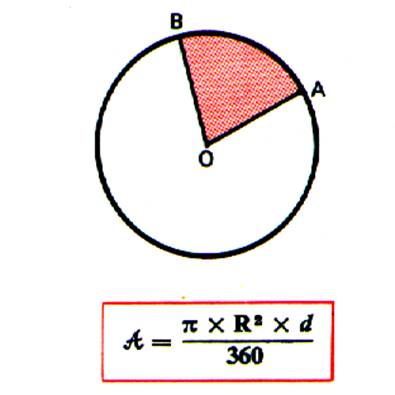
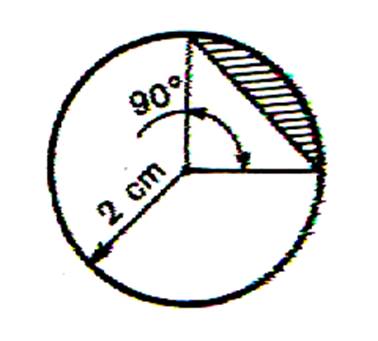
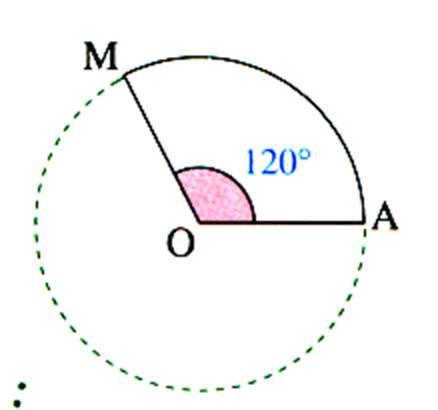
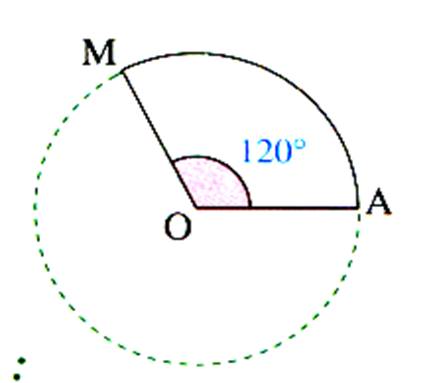
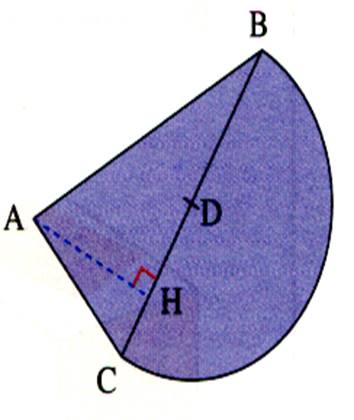
On appelle « secteur circulaire » l’aire comprise entre un
arc et les deux rayons ( OB et OA ) qui aboutissent à ses extrémités.
Aire :
on obtient l’aire d’un secteur circulaire en multipliant l’aire du disque par
le nombre de degrés de l’angle du secteur et en divisant par 360. |
|
|
|
A = p r2 |
|
|
|
|
|
|
|
Info sur : SOS ARC
et angle
|
|
|
|
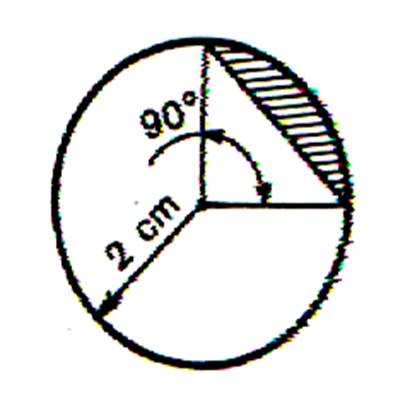
Application
Trouver l’aire d’un secteur circulaire dont le rayon du cercle a 1° aire du disque = 52 2° aire du secteur : 78,54
|
|
|
|
|
|
|
|
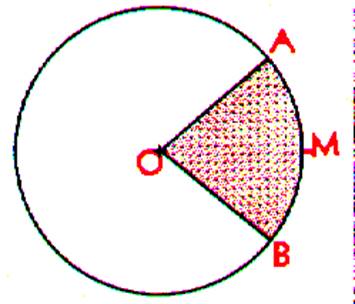
Segment circulaire : Info
plus ++++ |
|
|
|
On
appelle segment circulaire
l’espace compris entre un arc et la corde qui la sous tend |
|
|
|
Le secteur circulaire
peut être ( très souvent le cas ) exprimé en
degré ; ou en grade : (info ++) |
|
|
|
Calcul de
l’aire d’un secteur circulaire
dont l’angle est exprimé en degrés : |
|
|
|
Formule : A = |
|
|
|
On divise l’aire du disque en 360 parties égales ; pour
multiplier par le nombre degrés ( |
|
|
|
|
|
|
|
Exemple : Si l’angle
alpha( On sait que A = soit :
A = l’aire
du secteur circulaire est de 641 mm2 |
|
|
|
|
|
|
|
En statistique une des
représentations graphiques des pourcentages est le « diagramme
circulaire » .
La circonférence est divisée en 100 parties égales ; Relation entre % et
valeur en degré : 360° représente 100% ;
soit Relation entre % et
valeur en grade : 400 gr.
représente 100% ; soit Le 1% représente 4 grades d’angle . |
|
|
|
|
|
|
|
Travaux auto – formatifs. |
|
|||||||||||||||||||||||||||||
|
|
1 ) A quoi
est égale l’ aire du disque ? 2 )
Donner la formule permettant de calculer l’aire d’un disque (compléter avec
un dessin coté ) |
|
|||||||||||||||||||||||||||||
|
|
EVALUATION
|
|
|||||||||||||||||||||||||||||
|
|
1°) Donner les formules ; remplacer
les lettres par les valeurs données , faire les calculs . Compléter le tableau
suivant :
|
|
|
|
|
|||
|
|
|
|
||
|
|
La couronne . ( INFO plus en algèbre )
Autres
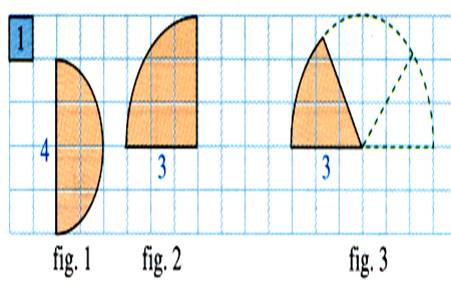
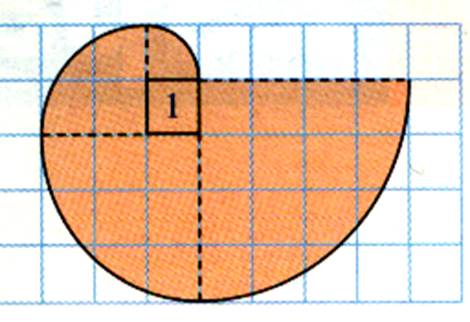
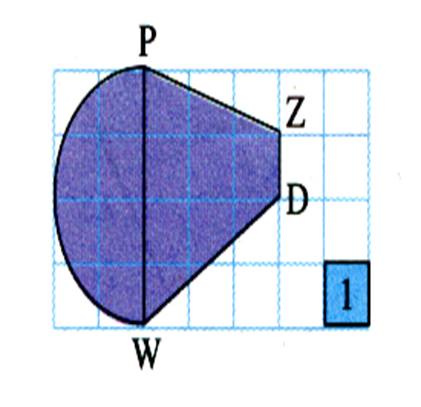
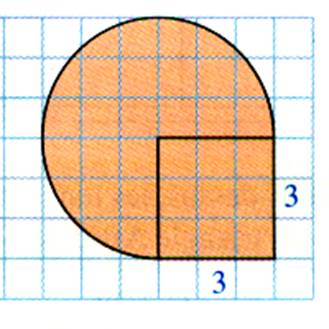
travaux : CALCULER LES AIRES
SUIVANTES. ( avec l’aide des carreaux) |
|
||
|
|
|
|
||
|
|
figure 1 = Figure 2 = Figure 3 = |
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
II )
DETERMINATION DE L’AIRE par CALCULS :
|
|
||
|
|
|
|
|
Dessins a
exploiter |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
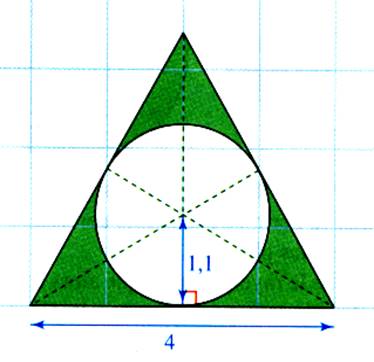
Calculer l’aire du triangle , l’aire du disque
inscrit , l’aire de la surface colorée. |
|
|
Un carré mesure
|
Calculer l’aire du carré , l’aire du disque
inscrit , l’aire de la surface colorée. |
|
Evaluer l’aire en carré . |
|
Série 3 :
1°) quelle est l’aire en mm² , puis en cm² ,d’un CD
de
2°) Quelle l’aire d’une piste de cirque de
3°) Un bassin circulaire a une aire de
Série 4 :
4°) Quelle est en mm la mesure du diamètre d’un
disque dont l’aire est égale à 19 ,625 cm² ?
5°) Quelle est l’aire en m² du rond central d’un
terrain de football sachant que le
diamètre mesure 18,3 m ? ( arrondir au m² par excès )
6°) Quelle est l’aire de verre nécessaire à la
réalisation d’une table circulaire de