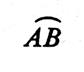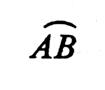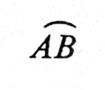Pré requis:

Le cercle
« Arcs » et « angles »

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent : Le cercle (vu en 6^ème collège)

Objectif suivant : · Les angles inscrits · Le cercle (calculs)

tableau Info sur les cours en géométrie. Liste des cours sur les angles

DOSSIER : ARCS et CORDES et flèches

1. Définitions :« ARC » de circonférence 

2. Arc de cercle : (et angle au centre)

3. Définition : « Corde » 

4. Flèche d’un arc  :

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité Fiches d’activités	Corrigé Contrôle	Corrigé évaluation

COURS

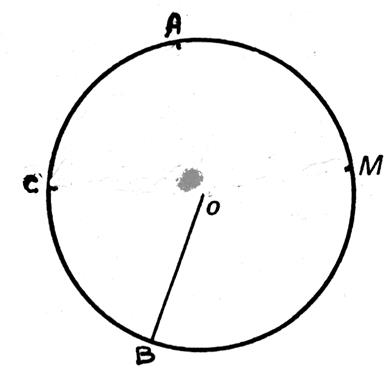
« ARC » de circonférence : Définition : un arc de circonférence est une portion de circonférence limitée par deux points.
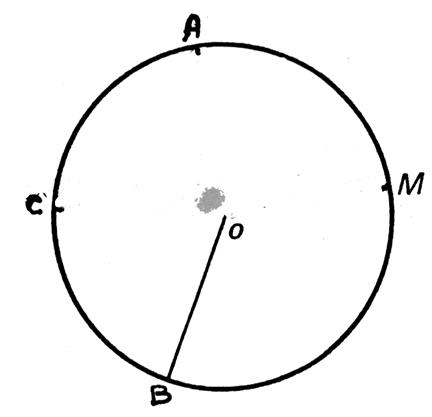
Les deux points « A » et « B » limite sur la circonférence deux arcs  « AMB » et « ACB » : Que l’on note : Sauf indication contraire , la notation désigne le plus petit arc « AB ». D’après le dessin l’arc AB et l’arc BCA sont identiques.

Arc de cercle : (et angle au centre)	Calcul de la longueur d’un arc : SOS COURS
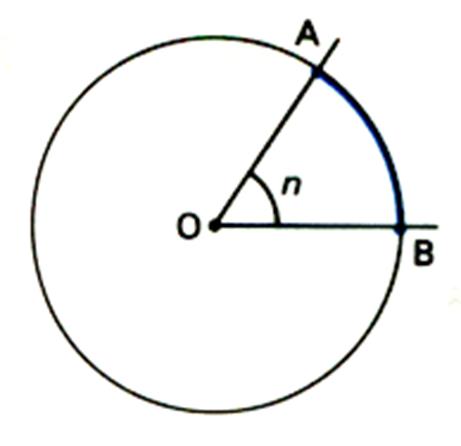
AB est l’arc de cercle limité par l’angle au centre ( « n ») . Notation : Les arcs et les angles sont des grandeurs mesurables : Un arc de cercle et l’angle au centre correspondant sont mesurés par le même nombre , à condition d’adopter pour unité d’angle l’angle au centre qui intercepte l’unité d’arc. Les deux demi-droites OA et OB déterminent deux angles au centre , l’un saillant , l’autre rentrant.
L’unité d’arc est le quadrant (le quart de cercle) ; l’unité d’angle correspondante est l’angle droit .(1 droit )
Pour en savoir plus ++++

Définition : « Corde » : une corde est un segment de droite joignant deux points d’une circonférence.
On dit que la corde AB sous tend l’arc qui a les mêmes extrémités.

CORDE :
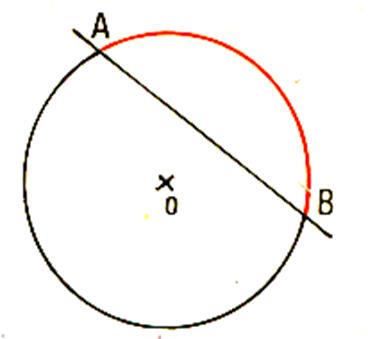
Le diamètre passant par OH est un axe de symétrie . Par pliage autour de l’axe « x » les points A et B se superposent . La droite D intercepte le cercle en A et B . La partie de cercle compris entre les deux points A et B s’appelle « arc ». Le segment A B est perpendiculaire au diamètre , et est appelé « corde »

INFO plus +++++ rechercher le centre d’un cercle ou disque

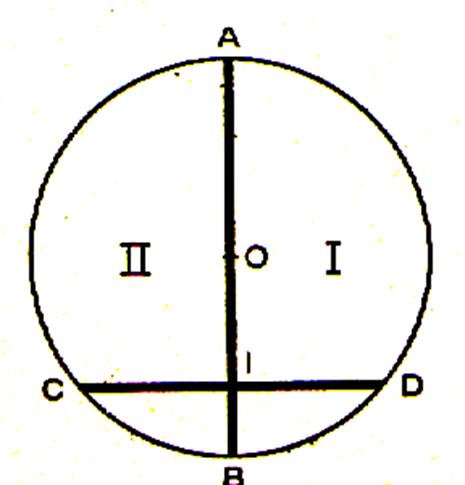
Le diamètre perpendiculaire à une corde partage cette corde et les deux arcs qu’elle sous-tend en deux parties égales . Le pliage autour de AB fait coïncider le demi-cercle ( I ) avec le demi – cercle ( II) La demi droite ID perpendiculaire à AB se superpose à la demi-droite IC et le point D devant se trouver à la fois sur IC et sur le demi-cercle (II) coïncide avec C. On conclut que : IC = ID ; l’arc AC = l’arc AD ; l’arc BC = l’arc BD

Flèche d’un arc  :
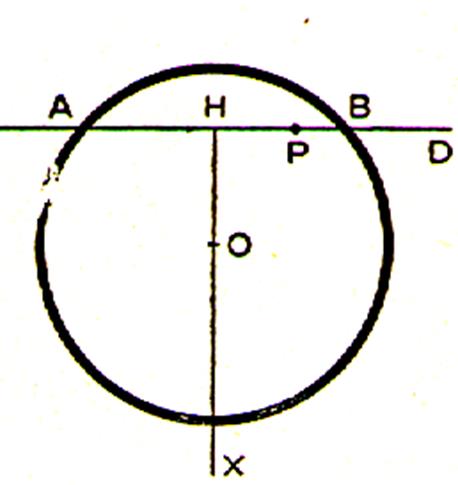
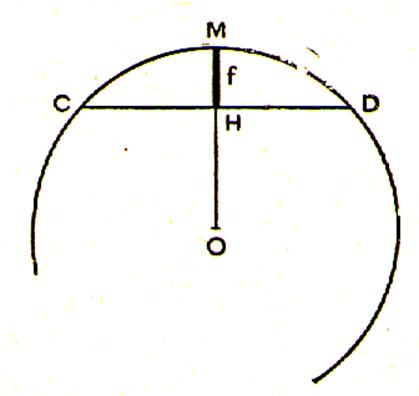
On appelle flèche d’un arc le segment de droite qui joint le milieu de cette arc au milieu de la corde qui le sous-tend. La droite qui porte la flèche est médiatrice de la corde et passe par le centre du cercle . MH représente la flèche de l’arc CD .

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°) Donner la définition d’ un arc et d’une corde.

2°)

Nommer les arcs.

EVALUATION:

1°) Tracer un cercle ; placer deux points formant un arc et deux autres limitant la corde.

2°) Tracer toutes les cordes .