Angle  e ARCS

Cercle

Index      accueil warmaths

Objectif précédent :

1.     1°)L’angle et sa mesure

Objectif suivant :

1.     Mesure d’un arc au rapporteur .

2.     conversions

Info gêné :

Liste des cours en géométrie.

Liste des cours sur les angles.

DOSSIER :    NOTIONS d’arc et arcs interceptés (et angle : son extension)

1°)« arc de cercle »

2°),Comparaison de deux arcs d’un même cercle .

3°) ARC et ANGLE 

4°) ANGLE au CENTRE .

5°) ANGLES au CENTRE et   ARCS INTERCEPTES .

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle 

Corrigé évaluation 

COURS

1°)« arc de cercle »

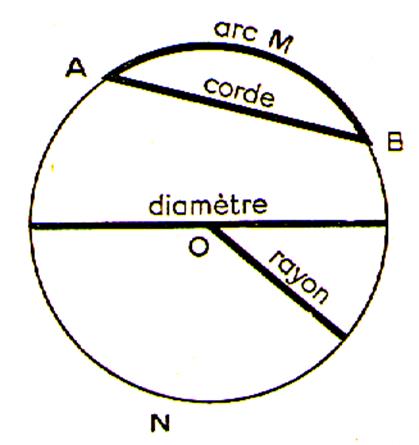
Définition : On appelle « arc de cercle » la portion de cercle comprise entre deux points de ce cercle .

AB est la portion de cercle appelé « arc » :

          On désigne l’arc de cercle représenté par « arc AMB » , on écrit en abrégé    ;    Remarquer l’arc

2°) Comparaison de deux arcs d’un même cercle .

Proposons – nous de comparer deux arcs AMB et CND qui appartiennent à un même cercle . A l’aide d’un papier transparent , nous calquons  l’arc CND , puis plaçons ce calque de façon que les extrémités A et C soient superposées et que les deux arcs aient une partie commune .

Trois cas peuvent se présenter :

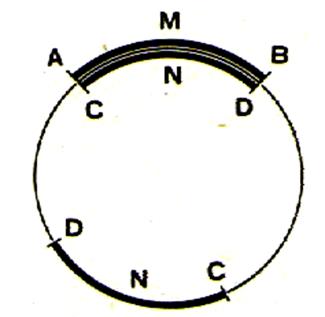
1°) Les extrémités B et D sont confondues :

Les deux arcs coïncident ; nous disons qu’ils sont égaux

Nous écrivons   =

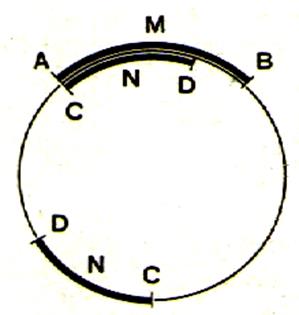
2°) l’ extrémité D se place entre  A et B

L’arc CND est plus petit que l’arc AMB .

nous écrirons : <

ou bien  l’arc AMB est plus grand que l’arc CND :

nous écrirons :  >

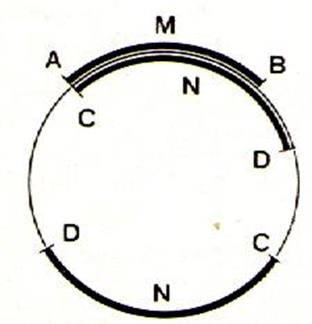
3°) l’ extrémité D se place au-delà de B

        L’arc CND est plus grand  que l’arc AMB .

nous écrirons :  >

ou bien  l’arc AMB est plus petit que l’arc CND :

nous écrirons :  <

3°) ARC et ANGLE  .

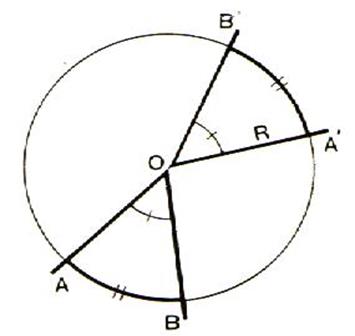
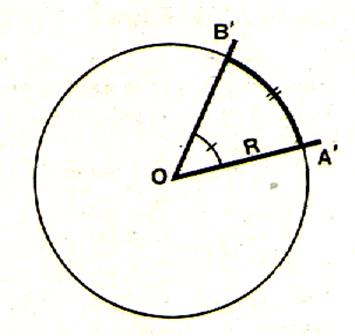
Important :

Si deux angles au centre AOB et A’OB’ pris sur un même cercle ou sur deux cercles de même rayon  sont égaux  , ils interceptent des arcs égaux ;(voir figure)

Pour cette raison , les unités de mesure  des angles sont définies à partir des unités de mesure des arcs .

4°) ANGLE au CENTRE .

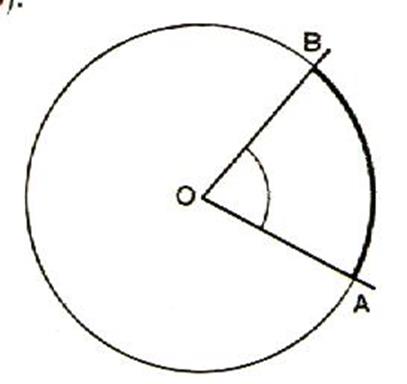
Définition :

Un angle au centre est un angle qui a son  sommet au centre d’un cercle .

La portion de cercle comprise entre les côtés d’un angle au centre est l’arc intercepté par cet angle .

Dans la figure ci – contre   l’angle au centre AOB intercepte l’arc AB

5°) ANGLES au CENTRE et   ARCS INTERCEPTES .

Sur un cercle quelconque , considérons un arc AB qui mesure par exemple ;25 degrés – arcs ; Cet arc est la somme de 25 arcs de 1degré – arc chacun .

A chacun de ces arcs de 1 degré – arc correspond un angle au centre de 1 degré -  angle .

L’angle au centre AOB est la somme  de 25 angles de 1 degré – angle  chacun , donc il mesure 25 degrés – angles .

Ainsi on utilise des unités  concordantes pour les arcs et pour les angles , un angle au centre  et l’arc qui l’intercepte sont mesurés par le même nombre .

Chapitre suivant :    les conversions

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Donner la définition de « arc de cercle » :

EVALUATION:

Sur un cercle , marquez trois points distincts A , B , C  . Nommer  tous les arcs formés . Pour désigner certains de ces arcs , vous pouvez être amenés  , afin d’éviter les confusions , à placer une lettre supplémentaire entre les deux lettres  qui désignent les extrémités de l’arc.