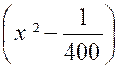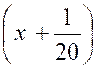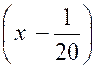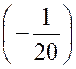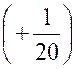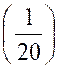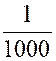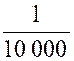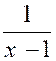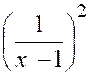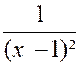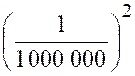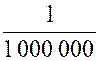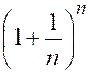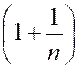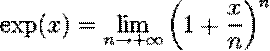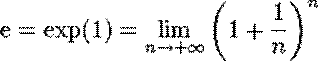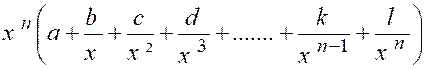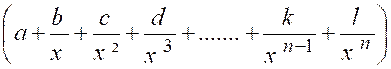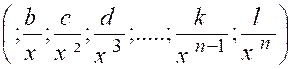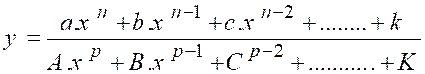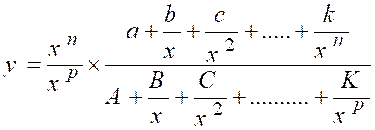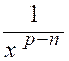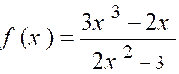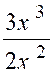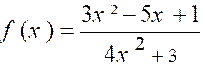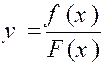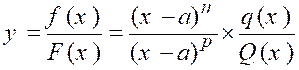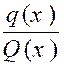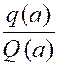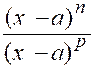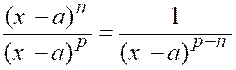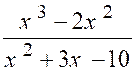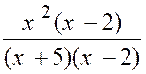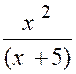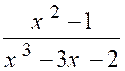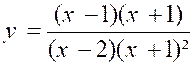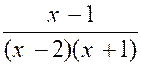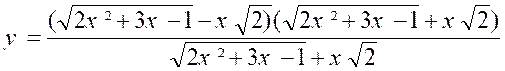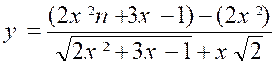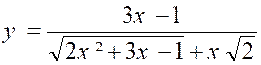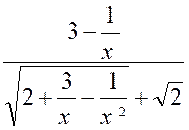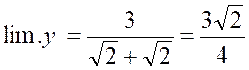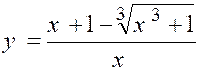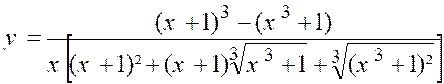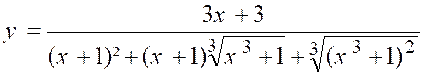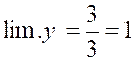Chapitres

1.      Définitions

2.    limites d’une somme de fonction : d’un produit ; d’un quotient ; d’une puissance ;d’une racine ; ( Théorèmes)

3.     Valeurs remarquables d’une fraction.

4.   Valeur d’un polynôme en « x », pour « x » infini.

5.   Valeur d’une fraction rationnelle pour « x » infini.

6.   Limite d’une fraction rationnelle dont les deux termes tendent simultanément vers « zéro »

7.   Calcul de quelques limites.

Cours en lien avec les études de fonctions………….

1°)  Définitions

Soit « y » une quantité variable, fonction d’une autre quantité variable attribuée à « x ».On dit que « y » a pour limite « b » quand « x » tend vers « a » ,si, lorsqu’on donne à « x » des valeurs suffisamment voisines de la valeur « a » , les valeurs correspondantes de « y »  différent d’aussi peu qu’on le veut de la valeur de « b ».

La quantité « y » tend vers la limite « b » par valeurs supérieures ou par valeurs inférieures , suivant que la différence «  y – b » reste positive ou négative.(voir la suite pour les deux exemples)

On dit qu’une quantité « devient infinie » si elle parvient à dépasser en valeur absolue tout nombre arithmétique si grand qu’on puisse le concevoir.

Une quantité algébrique peut devenir infini de deux façons :

Soit en étant positive, soit en étant négative.

Dans le premier cas, on dit quelle « croît indéfiniment »  par valeurs positives, ou encore qu’elle tend vers « +  » ;

Dans le second cas ,  on dit quelle « décroît indéfiniment »  par valeurs négatives, ou encore qu’elle tend vers « -  »

Remarque : Lorsqu’une quantité devient infinie par valeurs positives ou négatives , on dit souvent qu’elle croît « indéfiniment ».

Attention : Cette façon de parler , consacrée par l’usage, est évidemment incorrecte lorsque la quantité est  négative , puisqu’alors elle décroît quand elle tend vers « -  » .

L’expression « croître indéfiniment » se rapporte donc, en somme, à la valeur absolue de la quantité qui devient infinie.

Exemples :

Exemple N°1 : La fonction  «  y =  4 x² + 3 » a pour  limite  « 3 » quand on fait tendre « x » vers « 0 »

Remarquons d’abord que la différence  « y – 3 = 4 x² » étant toujours positive quand « y » tendra vers sa limite « 3 » par valeurs supérieures ?.

Il faut prouver qu’on peut prendre « x » assez voisin de « 0 » pour que la différence «  y – 3 » soit aussi petite que l’on veut , par exemple : <

Or, il suffit, pour cela, que « x » vérifie l’inégalité «  4 x² <  »

Info +++

Ou :        4  =  4   <  0

On donnera  à « x » une valeur comprise entre   et   ; c'est-à-dire inférieure à   en valeur absolue.

On pourrait de même rendre «  y – 3 » plus petit que   ;  , etc.…..donc « y » tend vers « 3 » par valeurs supérieures , quand « x » tend vers « 0 »

Exemple N°1 : La fonction  «  y =  »  devient infinie quand « x » tend vers « 1 ». IL faut montrer que , pour des valeurs de « x » assez voisines de « 1 » , « y » peut dépasser en valeur tout nombre arithmétique si grand qu’il soit, par exemple «  1 000 000 »

Quelque soit le signe de « y », son carré devra être supérieur à  ( 1 000 000)² :

D’où l’on déduit   >    ( 1 000 000)²    ;     soit     >    ( 1 000 000)²

D’où l’on déduit :   ( x – 1 ) ²  -  <  0

Et par suite :   « 1 -   <  x   <  1 +   »

Il suffit donc que la valeur de « x » choisie diffère de « 1 » , en plus ou en moins de moins de  «  »

Si « x » est «  > 1 » , « y » est positif ; donc ,  « x » tendant vers « 1 » par valeurs supérieures, « y » croît indéfiniment par valeurs positives.

Si « x » est «  <  1 » , « y » est négatif ; par suite  ,  « x » tendant vers « 1 » par valeurs inférieures, « y » décroît indéfiniment par valeurs négatives .

2°)  Limites d’une somme de fonction : d’un produit ; d’un quotient ; d’une puissance ;d’une racine ; ( Théorèmes)

Théorème 1 : La limite d’une somme algébrique de fonction est égale à la somme algébrique de leurs limites.

Soient , par exemple, « u » , « v » , « w » trois fonctions d’une même variable indépendante « x ».

Si , lorsque « x » tend vers « a » , les fonctions  « u » , « v » , « w » ont respectivement pour limites « A » , « B » , « C », la somme algébrique  « u + v - w »aura pour limite « A +  B - C » .

En effet , soit  «  » un nombre positif donné d’avance aussi petit qu’on veut. Nous allons montrer qu’on peut choisir « x » assez voisin de « a », pour que « u + v - w » diffère de « A +  B - C » de moins de  «  ».

Donnons à « x » une valeur «  a + h », très voisine de « a »  ( « h » étant positif ou négatif, mais très petit en valeur absolue) . Les fonctions  « u » , « v » , « w » ont ayant pour limites « A » , « B » , « C » , prendront pour « x = a + h » des valeurs : « A +  » , « B + » , « C + » ,  très voisines de « A » , « B » , « C » ,

«  » , « » , « » sont des quantités positives ou négatives, suivant les cas, mais qui pourront être réduites autant qu’on voudra.

On a alors pour « x = a + h » :   « u + v - w =  A +  B – C  + ( +  - )  »                        ( 1 )

Or , rien ne limite la petitesse des valeurs absolues des nombres  «  » , « » , « » . On pourra toujours prendre « h » assez petit pour que chacune  de ces valeurs absolues soit inférieures   à «  » ,  «  » étant donné d’avance.

Alors la valeur absolue ( +  - ) sera inférieure à ( +  + ) c'est-à-dire à     «  ».

Il est clair , en effet , que ( +  - ) est , en valeur absolue , au plus égal à la somme des valeurs absolues de  «  » , « » , « ». ( l’égalité a lieu si  «  » et  « » sont de même signe et  «   »  et « » de signes contraires).

Par suite , d’après la relation  ( 1 )  , « u + v - w » différera  de  « A +  B – C » de moins de «  ».

Théorème 2 : La limite d’un produit de fonctions est égale au produit de leurs limites.

Soient d’abord deux fonctions «  u » et  « v » d’une même variable indépendante « x ». 

Si , lorsque « x » tend vers « a », les fonctions «  u » et  « v »ont   respectivement pour limite « A » et « B » , le produit «  u . v » aura pour limite «  A .B »

Soit , en effet ,  «  » un nombre positif donné d’avance aussi petit qu’on veut , il s’agit de prouver que l’on peut prendre « x » assez voisin de « a » pour que «  u . v » diffère de « A.B » de moins de «  ».

Donnons à « x » une valeur «  a + h » , « h » étant positif ou négatif , mais très petit en valeur absolue. Les fonctions « u » et « v » prennent alors les valeurs «A+  » et « B +» très voisines de leurs limites « A » et « B ».

On a ainsi , pour « x  = a + h »

« u . v  =  ( A+ ) (  B +)  = A.B + ( B +  A + .) »   ( 1)

Pour une valeur de « h » suffisamment petite , «  »  et «  » seront aussi petits que l’on voudra. Comme « 3B » et « A » sont des nombres fixes, on peut choisir « h » de manière que «  » soit , en valeur absolue, inférieur à «  », «  » inférieur à «  ».

Alors la valeur absolue  de « B +  A + . » sera inférieure  à  ( +  + ) c'est-à-dire à     «  ».

; et d’ après la relation ( 1) , «  u . v » diffèrera  de « A.B » de moins de «  ».

Soient maintenant trois fonctions « u » , « v » , « w » ayant  respectivement pour limites « A » , « B » , « C », le produit « u v w » peut être considéré comme le produit des deux facteurs : « u.v » et « w ».

D’après ce qui précède, «  u.v » a pour limite « A.B »et « w » a pour limite « C », donc «  u.v.w »a pour limite « ABC ».
Le théorème étant établi pour un produit  de trois facteurs , on l’étendrait de même , de proche en proche , à un produit de « 4 ; 5 ; ….n »   facteurs.

Théorème 3  : La limite d’un quotient de fonctions est égale au quotient de leurs limites.

Soient d’abord deux fonctions «  u » et  « v » d’une même variable indépendante « x ».   qui lorsque « x » tend vers « a » ont respectivement pour  « A » et « B » ; « B » n’étant pas nul.

Le quotient  «  » aura pour limite le rapport «  ».

En effet , posons «  = w » et désignons par « C » la limite de « w » .

Nous aurons alors «  u = v w »

Et comme la limite d’un produit « vw » est le produit des limites « BC » de ses facteurs , on a «  A = BC » et par suite  « C =  ».

Remarque . L’exposé de ce théorème n’est pas rigoureux .Il faudrait d’abord démontrer l’existence de la limite « C » de « w » par un raisonnement analogue à celui du théorème 2.

Mais une telle rigueur n’est pas indispensable dans ce cours  aussi élémentaire. 

La même remarque s’applique au théorème 5 , ci-dessous.

Théorème 4  : La limite de la puissance «  n^ième » d’une fonction est égale à la puissance  «  n^ième » de sa limite.

C’est une conséquence du théorème 2 . Si la fonction « u » a pour limite « A » , «  u ⁿ » , qui est un produit de « n » facteurs égaux à « u » , a pour limite « A ⁿ »

Théorème 5  : La limite de la racine «  n^ième » d’une fonction est égale à la racine «  n^ième » de sa limite.

Soit à chercher la limite de « »  . Posons « «= v »    et appelons « B » la limite de « v ».

 Nous aurons en élevant à la puissance « n » :  « u = v ⁿ »

Mais comme la limite d’une puissance « v ⁿ » est la puissance «  n^ième » de la limite de « v » .   «  A = B ⁿ » d’où l’on conclut :  B =  ce qui démontre le théorème.

Remarque sur l’application des théorèmes précédents.

Les théorèmes sur la limite d’une somme ou celle d’un produit ne sont vrais , en général, que si le nombre des termes de la somme  ou des facteurs du produit est « limité ».

Il faut se garder de les appliquer à des sommes algébriques d’une infinité de termes «( séries) ou à des produits d’un nombre infini de facteurs. 

Exemple . (prépare à l’étude de la fonction exponentielle)

Le produit  quand le nombre « n » des facteurs augmente indéfiniment , n’a pas pour limite « 1 », qui serait le produit des limites , puisque chaque facteur «  »  tend vers « 1 ». On démontre que la limite de  est le nombre «  e = 2,71828 »

Info : Fonction exponentielle réelle

Définitions

Il existe plusieurs points d'entrée possible pour la définition de la fonction exponentielle : par la propriété de sa dérivée (dérivée égale à la fonction), par ses propriétés algébriques (transforme une somme en produit), ou par son développement en série.

Par une équation différentielle

Définition —  On appelle fonction exponentielle l'unique fonction dérivable vérifiant l'équation différentielle et la condition initiale suivante :

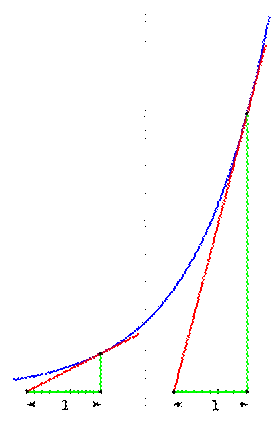
Courbe d'équation « y=exp. (« x ») » et quelques sous-tangentes

Si on note « exp. » cette fonction, le processus de construction conduit à définir « exp.( x ) » par

Le nombre « e »  égal à exp.  (1) est alors défini par

Cette propriété d'être sa propre dérivée se traduit par une propriété sur la sous-tangente à la courbe représentative de exp. La sous-tangente, c'est-à-dire la distance qui sépare le réel x de l'abscisse du point d'intersection de la tangente à la courbe au point d'abscisse x avec l'axe des x est constante et vaut 1.

Info +++

3°)  Valeurs remarquables d’une fraction .  ( info +++ : Cours N°2 sur « les limites »)

Nous ne ferons qu’énoncer les propriétés suivantes, qui sont des conséquences immédiates des théorèmes précédents.

1°) Si un des facteurs d’un produit croît indéfiniment, et  aucun autre ne tendant vers « 0 », le produit va croître  indéfiniment.

2°) Si le numérateur d’une fraction ayant une limite différente de « 0 », le dénominateur tend vers « 0 », la fraction croît indéfiniment.

3°) Si le numérateur d’une fraction restant fini, le dénominateur croît indéfiniment, la fraction tend vers « 0 ».

En résumé, les formes suivantes que l’on rencontre souvent en cherchant la limite d’un produit ou d’une fraction : sont :

«  A x 0 » ;  «  A  x  » ; «  » ; «  »    ; «  »

« A » étant une quantité finie et non nulle, ont des valeurs bien déterminées qui sont : 

«  A x 0 = 0   » ;  «  A  x  =    » ; « =  0  » ; «   =  »    ; «  =  0  »

Si l’un des facteurs d’un produit croît indéfiniment tandis que l’autre tend vers « 0 », ou si les deux termes d’une fraction tendent simultanément vers « 0 », on ne peut rien affirmer.

Le produit ou la fraction peuvent , suivant les cas, tendre vers « 0 », avoir une limite finie « A », ou croître indéfiniment.

Il en est de même d’une fraction dont les deux termes croissent indéfiniment, ou d’une différence dont les deux paries croissent indéfiniment avec le même signe.

Ainsi les formes :

«  x 0 = ?    » ; « = ?  » ;  «    -  =  ?   » ;  «  = ?   » ;       le  « ? » signifie : indéterminé………

(voir plus loin comment on va lever « l’indétermination » ; on dit aussi : comment on calcule la vraie valeur de ces expressions…….. .

4°) Valeur d’un polynôme en « x », pour une valeur de « x » infinie.

Un polynôme entier en « x » , de degré quelconque , croît indéfiniment avec « x » et , pour des valeurs de « x » suffisamment grandes en valeur absolue, il prend le signe de son terme de degré le plus élevé.

Soit , en effet , le polynôme de degré « n ».

«  y = a x ⁿ + b x ^n-1 + c x ^n-2  + ….+ k x + l »

Quand «  x » croît indéfiniment, les différents termes du polynôme, sauf le dernier , croissent indéfiniment , mais sans avoir nécessairement le même signe ; on peut affirmer que « y » augmente indéfiniment.

Exemple : prenons le polynôme :  « 5 x² - 3 x + 2 »  

Quand « x » tend vers l’infini  positif , le polynôme se présente sous la forme indéterminée :  «     -  + 2 »  

Mettons «  x ⁿ » en facteur , nous aurons identiquement :

« y =   »

« y » est maintenant un produit de deux facteurs , dont le premier « x ⁿ » croît indéfiniment avec « x ».

Dans le second facteur   ;    dont les dénominateurs augmentent indéfiniment tendent tous vers « 0 ». (vois chapitre ci-dessus) . La quantité entre parenthèse a donc une limite qui est la somme des limites, c'est-à-dire « a ».

Donc « y » , produit de deux facteurs dont le premier croît indéfiniment et dont le second a pour limite « a » ( quantité non nulle) croît indéfiniment.

De plus, comme la parenthèse a pour limite « a » , on peut prendre « x » assez grand en valeur absolue pour que cette parenthèse diffère d’aussi peu qu’on veut de sa limite.

Pour ces valeurs de « x » , elle prend le signe  de « a » et « y » prend le signe de son terme de plus haut degré « a x ⁿ » . Nous retrouvons ainsi le résultat (à revoir dans : « le signe d’un polynôme de degré quelconque »

Notation.

Lorsqu ’ on représente le polynôme par la notation abrégée :  «  f ( x ) » on désigne par   «  f ( +  ) »  et  «  f ( -   ) » ce que devient le polynôme quand « x » croît indéfiniment par valeurs positives  (  x =  ( +  )  )   ou par valeurs négatives ( x =  -  ) .

Exemples

N°1 : quand « x » croît indéfiniment , le polynôme :  «  f ( x ) =  x ⁴ – 3 x  »  croît indéfiniment par valeurs positives , car son terme de plus haut degré  « x ⁴ » est positif, quel que soit le signe de « x ». En effet, les puissances paires d’un nombre positif ou négatif sont toujours positives.

On a donc :    «  f ( +  ) = +  »      et    «  f ( -   ) =   +    »

N°2 : Dans les mêmes conditions que ci-dessus ; le polynôme :  «  f ( x ) =  x ³ – 3 x² + 1  » croît indéfiniment par valeurs positives , ou négatives en même temps que « x » ; En effet , son premier terme «   x ³ » est positif ou négatif avec « x », car les puissances impaires d’un nombre négatif sont négatives.

On a donc ,pour ce polynôme :    «  f ( +  ) = +  »      et    «  f ( -   ) =   -     »

Valeur d’une fraction rationnelle lorsque  « x »  tend vers l’ infini

Soit une fraction « y » dont les deux termes sont des polynômes en « x » de degrés quelconques  en « n »  et « p ».

 «  »

Quand « x » augmente indéfiniment, les polynômes du numérateur et du dénominateur augmentent indéfiniment. ( voir chapitre précédent ) , la fraction prend la forme indéterminée :   «  = ?   »  et on ne peut rien dire « a priori » de sa limite.

Décomposons les deux termes en produits, en mettant en facteur dans chacun d’eux la plus haute puissance de « x ».

Nous aurons : «  »

Quand « x » croît indéfiniment, toutes les fractions qui ont « x » , ou une puissance de « x »  au dénominateur tendent vers « 0 » (voir valeur remarquable d’une fraction ci-dessus)   et le second facteur tend vers la limite «  » différente de « 0 ».

Si « n » est égal à « p » :  le premier facteur   «  » est égal à « 1 », quel que soit « x » ; la limite de « y » est alors  «   »

Si « n » est plus petit que « p » :  le premier facteur   «  » est égal à   «  » et tend vers « 0 », et il en est de même de « y ».

Si « n » est plus grand  que « p » :  le premier facteur   «  » est égal à  « x ^u-p » et croît indéfiniment avec « x » , et il en est de même de « y ».Dans ce cas, pour des valeurs de « x » ; assez grandes en valeur absolue, « y »  a le signe de  « . x ^u-p  », ce signe  est celui de «  » , si « n » et « p » sont de même parité ; celui de  «  . x » , si  « n » et « p » sont de parités différentes.

Ainsi une fraction rationnelle de « x » croît indéfiniment en même temps que « x » , si son numérateur est de degré supérieur à celui de son dénominateur ; elle tend vers « 0 » si son numérateur est de degré inférieur à celui de son dénominateur ; enfin , elle a une limite finie et non nulle si ses deux termes sont de même degré ; cette limite est alors le quotient des coefficients des termes de plus haut degré au numérateur et au dénominateur,

Exemples :

N°1 : Soit la fraction :  quelles  sont les limites de « f (x) » lorsque « x » tend vers «  »

Elle croît indéfiniment avec « x » et prend le signe du quotient :  =. Elle augmente donc indéfiniment par valeurs positives   ou négatives en même temps que « x », et l’on a :   «  f ( +  ) = +  »      et    «  f ( -   ) =   -     »

N°2 : Soit la fraction : :     Quelles  sont les limites de « f (x) » lorsque « x » tend vers «  »

Lorsque « x » croît indéfiniment , la fonction a pour limite : «  » , quel que soit le signe de « x ». Ainsi, pour cette fonction :

«  f ( +  ) = +»      et    «  f ( -   ) =     »

Limite d’une fraction rationnelle dont les deux termes tendent simultanément vers « zéro »

Soit une fraction :       dont les deux termes sont des polynômes entiers en « x ».

Supposons que pour «  » , ces deux polynômes s’annulent en même temps.

«  f ( a ) = 0 »    et   «  F ( a )) = 0 »

la fraction prend alors la forme indéterminée :

Proposons nous de trouver la valeur limite de cette fraction quand « x » tend vers « a ».

Les polynômes «  f ( x ") »   et  « F ( x ) » s’annulant pour «  x = a » sont divisibles par  «  x – a » .

Divisons – les par «  x – a » , ainsi que les quotients successifs que nous trouverons, autant de fois qu’il sera possible .

Nous pourrons mettre les deux polynômes sous la forme :

  f ( x ")  =  ( x – a) ⁿ . q ( x) »   et  « F ( x ) =  ( x – a) ^p . Q ( x)» ; les derniers quotients  obtenus « q ( x) » et «Q ( x) » ne s’annulant plus pour «  x = a »

La fraction donnée ,s’écrira :

Quand « x » tend vers « a », le second facteur «  » tend vers la limite finie et non nulle «  »

Si « n » est égal à « p » le premier facteur  «  » est égal à 1,quelque soit « x » ; la limite de « y »  est «  »

Si « n » est plus grand que « p » le premier facteur  «  » est égal à   «  ( x – a ) ^{n – p} »  tend vers « 0 » quand « x » tend vers « a » ; et la limite de « y » est « 0 ».

Enfin, si « n » est plus petit « p », le premier facteur : «  »  croît indéfiniment quand « x » tend vers « a » , il en est de même de « y ».

Exemple :

La fraction : «  y =  » prend la forme «  » pour « x = 2 ». Quelle est la limite de « y » quand « x » tend vers « 2 »

En divisant les deux termes de la fraction par «  x – 2 » , on trouve :

« =  »

et la limite de « y » , pour « x = 2 »  est «  » .

N°2 : Trouver la limite de la fraction  «  »  quand « x » tend vers « -1 »

Les deux autres termes s’annulant pour « x – 1 » sont divisibles par « x +1 » ; de plus, le quotient du dénominateur par «  x + 1 » , «  x² - x -2 » s’annulant encore pour «  x = -1 » est divisible par « x + 1 » , et l’on a :

«   =   »

Quand « x » tend vers « -1 », le dénominateur tend vers « 0 » et la fonction « y » augmente indéfiniment. :  ( forme «   =  »)

Calcul de quelques limites.

N°1 : Quelle est la limite de  «  y =   quand « x » croît indéfiniment.

Si « x » augmente indéfiniment par « valeurs négatives » , le polynôme de degré pair « 2x² + 3 x -1 »  tend vers «  +  » ainsi que sa racine carrée ; «  - x  » tend vers «  +  » . Donc « y » augmente indéfiniment par valeurs positives.

Si « x » augmente indéfiniment par « valeurs positives » la fonction « y » se présente sous la forme « «   -   » , c'est-à-dire sous une forme indéterminée.

Cherchons à ramener l’expression à la forme : «  = ?   »  t pour cela , multiplions et divisons par la somme : «  »

Nous aurons :

«  »

et , en observant que le numérateur, produit d’une différence par une somme,est une différence de carrés.

«  »

«  »

Quand « x » tend vers «  +  » , cette fraction prend la forme : «  » suivant une méthode déjà suivie (voir : valeur d’une fraction rationnelle pour « x » infini. ». 

Divisons les deux termes par « x » ; il vient :  « 

Car il faut diviser le dénominateur par « x= » et , par suite, sous le premier radical par « x² »

Or , « x » augmentant indéfiniment , il reste :

(cette notation veut dire : limite de « y » égale……)

N°2 :  Quelle est la limite de  «    quand « x » tend vers « 0 » ?

Les deux termes s’annulent pour « x = 0 » et le rapport prend la forme «  » . Pour trouver sa limite , nous rendrons le numérateur rationnel en utilisant l’identité.

«  u²  - v² =  ( u – v) (  u² + u.v + v²)

Posons  «  x + 1 = u » ;  « = u » , et multiplions les deux termes de « y » par « u² + u.v + v² »

Nous aurons :

Développant le numérateur et supprimant le facteur « x » commun aux deux termes, il vient :

   en remplaçant maintenant « x » par  « 0 » , on trouvera :

Résumé :

On dit , qu’une fonction »y » d’une variable « x » tend vers une limite « b » lorsque « x » tend vers « a », si , lorsque « x » se rapproche de plus en plus de la valeur « a », les valeurs de « y » diffèrent de moins en moins de « b ».

La limite d’une somme de fonctions est égale à la somme de leurs limites.

De même , pour un produit , un quotient , une puissance , une racine.

Pour « x » infini, un polynôme se comporte comme son terme de plus haut degré et de même  , une fraction rationnelle se comporte comme le rapport des termes de degré les plus élevés.

Pour trouver la limite d’une fraction rationnelle dont les deux termes tendent simultanément vers zéro, on divise ces deux termes par le facteur commun qui les annulait à la fois.

TRAVAUX AUTO FORMATIFS

CONTROLE :

Relire le cours !!!!

EVALUATION :