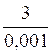COURS

Soit l’équation de la forme       

Discussion :

1°) si a est différent de 0 , , on peut diviser les deux membres de l’égalité par « a » , et on a « x =  » .il y a donc un nombre , et un seul , qui répond à la question.

2°) si « a » est nul et si « b » est différent de 0 ; quelle que soit la valeur de x , jamais  0 x ne pourra être  égal à b ; il n’y a pas de solution.

3°) si a est nul et si b est aussi nul  ; quelle que soit la valeur de x , l’équation sera toujours satisfaite ; il y a une infinité de solutions.

En résumé :

Remarque 1 :

Considérons les fractions :

On voit que , le numérateur d’une fraction étant constant , si le dénominateur de la fraction devient de plus en plus petit , la valeur de la fraction  devient de plus en plus grande et grandit indéfiniment  quand le dénominateur diminue indéfiniment ; considérons  x = ; b restant fixe et différent de 0 , si                  diminue indéfiniment  , la valeur de « » grandit indéfiniment ; on dit alors que la valeur de       , qui est dénuée de sens arithmétique , représente une valeur infiniment grande ; on la représente par le signe ¥ , que l’on appelle l’infini ; et on dit que  , quand b ¹ 0 , est le symbole de l’infini.

Remarque 2 :        « symbole de l’indétermination. »

Lorsque , dans  :    « a »  étant égal  à 0 , « b » est aussi égal à 0 , on a vu qu’il y a une infinité de solutions , que l’équation est  indéterminée , si on garde la notation x = ; même de ce cas , ce qui n’est qu’une  forme , et non pas alors une opération arithmétique , la valeur de « x » se  présente sous la forme   et on sait qu’elle est indéterminée , on est conduit alors à dire que  est le symbole de l’indétermination.