Pré requis:

Le rectangle
Le losange
Les quadrilatères

ENVIRONNEMENT du dossier:

Index « warmaths »

Objectif précédent : Le carré (primaire) Quadrilatère : Le carré (cours )

Objectif suivant : 1°) Le périmètre du carré 2°) Le trapèze 3°) Calculs : le périmètre (dos 81) 4°) La surface d’un carré.

1°) Info générales sur les principales figures géométriques. (niv V)

Le quadrilatère : DOSSIER : LE CARRE ( classe 4^ème collège )

	Définitions
	Les propriétés
	Comment identifier un carré
				ACTIVITES
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité Série 1 : Série 2 : Activité d’études préalables  :dos 80 Série 3 : situations problèmes. Sérié 4 : le carré en arithmétique	Corrigé Contrôle	Corrigé évaluation

Fiche : Le carré

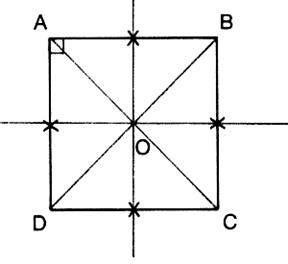
On appelle « carré »tout quadrilatère qui est à la fois losange et un rectangle.

Activité 1 :

Tracez les axes de symétrie du carré ci-contre.

Activité 2 :

Dites « oralement » comment on peut prouver qu’un quadrilatère est un carré.

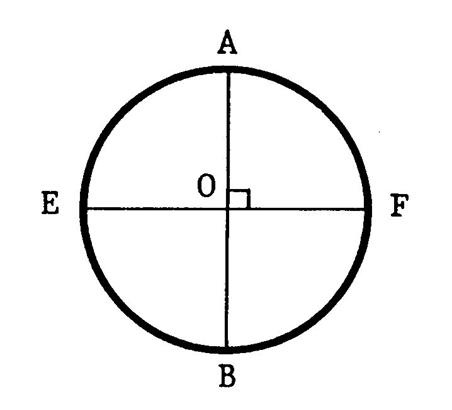
Activité 3 :

Ci –contre ,on vous donne un cercle de centre « O » et deux diamètres perpendiculaires [AB] et [ EF].

Démontrez que « AEBF » est un carré.

RESUME :

Définitions : Rectangle ayant deux côtés consécutifs isométriques (1) Ou Losange ayant un angle droit (2) AB = BC = CD= DB = a = = = = 90° le carré est un polygone régulier .	Propriétés : - ce sont les propriétés du rectangle et du losange ; - 4 axes de symétrie : les 2 du rectangle et les 2 du losange - 1 centre de symétrie : c’est le point de concours des axes de symétrie (voir + : la symétrie centrale) - (la mesure des diagonales = d = a )
Pour l’ Identification : utilisation de (1) ou (2) ( voir la démonstration en géométrie @)

TRAVAUX AUTO – FORMATIFS.

CONTROLE :

Qu’est qu'un carré?

Quelles sont les propriétés du carré ?

EVALUATION

1°) Tracer un carré dont un coté mesure 4 cm.

2 ) Tracer un carré sachant que sa diagonale est égale à 4,5 cm

3 ) On donne un carré ABCD ayant pour coté 5 cm. Tracer à l'intérieur du carré , un quadrilatère EFGH tel que ses 4 sommets soient situés sur les cotés du carré et que l'on ait par ailleurs:

BE = BF = DG = DH = 3 cm

4) On donne un carré de 6 cm de coté . Tracer à l'intérieur de ce carré un losange ayant 5 cm de coté et tel que sa grande diagonale coïncide avec l'une des diagonales du carré.

5°) Tracer :

Carré de côté AB = 43 mm

Carré de diagonale AC = 52 mm

En plus : carré de périmètre p = 10 cm

En plus : carré d’aire A = 1225 mm²