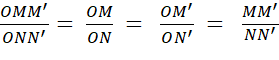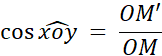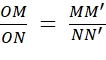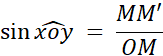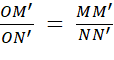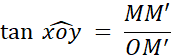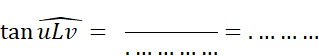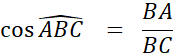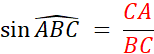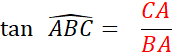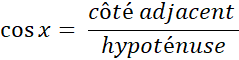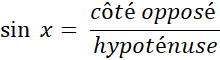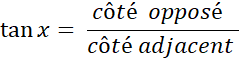Fiche 1   : Relations trigonométriques  d’un angle aigu

Fiche 2 : Dans le triangle rectangle.

Fiche 3 : Construction d’un angle aigu connaissant son cosinus , son sinus ou sa tangente.

Fiche 1   : Relations trigonométriques  d’un angle aigu

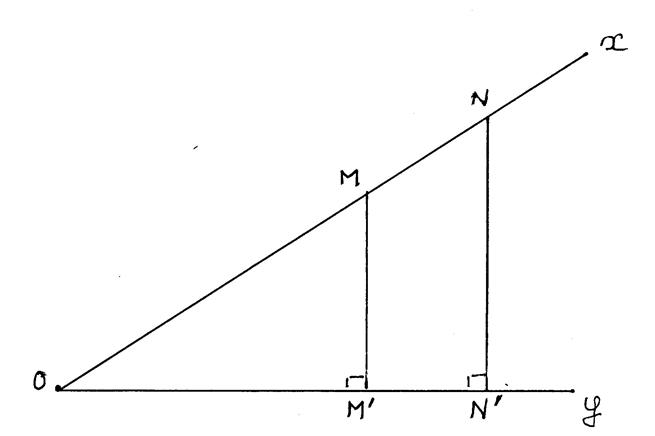
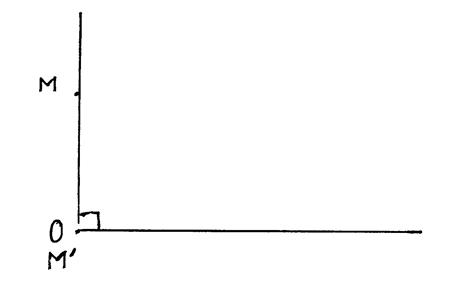
Voici ci-contre un angle aigu

« M » et « N » sont des points quelconques de [ Ox .

« M’ » et « N’ » sont les  projetés orthogonaux de « M » et « N » sur [ Oy.

Grâce au théorème de Thales on peut écrire :

Partant de  on en déduit

Quelle que soit la position de « M »  sur [ Ox   , le quotient  a toujours la même valeur.

Vous reconnaissez le cosinus de l’angle

Partant de   on en déduit que 

Quelle que soit la position de « M »  sur [ Ox   , le quotient  a toujours la même valeur.

Ce nombre est appelé le sinus de l’angle  

Partant de   on en déduit que 

Quelle que soit la position de « M »  sur [ Ox   , le quotient  a toujours la même valeur.

Ce nombre est appelé le tangente  de l’angle

Cas particuliers :

Si l’angle  ; « M’ » et « M » sont confondus.

Donc  «  MM’ = 0 »    et    «  OM = OM’ »

Cos 0° =

Sin 0° =

Si l’angle  ; « M’ » et « M » sont confondus avec « O ».

Donc  «  OM’ =……… »    et    «  MM’ = OM »

Cos 90° =  ……..

Sin 90° = …….

Attention : tan 90°  n’existe pas ( expliquez pour quoi verbalement )

Activité :

Après avoir fait les constructions nécessaire, déterminez approximativement :

 ; 

Vous en déduisez que

Contrôlez  en mesurant sur la feuille l’angle 

Fiche 2 : Dans le triangle rectangle.

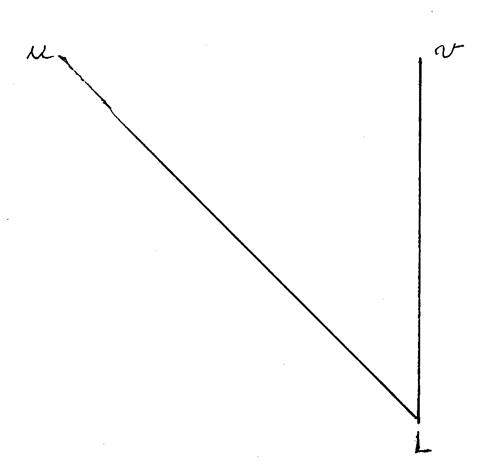
Voici un triangle « ABC » rectangle en « A » .

Considérons l’angle  .

« C » est un point de la demi-droite [ BC.

Il se projette orthogonalement en « A3 sur [ BA.

On retrouve alors  la situation sur la fiche 1.

On peut écrire .

Vocabulaire :

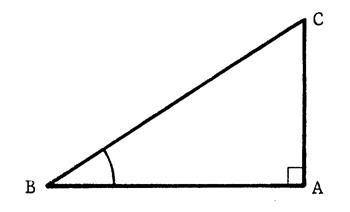
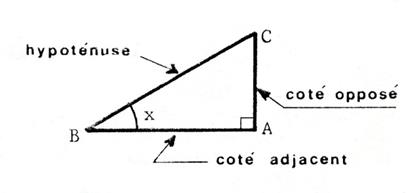
Dans le triangle rectangle en « A ».

[BC] est l’hypoténuse,

[ BA]  est appelé « côté adjacent à l’angle  »

( sous entendu , côté adjacent qui n’est pas hypoténuse)

[ CA ] est appelé « côté opposé à l’angle  »

Avec ces notations , nous écrirons schématiquement :

« x » désignant un angle aigu d’un triangle rectangle.

Remarque :

Puisque dans tout triangle rectangle , l’ hypoténuse est le plus grand des côtés , alors le sinus et le cosinus d’un angle aigu sont des nombres inférieurs à « 1 ».

Fiche 3 : Construction d’un angle aigu connaissant son cosinus , son sinus ou sa tangente.

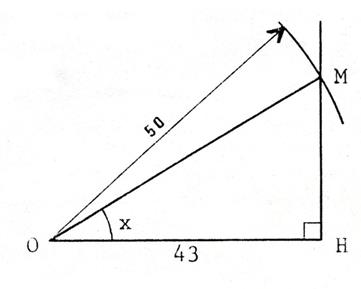
Exemple :

Construisons un angle « x » sachant que

Tout revient à construire un triangle « OMH » rectangle  en « H », tel que   .   et   

On peut prendre « OH = 43 mm »  et « OM = 50 mm ».

On a alors 

Donc    est l’angle cherché.

Activité :

Construisez un angle « y » sachant que

Construisez un angle « z » sachant que

Remarque :

Tout nombre compris entre « 0 »   et « 1 » peut être considéré comme le sinus ou le cosinus d’un angle aigu.

Tout nombre positif peut être considéré comme la tangente d’un angle aigu.