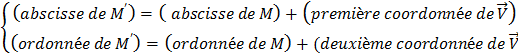|
|
Fiche 1 :
on revoit les Prérequis : voir en classe de 4ème
|
Translation
et vecteurs.
|
|
|
|
|
|
|
|
Rappels :Translation
et vecteur :
|
|
|
|
Le dessin ci-contre illustre le fait que «
F’ » et l’image de « F » dans la translation de vecteurs : 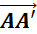
· Pour comprendre cette situation , imaginez
que l’on a déplacé en bloc
« F » pour l’amener sur « F’ » de telle sorte que
ce déplacement se fasse :

|
|
|
|
|
Dans cette
translation, tout point « M » de « F » a pour image « M’ » de
« F’ » tel que :
|
|
|
|
|
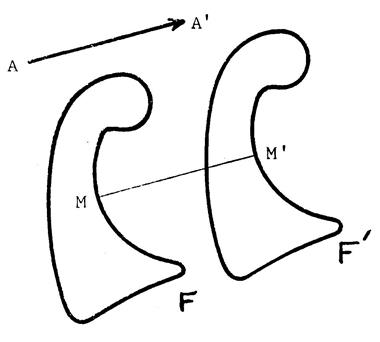
-
(MM’) a la direction
de (AA’) c'est-à-dire (MM’) est parallèle à
( AA’)
|
|
|
|
|
-
Le sens de
« M » vers « M’ » est le même que le sens de « A » vers
« A’ »
|
|
|
|
|
-
Les longueurs « MM’ » et « AA’ » sont égales.
|
|
|
|
-
|
|
|
|
-
Cette direction
|
|
|
|
|
-
Ce sens
|
Caractérisent
le vecteur de la translation.
|
|
|
|
-
Cette longueur
|
|
|
|
|
Le vecteur 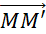 définit la même translation
des définit la même translation
des 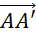 ; on écrit alors : ; on écrit alors : 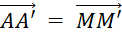
|
|
|
|
A retenir :
|
|
|
|
|
( AA’) et ( MM’) ont même direction , c'est-à-dire ( AA’)
// ( MM’)
|
|
|
|
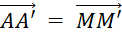 signifie signifie
|
Le sens de « A » vers « A’ »
est le même que le sens de « M » vers
« M’ »
|
|
|
|
|
Les longueurs
« AA’ » et « MM’ » sont égales.
|
|
|
|
|
|
|
|
Dessin
représentant un vecteur :
|
|
|
|
Pour représenter graphiquement un vecteur, on
dessine un segment fléché.
|
|
|
|
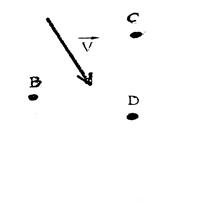
Exemple : ( voir
ci-contre)
La droite
(TS) donne la direction du vecteur 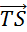 . .
La flèche indique le sens
du vecteur.
« T » est l’origine et « S »
l’extrémité du couple ( T , S ) ( appelé :
bipoint)
La longueur de
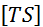 donne la longueur du vecteur. donne la longueur du vecteur.
|

|
|
|
|
|
|
|
|
Nota : il y a une infinité de couples de
points correspondant au même vecteur.
Il y a donc une infinité de façons de représenter
un vecteur.
(voir ci-contre)
|
|
|
|
|
Notation : On a désigné par 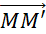 le vecteur correspondant au
couple de points noté ( M , M’ ) ;
mais on peut désigner un vecteur par une seule lettre , par exemple : le vecteur correspondant au
couple de points noté ( M , M’ ) ;
mais on peut désigner un vecteur par une seule lettre , par exemple : 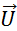 ; ; 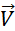 ; …. ; ; …. ; 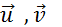 etc. ………. etc. ……….
Dire que « B’ » est l’image de
« B » dans la translation de vecteur 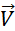 ; c’est dire que : …… ; c’est dire que : ……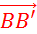 ………..= …… ………..= ……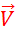 …………. ………….
|
|
|
|
|
|
|
|
Activité 1 :
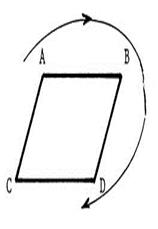
Dessinez
« B’ » ; « C’ » ; « D’ » des
points « B » , « C » , « D » dans la translation
de vecteur 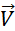 . .
|
|
|
|
|
|
|
|
|
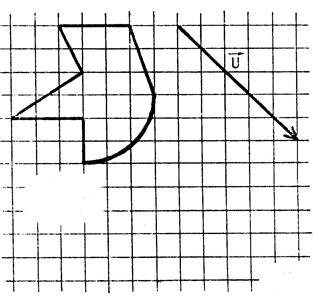
Activité 2 :
Dessinez l’image de la figure ci-contre dans la translation de vecteur
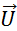 . .
|
|
|
|
|
Conseil : nommez les intersections
par des points ; puis faire glisser chaque point suivant la direction du
vecteur « u » sur une longueur « longueur du segment de
« u »..
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fiche 2 : Vecteurs égaux et parallélogramme.
|
Info ++@...
|
|
|
|
|
|
|
|
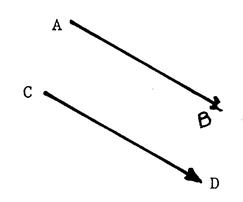
« A » ,
« B » , « C » , « D » sont quatre points non
alignés .
Considérons le cas où les couples ( A, B) et (C,D )
représentent le même vecteur. On a alors 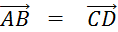
Vous savez que 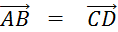 signifie que : signifie que :
|
|
|
|
|
|
|
|
|
|
-
(AB) et (CD)
sont parallèles .
|
|
|
|
|
-
Le sens de
« A » vers « B » est le même sens de « C »
vers « D » .(
C’est à dire que le quadrilatère n’est pas
croisé
).
|
|
|
|
|
-
AB = CD
|
|
|
|
|
|
|
|
Considérons
le quadrilatère « ABCD » . ON vient de dire qu’il est non croisé et
qu’il a une paire de côtés parallèles et
de même longueur.
C’est
donc un parallélogramme.
On
dira alors : si 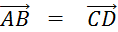 alors « ABCD » est
un parallélogramme. alors « ABCD » est
un parallélogramme.
|
|
|
|
Inversement : Démontrez oralement que : si « ABCD » est un parallélogramme
alors 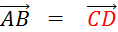 . .
|
|
|
|
|
|
|
|
Remarque :
Dans le cas où « ABCD » sont alignés , nous dirons que le
quadrilatère « ABCD » est un parallélogramme aplati.
|
|
|
|
|
|
|
|
|
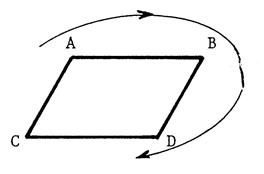
Théorème :
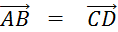 signifie que « ABDC » est un
parallélogramme. signifie que « ABDC » est un
parallélogramme.
|
|
|
|
|
Attention : ne vous trompez pas dans la disposition des
points : « ABDC » et non
pas « ABCD »
|
|
|
|
Activité :
complétez :
|
|
|
|
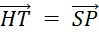 signifie « HTPS »
est un parallélogramme. signifie « HTPS »
est un parallélogramme.
|
|
|
|
Activité
n° … :
|
|
|
|
Dans
chacun des 6 cas , placez le point « D » tel que : 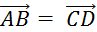
|
|
|
|
|
|
|
|
|
|
|
|
v
Sachant
que « ABCD » est un parallélogramme , vous pouvez écrire les 4 égalités vectorielles :
|
|
|
|
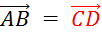
|
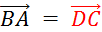
|
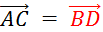
|
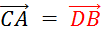
|
|
|
|
Et
inversement , si l’une de ces égalités est vraie alors « ABDC » est un parallélogramme.
|
|
|
|
|
|
|
|
Théorème :
« A »,
« B » , « C » , « D » étant des points du plan, les égalités
suivantes sont équivalentes :
|
|
|
|
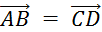
|
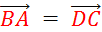
|
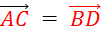
|
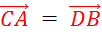
|
|
|
|
 corrigé corrigé
|
|
|
|
|
|
|
|
Vecteurs
opposés :
|
|
|
|
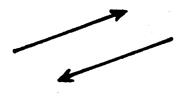
Des
vecteurs qui ont même direction et même longueur mais de sens contraires sont
dits « opposés ».
|
|
|
|
|
Exemple :
« A » et « B » étant des points quelconques , 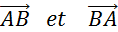 sont
« opposés ». sont
« opposés ».
|
|
|
|
|
|
|
|
Vecteur nul :
|
|
|
|
A
partir d’un couple (A,A’) de points
distincts, on a pu définir une
translation et le vecteur 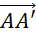 associé à cette translation. associé à cette translation.
Si
les points « A » et
« A’ » sont confondus alors ,dans la translation
correspondante, chaque point est confondu avec son image. Le vecteur de cette
translation a pour longueur « 0 »
et sa direction n’est pas définie.
Ce
vecteur est appelé le vecteur nul. On le note : 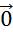
|
|
|
|
|
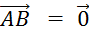 signifie que « signifie que «  » »
|
|
|
|
|
|
|
|
|
Fiche
3 : Milieu d’un segment.
|
Info @ calcul sur le milieu..
|
|
|
|
|
|
|
|
Voici
ci-contre un segment 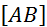 et son milieu « M ». et son milieu « M ».
Comparons
les vecteurs 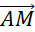 et et 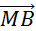 . .
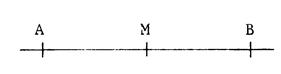
« M »
est le milieu de 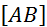 signifie : signifie :
|
|
|
|
|
|
|
|
|
|
-
« M »
est situé sur (AB ) c'est-à-dire ( AM
) a même direction que ( MB). ; AM  MB MB
-
« M »
est entre « A » et « B ». ( Le sens de « A »
vers « M » est le même que le sens de « M »
vers « B » .
|
|
|
|
Ce
qui revient à dire que :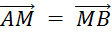
|
|
|
|
D’où
le théorème :
« M »
est le milieu de 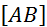 signifie que : signifie que :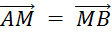
|
|
|
|
|
|
|
|
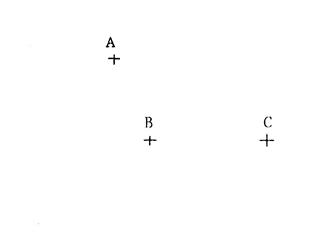
Activité
1 :
|
|
|
|
Ci-contre
, on vous donne trois points « A » , « B » , «
C » distincts.
Placez
le point « E » tel que 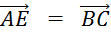
Placez
le point « F » tel que 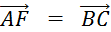
Démontrez
que « A » est le milieu de 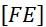
|
|
|
|
|
Activité
2 :
|
|
|
|
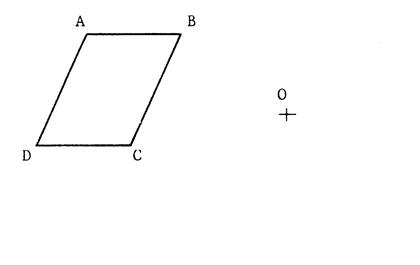
Voici
un parallélogramme @ « 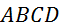 » et
un point « O ». » et
un point « O ».
Placez
les points « M » , « N » , « P » , «
R » tels que :
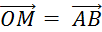 ; ; 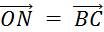 ; ; 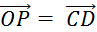 ; ; 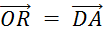
Démontrez
que « 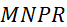 » est
un parallélogramme. » est
un parallélogramme.
|
|
|
|
|
|
|
|
|
Fiche
4 : Situation problème.
|
|
|
|
|
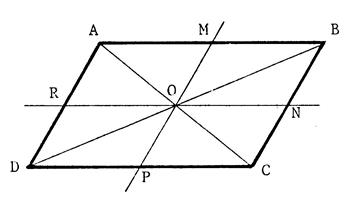
«  » est
un parallélogramme de centre
« O ». » est
un parallélogramme de centre
« O ».
On
trace par « O » la parallèle à ( AD ) et ( BC )qui coupe (AB ) en
« M » et ( DC ) en « P ».
On
trace par « O » la parallèle à ( AB ) et ( DC ) qui coupe ( AD ) en
« R » et ( BC ) en « N ».
|
|
|
|
|
1°)
Démontrez ( verbalement , oralement ) que « M », « N » ,
« P », « R » sont
les milieux des côtés du parallélogramme.
|
|
|
|
2°)
En utilisant les points de la figure , écrivez toutes les égalités
vectorielles possibles . (sauf les égalités de vecteur nul).
Vous
démontrerez oralement ces égalités .
|
|
|
|
|
|
|
|
Instructions.
Recherchez
tous les parallélogramme de la figure.
N’oubliez
pas les vecteurs tels que : 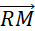 et et 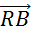 . .
Pour
vous simplifier la tâche , on a fait deux colonnes :
Dans
l’une vous écrirez une égalité vectorielle et dans l’autre vous écrirez
l’égalité des vecteurs opposés.
|
|
|
|
|
|
|
|
Exemple
|
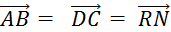
|
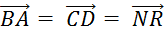
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fiche
5 Translation et coordonnées.
|
Translation…@….
|
|
|
|
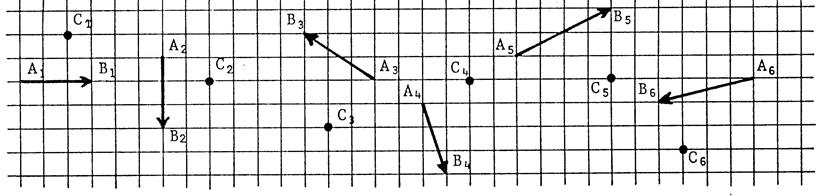
On a
représenté ci-dessous trois fois la
figure « F ».( le polygone «  »
)avec le même système d’axes de coordonnées d’origine « »
)avec le même système d’axes de coordonnées d’origine «  ». ».
Etudes
de 3 cas :
|
|
|
|
Prérequis :
retrouver les coordonnées des points du polygone « 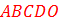 ». ».
|
|
|
|
Cas
1 :
|
|
|
|
|
Dessinez
l’image de la figure « F » dans la translation correspondant au
vecteur donné : 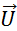 . .
Vous
appelez :
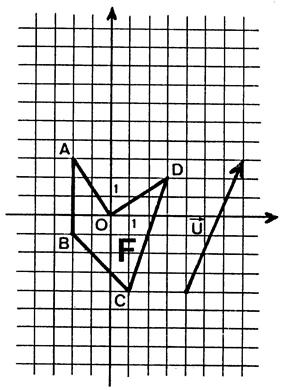
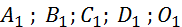 les images de les images de 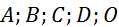 dans la translation de vecteur dans la translation de vecteur
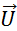 . .
Complétez
le tableau donnant les coordonnées des images
|
|
|
|
|
A(-2
;3 )
|
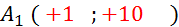
|
|
B
( -2 ; -1)
|
|
|
C
( 1 ; -4)
|
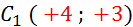
|
|
D
( 3 ;2 )
|
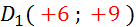
|
|
O
( 0 ;0 )
|
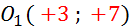
|
|
|
Ajouter
à l’abscisse +3 , et à l’ordonnée +7
|
|
|
|
|
|
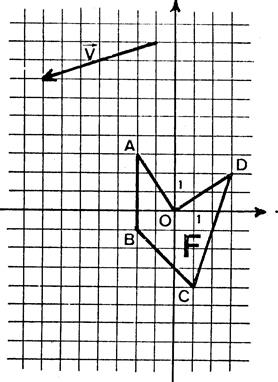
Cas
2 :
|
|
|
|
|
|
|
Dans
chacun des cas , Dessinez l’image de la figure « F » dans la
translation correspondant au vecteur donné : 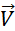 ; ;
|
|
|
|
|
A(-2
;3 )
|
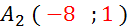
|
|
B
( -2 ; -1)
|
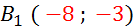
|
|
C
( 1 ; -4)
|
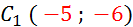
|
|
D
( 3 ;2 )
|
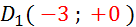
|
|
O
( 0 ;0 )
|
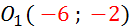
|
|
|
Ajouter
à l’abscisse - 6 , et à l’ordonnée -2
( on descend le point de « 2 » case et on le déplace à gauche de
« 6 » cases
|
|
|
|
|
|
Cas
3 :
|
|
|
|
|
|
|
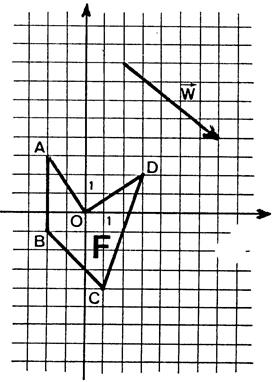
Dessinez
l’image de la figure « F » dans la translation correspondant au
vecteur donné : 
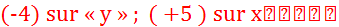
|
|
|
|
|
E:\warmaths_13\warmaths\MATH\geometr\quadrlla\p4_parallelogramme_def_propriete_milieu_symetrie_central.htmA(-2
;3 )
|
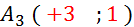
|
|
B
( -2 ;-1 )
|
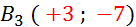
|
|
C
( 1 ; -4)
|
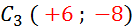
|
|
D
( 3 ; 2 )
|
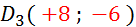
|
|
O
( 0 ;0 )
|
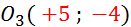
|
|
|
|
|
|
|
|
|
|
Comparez
, dans les 3 cas, les coordonnées de chaque point avec les coordonnées de son
image.
Vous
constatez alors que :
A
partir des coordonnées d’un point ,
pour obtenir les coordonnées de l’image de ce point,
-
Dans
la translation de vecteur 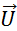 , à l’abscisse on ajoute …( + 3 ) ., à
l’ordonnée on ajoute …( + 7 ).. , à l’abscisse on ajoute …( + 3 ) ., à
l’ordonnée on ajoute …( + 7 )..
-
Dans
la translation de vecteur 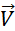 , à l’abscisse on ajoute …( - 6 ) .., à
l’ordonnée on ajoute …( - 2 )….. , à l’abscisse on ajoute …( - 6 ) .., à
l’ordonnée on ajoute …( - 2 )…..
-
Dans
la translation de vecteur 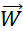 , à l’abscisse on ajoute …( + 5 )….., à
l’ordonnée on ajoute …(- 4)….. , à l’abscisse on ajoute …( + 5 )….., à
l’ordonnée on ajoute …(- 4)…..
|
|
|
|
Aussi :
Le
nombre « 3 » que l’on a
ajouté à l’abscisse est appelé la « première coordonnée » du
vecteur 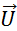 , ,
Le
nombre « 7 » que l’on a
ajouté à l’ordonnée est appelé la « deuxième coordonnée » du
vecteur 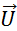 , ,
(
3 ; 7 ) est appelé le « couple de coordonnées » du vecteur 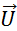 . On
écrira . On
écrira 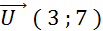 . .
Complétez
de même : 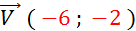 ; ; 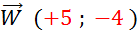
Ce
que vous avez étudié sur trois exemples
est vrai dans le cas général.
|
|
|
|
|
|
|
|
Théorème :
Ayant
choisi dans le plan un système d’axes de coordonnées , « M » étant un point quelconque et
« M’ » son image dans la translation de vecteur 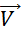 , ,
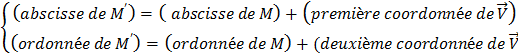
|
|
|
|
Revoir
le cours sur l’addition de deux nombres relatifs@…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|