Exemples : l’étude statistique portant sur la population de joueurs dont les caractères étudiés sont le poids et la taille , pour occupé un poste dans une équipe est une série à deux variable.

2- Nuage de points associé :

A chaque caractère est associé un couple de valeurs. L’ensemble des couples représentés dans un repère cartésien, n’étant alignés , constitue un ensemble de points dispersés.

Généralement cet ensemble est partagé en deux nuages , auquel on déterminera un point moyen.

Le point moyen d’un nuage de points a pour :

- abscisse : la moyenne des abscisses des points constituant le nuage ;

- ordonnée, la moyenne de leurs ordonnées.

3°) Droite d’ajustement affine.

Info+

L’intérêt d’une telle étude statistique réside dans la recherche du lien éventuel existant entre les deux caractères étudiés.

On peut tenter de mathématiser cette liaison établissant une loi permettant de prédire avec un faible degré d’incertitude la valeur d’un caractère en fonction de la valeur de l’autre caractère.

L’ un des modèles mathématiques les plus simples est la fonction affine dont la représentation graphique est une droite.

Exemple : Ajustement linéaire : passant par un ensemble de points sensiblement alignés. (méthode qui intéresse les séries Statistiques à deux variables)

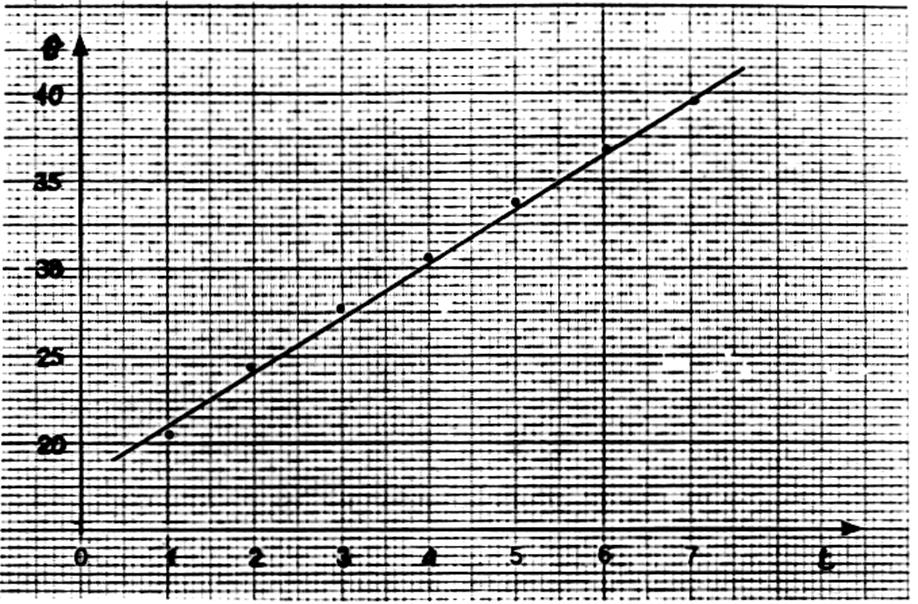
Exemple d’application : on chauffe l’eau contenu dans un bécher à l’aide d’un thermoplongeur. On note la température de l’eau toutes les minutes.

Durée t en min.	1	2	3	4	5	6	7
q en °C	20,5	24,3	27,6	30,5	33,7	36,8	39,5

Sur un graphique , nous portons en abscisse les durées « t » et en ordonnée la température correspondante « q ».

Observation : nous constatons que les points sont « sensiblement » alignés : les températures sembles varier en fonction de la durée de chauffage à prés comme une fonction affine. On décide alors « d’ajuster » une droite à cet ensemble de points. Pour cela, on utilise dans la pratique deux méthodes , indifféremment : « la méthode Mayer » ou « la méthode des moindres carrées ».

1- Méthode de Mayer ou méthode double moyenne.

¨ création de deux groupes de points. Les valeurs de « t » étant ordonnées, on partage l’ensemble de points en deux groupes d’égales importance ( à une unité près). Nous obtenons :

Premier groupe	( 1 ; 20,5)	(2 ; 24,3)	( 3 ; 27,6)	( 4 ; 30,5)
Deuxième groupe.	( 5 ; 33,7)	( 6 ; 36,8)	( 7 ; 39,5 )

( on aurait pu prendre trois points pour le premier groupe et quatre pour le second)

¨Pour chaque groupe, on calcule les coordonnées du point moyen ;

Remarques :ces points sont aussi appelés : barycentres et la droite qui passe par ces deux points est appelée : droite de Mayer.

- Coordonnée du point moyen du premier groupe :

;

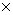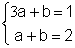
- Coordonnée du point moyen du second groupe :

;

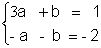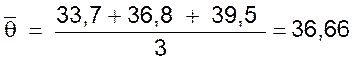
¨ On trace la droite passant par les deux points moyens : ( 2,5 ; 25,725) et ( 6 ; 36,66)

¨Cherchons l’équation de cette droite :

Le coefficient directeur est :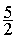

D’ où la droite q = 3,12 t + b

Si « t = 2,5 » , alors « q = 25,725 » ; d’où 25 , 725 = 3,12 fois 2,5 + b

Et 25,725 - 7,8 = b ; soit « b = 17,925 »

L’équation cherchée est : q = 3,12 t + 17,925

Commentaires :

Par la méthode de calcul, la courbe d’ajustement est forcément une droite et non plus une ligne brisée .Connaissant les coordonnées des deux points d’une droite, il est alors facile de déterminer l’équation de la droite de Mayeur. (de la forme y = ax+b)

Cette méthode , évidemment simple , à l’inconvénient d’être approximative, surtout quand le nombre des points composant le nuage est élevé et que leurs valeurs sont très disparatres.

2- Méthode des moindres carrés. ( lire « somme »)

1° principe : la méthode est basée sur le principe qu’il faut réduire au maximum les écarts verticaux entre les valeurs observées et leurs valeurs théoriques fournies par la droite d’ajustement.

Le but : minimiser ( Ecart ₁ + écarts₂ + …….+ écarts _n )

que nous écrivons : min Þ ( des écarts)

L’écart de définit comme mesurant algébriquement la différence entre la valeur observée et la valeur ajustée.

Ecart ₁ = y ₁ - y’₁ Ecarts₂ = y ₂ - y’₂

Cette différence peut être positive (écarts₂ ) , négative (Ecart ₁ ) , ou nulle ( si les valeurs théoriques et observées sont confondues) . Pour élimer ce problème de signe et faire en sorte que la sommation de ces écarts ne se traduise pas par une compensation quand ils sont de signes contraires on les élève au carré, ce qui les rend tous positifs.

Nous cherchons donc à : Min Þ ( écarts)²

L’expression d’un écart quelconque peut s’écrire y ₁ - y’₁donc la droite la plus représentative est celle pour laquelle la somme des carrés des écarts est minimale, d’où le nom de méthode des moindres carrés.

2°) Les paramètres « a » et « b » de la droite des moindres carrés.

La droite doit minimiser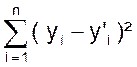

En développant cette expression et en remplaçant « y’_i » par sa valeur en fonction de « x _i » , on arrive à un trinôme du second degré qui sera minimum lorsque sa dérivée sera nulle.

On arrive ainsi à définir le coefficient angulaire « a » et le paramètre « b » de la droite des moindres carrés.

La droite que l’on obtient par cette méthode est celle qui rend minimum la somme des carrés entre les points observés et les points de la droite ayant même abscisse. Elle est appelée « droite de régression » de « y » en « x ».

TRAVAUX FORMATIFS :

CONTROLE

1°) Donner la procédure qui permet de déterminer l'équation d'une droite dont on connaît le coefficient directeur et un point de la droite.

On connaît « a », il suffit de déterminer « b »

La droite passe par le point A ( x₁ ; y₁) ; on a y₁ = a x₁ + b

On en déduit la valeur de « b » : b = y₁ - a x₁

(le calcul terminé , il suffit de remplacer « b » dans l’équation de départ par la valeur trouvée)

2°) Donner une procédure qui permet de déterminer l'équation d'une droite dont on connaît deux couples de nombres.

Procédure :

1°) On calcule « a » : tel que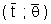

2°) on se fixe (choisi) un point « A » ou « B » , on prend ses coordonnées

3°) On connaît « a », il suffit de déterminer « b »

La droite passe par le point A ( x₁ ; y₁) ; on a y₁ = a x₁ + b

On en déduit la valeur de « b » : b = y₁ - a x₁

(le calcul terminé , il suffit de remplacer « b » dans l’équation de départ par la valeur trouvée)

EVALUATION

N°1 : Déterminer l’équation de la droite de coefficient directeur « -0,5 » et passant par le point A ( 4 ; -1) ; à vérifier par le tracé.

L’équation est de la forme y = a x + b ,

Puisque « a » = -0,5.

Soit y = - 0,5 x + b (1)

Nous avons les coordonnées de A « x » = 4 ; y = -1

On remplace dans l’équation (1) :

-1 = 0,5 fois 4 + b

soit -1 = -2 + b

d’où après transformation : « b » = 1

en conclusion : l’équation cherchée est y = - 0,5 x + 1

( à vérifier par la résolution graphique)

N °2 :Déterminer l ’équation de la droite passant par les points A ( -2 ;1) et B ( 3 ; 3) ; à vérifier par le tracé.

1°) on calcule « a » :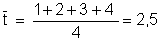

2°) L’équation est de la forme y = a x + b

y = 0,4 x + b

3°) d’après l’ énoncé ,en « A » pour x = - 2 nous devons avoir y = 1

1 = 0,4 fois (-2) + b

1 = - 0,8 + b

1 + 0,8 = b

d’ où b = 1,8

4°) L’équation cherchée est y = 0,4 x + 1,8

Nota : on aurait pu prendre les coordonnées du point « B », nous serions parvenu au même résultat. (à vérifier par le graphique)

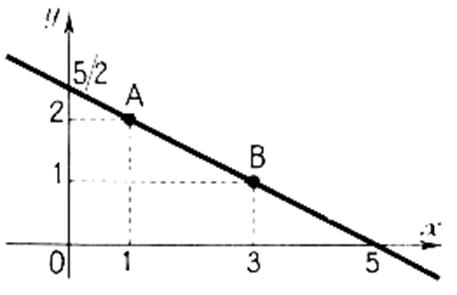
N° 3 Déterminer l'équation de la droite définie par deux points A ( 1 ; 2 ) et B ( 3 ;1 ) ; à vérifier par le tracé. .

l'équation est de la forme y = a x + b .

Ecrivons que les coordonnées de A ;puis celles de B , vérifient cette équation .

Nous obtenons :

Pour A ( x = 1 et y = 2 ) ; nous obtenons : 2 = a 1 + b ;soit (1) a + b = 2

Pour B ( x = 3 et y = 1 ) : nous obtenons : 1 = a 3 + b ; soit ( 2) 3a + b = 1

Les relations ( 1) et (2) représentent la même équation ; elles permettent de calculer "a" et "b"

Commentaire : Nous sommes en présence d’un système de deux équations que l’on décide de résoudre par la méthode de l’addition.( voir résoudre le système de (1) et (2) )

soit le système : ;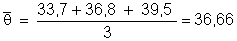

pour résoudre ce système on décide de multiplier « a + b = 2 » par - 1 , on peut ainsi remplacer dans le système « a + b = 2 » par « - a - b = - 2 »

nous avons le nouveau système :

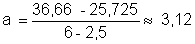
on additionne terme à terme dans les deux membres :

3a - a = 2a ; b - b = 0 ; 1 - 2 = -1 ;

Le résultat de l’addition des deux équations terme à terme nous donne donc 2a +0 = -1

on en déduit que « a » = oua = - 0,5

on en déduit b = = 2,5;

L équation de la droite AB est donc : 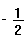ou y = - 0,5 x + 2,5