les séries statistiques à une ou deux variables

 

 Pré requis :

Les Statistiques  info

« Effectifs » et « fréquences »

ENVIRONNEMENT du dossier:

Index        

Objectif précédent :

Info sur les Séries statistiques  

Objectif suivant :

1°) Suite sur la série à deux variables.

tableau     3c

liste des cours

 

DOSSIER : Les SERIES STATISTIQUES à 1 ou  2 VARIABLES « quantitatives ».

 

TEST

           

COURS

               

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

                       

 

Corrigé Contrôle 

Corrigé évaluation 

 

 

COURS

 

I )Série statistique  quantitatif à une variable :

 

Exemples 

I )  Pour lancer une fabrication de vêtements , on désire avoir une information sur la mesure  des tailles  d’individus d’une même classe d’age .

On prend un échantillon  de  30 individus recensés :

Relevée des mesures : (réponses brutes)

 

171

158

163

174

177

165

176

179

175

182

168

173

180

177

160

185

177

187

167

190

173

167

175

182

172

178

184

171

179

169

 On range ces données par classes :

 

Limites des classes

 

Effectifs: ni

158-162

158 ; 160

n1 =  2

163-167

163 ;165 ;167 ;167

n2 =  4

168-172

168 ;171 ;171 ;169 ;172

n3 =  5

173-177

173 ;173 ;174 ;175 ;175 ;176;177 ;177 ;177

n4 =  9

178-182

178 ;179 ;179 ;180 ;182 ;182

n5 =  6

183-187

184 ;185 ;187

n6 =  3

188-190

190

n7 =  1

 

 

A ces mêmes élèves ont leur pose deux autres questions :

Ce  qui signifie que nous allons avoir deux autres séries statistiques :

1°)  Combien de temps , en minutes , avez vous écouté la radio le week-end dernier ?                               

 

Seconde série statistique :

150

130

185

180

220

200

235

120

195

200

160

90

170

180

140

160

100

190

190

230

185

180

210

205

180

200

200

160

220

230

2°) Combien possédez vous de récepteurs d’informations (radio , téléviseur , ordinateur , chaîne ,…) ?                    

 

Troisième  série statistique :

1

2

2

3

1

5

7

5

4

4

1

3

1

1

1

2

2

2

3

5

2

3

3

5

4

4

4

3

3

3

 Quatrième série statistique :

Le tableau des données ci dessous donne les résultats obtenus par un groupe d’élèves ( 25 )  lors d’un devoir de mathématique :

11

15

8

10

12

6

13

12

5

12

6

8

9

17

7

11

10

15

9

8

10

13

10

12

12

 

 

  

  II )  Série statistique  quantitatif à deux variables :

%ºInfo plus.

 

Définition:

Une série  statistique à deux variables est une série pour laquelle deux caractères mesurables sont relevés pour chaque individu.

 

Exemple :  tableau de relevées

Individu

a

b

c

d

e

f

g

h

k

l

Masse (  en kg)

98

102

103

103

107

109

110

112

113

115

Taille (en cm)

195

196

196

198

200

201

201

202

205

205

 

Dans des joueurs de rugby  on étudie  la taille et  la masse . Ainsi les deux caractères étudiés sur la population « joueurs de rugby »  sont la masse et la taille .

 

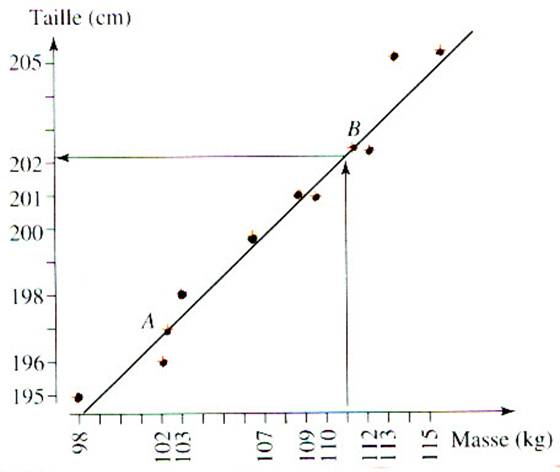
Nuage de points associé.

A chaque individu est associé un couple de valeurs . L’ensemble des couples représentés dans un repère cartésien constitue un « nuage de points »

 

 

DROITE D’ajustement affine 

    L’étude statistique   à deux variables  a pour intérêt de rechercher un lien éventuel entre les deux « caractères » étudiés. 

Il est  possible de mathématiser cette liaison en établissant une loi permettant de prédire  avec un faible degré  d’incertitude  la valeur d’un caractère en fonction de la valeur de l’autre caractère.

L’un des modèles mathématiques les plus simples est la fonction affine dont la représentation graphique  est une droite .

 

Exemple : Dans la représentation précédente  le nuage est séparé en deux parties. Nous déterminons deux points moyens ( A et  B ) se trouvant sur la droite que l’on nomme A et B . Nous pouvons calculer les  coordonnées  des points A et B

Tel que :

Pour le point A :

 

xA   =  = 102,6

 

yA = = 197

 

Pour le point B :

 

XB   =  =111,8

 

YB  =  = 202,8

 

 

Si un joueur remplaçant a une masse  de 111 kg , la lecture  graphique permet d’estimer rapidement sa taille à une valeur également supérieure à 202 cm.

 

Par contre , la lecture graphique ne permet pas d’estimer la taille d’un remplaçant ayant une masse de 95 kg  .

Pour cela , on détermine une équation de la droite  ( AB) :

Y = = 0,63 x + 132,4

Si   la taille d’un remplaçant de masse 95 kg peut être estimée à  192 cm.  

 

TRAVAUX AUTO FORMATIFS.

 

 

CONTROLE :

 

1.       Qu’est qu’une série ?

2.     Donner des exemples de séries ?   que vous connaissez.

 

EVALUATION

 

 

 

 

INTERDISCIPLINARITE

 

 

 

corrigé CONTROLE :

 

Qu’est qu’une série

Donner des exemples de séries ?que vous connaissez.

 

corrigé EVALUATION

 

 

 

 

corrigé INTERDISCIPLINARITE

>