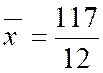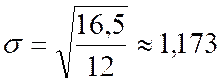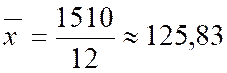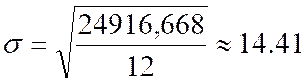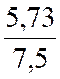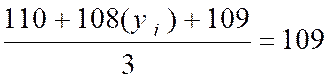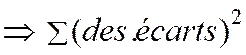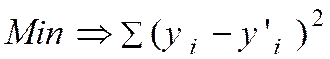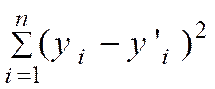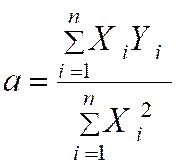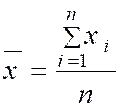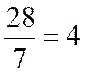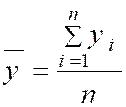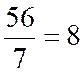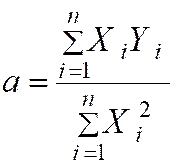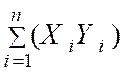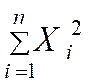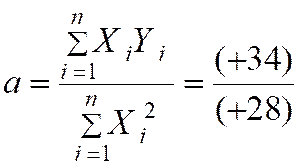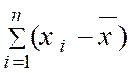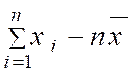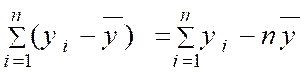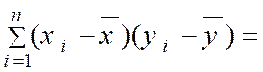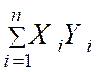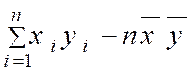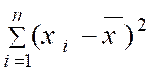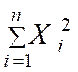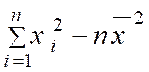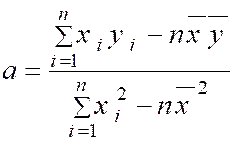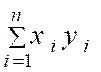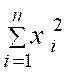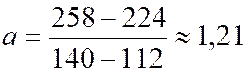COURS

Nous pouvons approfondir notre recherche en essayant de mettre en relation les deux phénomènes. Au lieu de traiter une seule variable (les ventes par exemple), nous analyserons les deux caractères simultanément. Nous sommes en présence de distributions statistiques à deux variables (x_p y).

Nous  avons vu que  l'étude des paramètres de tendance centrale et de dispersion permettent de caractériser une distribution.

 Ainsi, par exemple :

Le nuage de points.

1

Exemple de situation problème n°1 :     y a – t- il une relation de cause à effet entre la vente d’un produit et la publicité que l’on en fait ?

— L'analyse, sur une année, des ventes par correspondantes,  mensuelles (en volume) de  tablettes tactiles   « XC ₃ »  de la société Infotec   a permis d'établir le tableau suivant :

Ventes

Effectifs   «  n _i »

8

1

9

5

10

3

11

2

12

1

12

8 +( 9 x 5) + ( 10 x 3) ( 11 x 2 ) + 12 = 8 + 45 + 30 + 22 + 12 =  117

L’étude , sur une année, des dépenses mensuelles de publicité ( en milliers d’euros) pour les tablettes tactiles « XC ₃ » de la  société Infotec à permis d’établir le tableau suivant.

Dépenses de publicité

Effectifs   «  n _i »

100 

1

110

2

120

3

130

2

140

3

150

1

100 + 220 + 360+ 260+420+150 =  1510

Nous allons analyser ces deux caractères simultanément . Nous allons donc essayer de les mettre en relation .

Dans ce cas nous sommes en présence de « distributions statistiques à deux variables ;  (  x _i ; y _i ) 

Exemple :

Analyse des ventes par mois de la tablette tactile « XC ₃ »   ( y _i )      et des dépenses mensuelles de publicité  (  x _i  )  .

Dépenses de publicité (  x _i  ) 

Ventes correspondantes ( y _i )

100

8

110

9

110

9

120

9

120

9

120

9

130

10

130

10

140

10

140

11

140

11

150

12

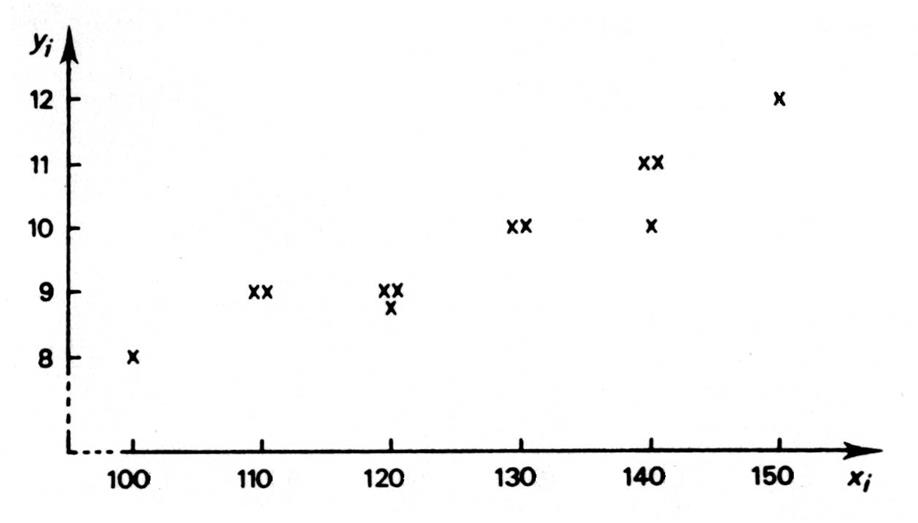
  Lorsque l’on lit le tableau ci-dessus , nous avons « l’intuition » que les deux phénomènes sont dépendants l’un de l’autre .

Cette intuition est renforcée par la construction du graphique sur lequel sont portées , sur l’axe des abscisses , les valeurs   (  x _i  )  et , sur l’axe des ordonnées , les valeurs de ( y _i ).

Ces points constituent un nuage  statistique  .

Expression qui traduit bien le fait qu’il s’agit simplement d’une image faisant apparaître visuellement la « dépendance » des deux caractères .

« lorsque les dépenses de publicité augmentent les ventes progressent »

Ce nuage de points représente  une liaison  parce que les deux variables concernent deux phénomènes .

Exemple de situation problème n°2  : Evolution du chiffre d’affaires de l’entreprise « Y » au cours des dix dernières années.

Années  (  x _i  )

Chiffres d’affaires ( en milliers d’ €) ( y _i ).

1

600

2

710

3

880

4

990

5

1220

6

1300

7

1400

8

1750

9

2100

10

2300

Si l’on représente ces deux variables on obtient aussi un nuage statistique ; celui-ci représente une évolution …( à vous de tracer ce nuage de points)

En résumé :

Un  nuage de point  peut donc représenter :

-          soit une liaison , si les deux variables concernent deux phénomènes . ( cas 1 )

-          Soit  une évolution si l’une des deux variables est le temps.

L’ajustement manuel .

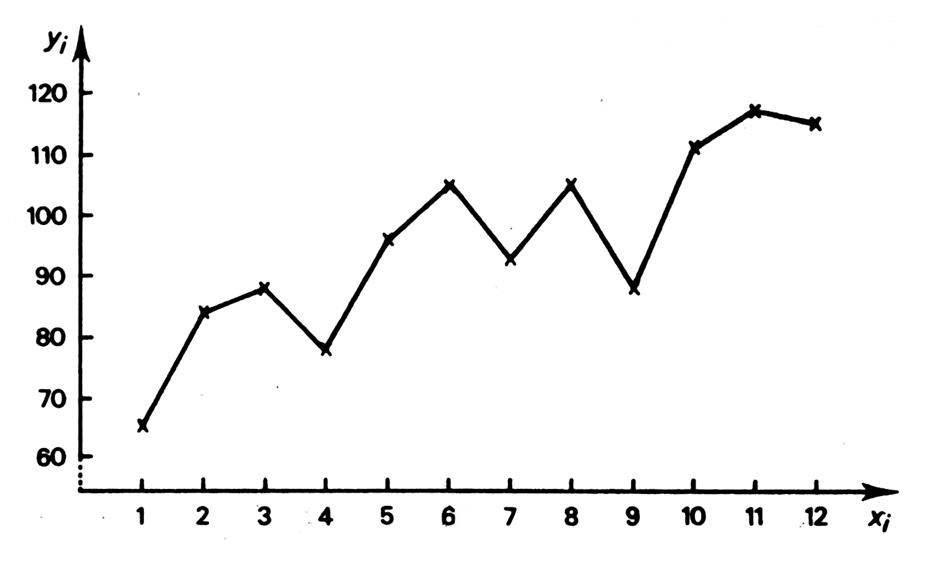
Les ventes d’un produit « P » au cours des douze derniers mois ont été reportées dans le tableau ci contre.

 On reporte ces valeurs  , pour obtenir le graphique ci-dessous : l’ensemble de ces valeurs forment « un nuage » ;

En reliant chaque point au suivant, nous obtenons une courbe irrégulière  ( ligne brisée)

L’ajustement consiste  à éliminer les irrégularités , à déterminer une « courbe régulière » qui va rendre compte de la « tendance générale » et , si possible , à définir la forme algébrique de la relation existant entre ,

(  x _i  )  et  ( y _i )

Période (  x _i  )

Ventes  ( y _i ). ( en unités)

1

66

2

85

3

88

4

78

5

96

6

104

7

92

8

104

9

88

10

110

11

118

12

115

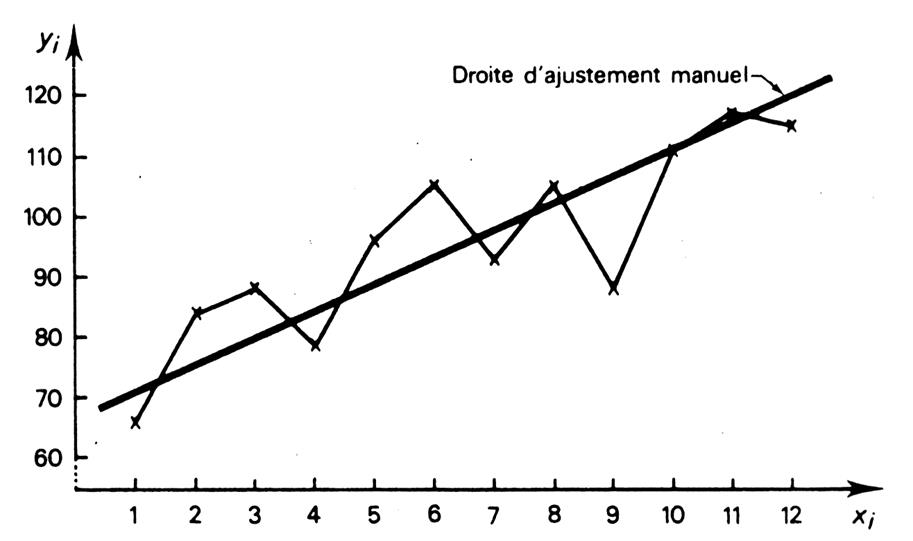
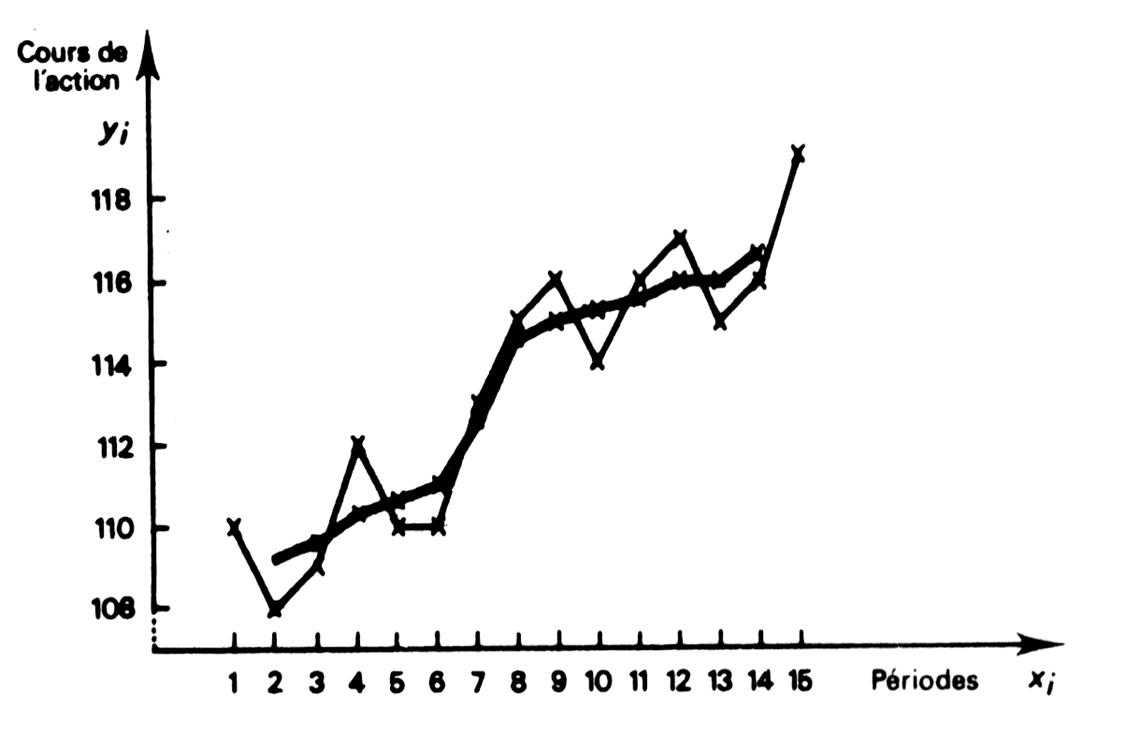
1°) Méthode :

La technique de l’ajustement manuel consiste à tracer , à main levée ou à l’aide d’une règle , une courbe passant au travers du nuage de points , et permettant de compenser , au mieux, les écarts en plus ou en poins .S’il y a peu d’irrégularités , la jonction des points extrêmes de la série donne la tendance.

Voir ci-dessous qui reprend le cas précédent …..

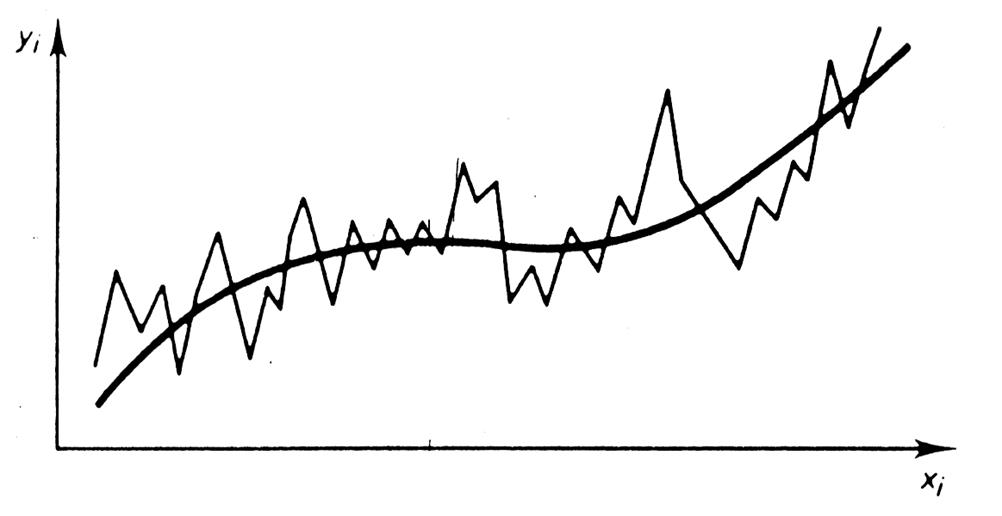
2°) Commentaires :

Bien qu’au premier abord cette méthode paraisse grossière , elle permet néanmoins :

-          de dégager rapidement une tendance générale dans le cas de fluctuations très amples.

-          De faire apparaître simplement une tendance générale dans le cas d’ajustement non linéaire.

Voir ci-dessous l’exemple :

III

L’ajustement par la méthode des moyennes .

Cet ajustement  , appelé aussi « ajustement mécanique » , remplace l’ensemble (  x _i ; y _i ) par de nouveaux ensembles (  x ‘ _n  ; y ‘ _n  ) dont les valeurs sont représentatives ou déduites d’un sous-ensemble de  (  x _i ; y _i ).

Deux méthodes sont possibles . la méthode double moyenne (dit aussi : méthode de Mayer) et la méthode des moyennes mobiles.

1°)  la méthode double moyenne (dit aussi : méthode de Mayer)

Principe :

1°)   Créer deux groupes :

                     Les données sont partagées en deux groupes sensiblement égaux (exactement si le nombre est pair , à une unité prés si le nombre est impair).

2°) Déterminer on détermine les points moyens ( appelés aussi :  barycentres)  « G₁ »  et  «  G ₂ » .

                       Pour chaque groupe , on va déterminer par le calcul ,les coordonnées des deux points moyens . ( ou barycentres)  « G₁ »  et  «  G ₂ » .

3°) Tracer la droite passant par ces deux points : 

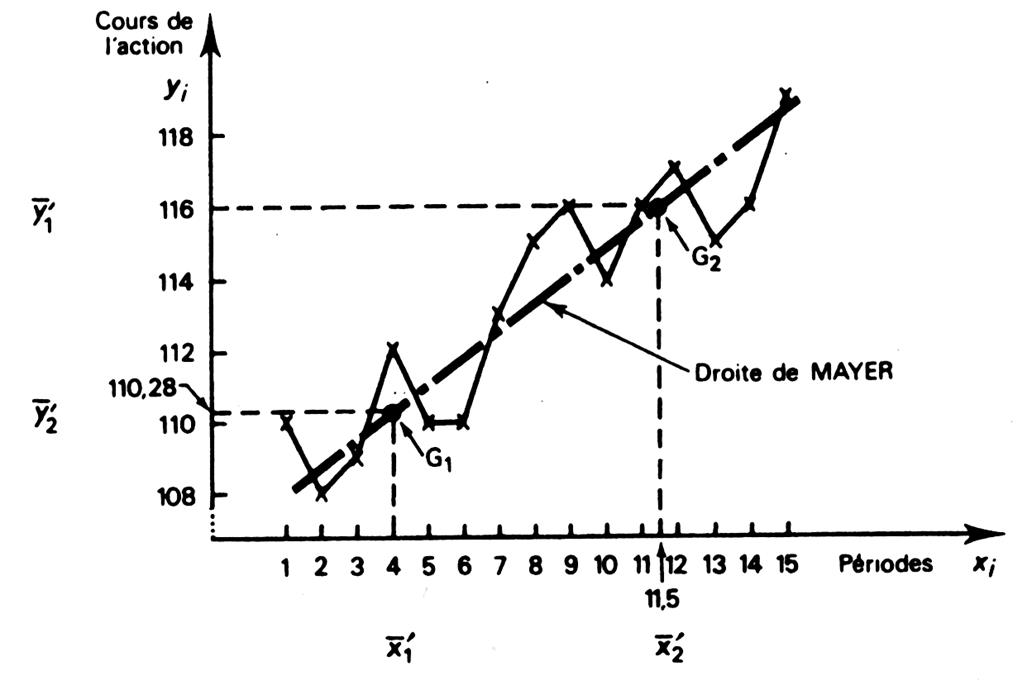
                      La droite ajustée est celle qui passe par ces deux points  « G₁ »  et  «  G ₂ » elle est appelée :« droite de Mayer »

Exemple de situation problème :

On relève les valeurs d’une action ( cours de la bourse) pendant une durée décomposée en 15 périodes.

Période

(  x _i  )

Cours de l’action :

(  y _i )

1

110

Pour  G1 :

2

108

Pour : G1 :

(  x ‘ ₁  ) =  ( 1 + 2 + 3 + 4 + 5 + 6 + 7 ) / 7

3

109

(  y’ ₁ ) = ( 110 + 108+109+112+110+110+113) /7

(  x ‘  ₁  ) =  28 / 7 .

4

4

112

110,29

(  y’ ₁ ) = 110,29

(  x ‘ ₁  )=  28 / 7  =   4

5

110

6

110

G 1

7

113

G2

8

115

Pour  G2 :

9

116

Pour : G2 :

 ( x ₂  ) =  ( 8 + 9 + 10+11+12+13+14+15 )/ 8

10

114

(  y ₂ ) = ( 115+116+114+116+117+115+116+119) / 8

( x ₂  ) =  92 / 8

1  1,5

11

116

1 1 6

(  y ₂ ) = ( 928 ) / 8

( x ₂  ) =  1  1,5

12

117

(  y ₂ ) =   1 1 6

13

115

14

116

15

119

Pour obtenir les coordonnées du point G 1   (  x ‘ ₁ ;  y’ ₁ )

Pour obtenir les coordonnées du point G 2   (  x ‘ ₂ ;  y’ ₂ )

-          Pour   x ‘ ₁  =    ( moyenne arithmétique )

-          Pour   x ‘ ₂  =    ( moyenne arithmétique )

-          Pour   y ‘ ₁  =    ( moyenne arithmétique )

-          Pour   y ‘ ₂  =    ( moyenne arithmétique )

G ₁  ( 4 ; 110,29)

G ₂ ( 11,5 ; 116)

Info ++

Détermination de l’équation de la droite de Mayer :

Comme nous l’avons vu précédemment ; la courbe d’ajustement  est une droite passant par deux point, c’est non plus une ligne brisée comme dans le cas vu ci-dessus .

Puisque nous connaissons les coordonnées de deux point d’une droite , il est alors possible ( et facile) de déterminer l’équation de la droite ( de la forme y = a . x + b )

Reprise de l’exemple précédent :

-          Les coordonnées du point « G ₁  ( 4 ; 110,29) » doivent vérifier l’équation :          110 , 29  =   a .  4     +  b       

-          Les coordonnées du point « G ₂  ( 11,5  ; 116) » doivent vérifier l’équation :                1 1 6  =   a .  11,5   + b      

On va résoudre le système de deux équations (par soustraction)

Des deux équations nous obtenons : 

7,5 a = 5 , 73

a = 

a =  0, 764

d’où « b »  =  110,29  - 4 ( 0,764)

« b » =  110 , 29 -  3, 056

« b » =  +  107, 234

Conclusion N°1 : l’équation de la droite de Mater est :     y =  0,764 x  + 107 , 234

Conclusion N°2 : l’intérêt de cette méthode est de permettre le calcul de paramètres de la droite d’ajustement , ce qui rend possible  les prévisions.

Suite de l’ exemple : Si la tendance se maintient, quel sera le cours de l’action pour la prochaine période  ( la n°16)

En termes mathématiques , cette question peut se traduire de la façon suivante :

« Quelle sera la valeur de « y » ( cours de l’action) si « x = 16 » ? »

 «  y = 0, 764 x 16 + 107,234 »  

«  y = 0, 764 x 16 + 107,234 »  

«  y = 119,468  »  

Cette valeur ,ainsi calculée, est appelée « valeur théorique » . Il sera intéressant de la comparer, à la période suivante, à la « valeur observée » (valeur réelle)

Cette méthode , évidemment simple, à l’inconvénient d’être très approximative, surtout quand le nombre de points composant le nuage est élevé et que leurs valeurs sont très disparates.

a

3-2 méthode des moyennes mobiles.  ( principe,application, commentaires)

Procédure .

Pour « écrêter » et « lisser » les irrégularités  que présente une série (à deux variables) , une autre méthode est possible.

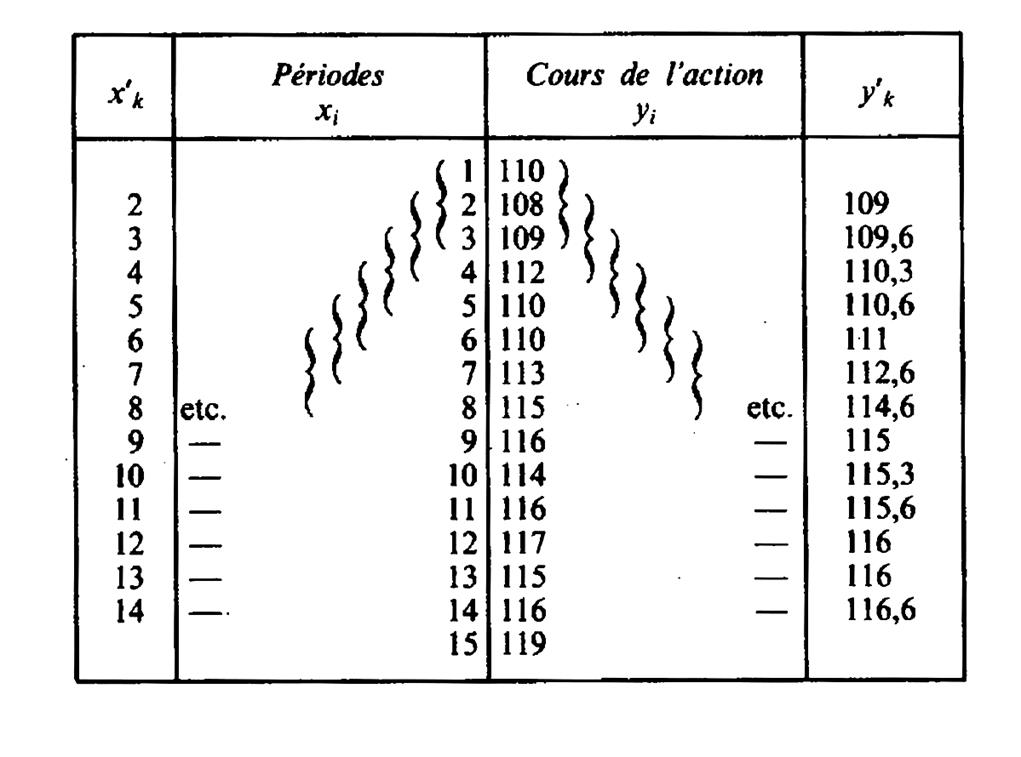
Elle consiste à remplacer une valeur « y _i » , par la moyenne «  y ‘_N » de cette observation et des « 2 n » observations qui l’entourent, et de poursuivre le travail en reprenant toujours «  n – 1 » éléments de la moyenne précédente.

Dans l’exemple suivant  ( reprise des valeurs de l’exemple précédent ) nous fixons «  n – 1 »

Notre première moyenne «  y ‘_N » se détermine de la façon suivante :

Après les calculs , les couples de nombres , vont permettre de construire une « courbe » :

( 2 ; 109) ; ( 3 ; 109,6) ; (4 ; 110,3 ) ; ………..

Commentaires :

Ce procédé permet :

-          de conserver, par rapport à la méthode précédente, un plus grand nombre de points moyens, ce qui explique son utilisation courante ;

-          d’éliminer les variations saisonnières.

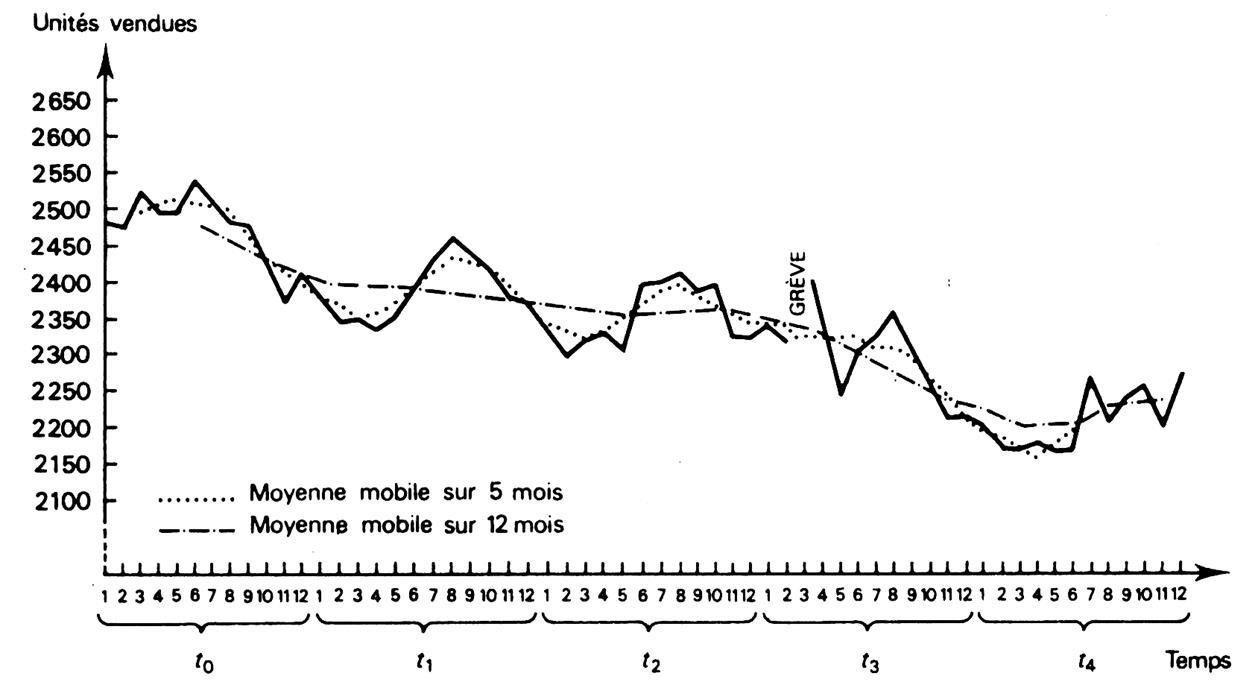
L’INSEE , dans ses tableaux de « tendances et conjonctures »,recourt le plus souvent à des moyennes mobiles de « 3 » ( indiqué MM3) ou 12 mois ( MM12)

Dans l’exemple qui suit , deux moyennes mobiles ont été calculées, l’une sur 5 mois , l’autre sur 12 mois. Cette dernière donne la tendance générale du nombre

Ci-dessous : l’évolution des ventes de la clé USB 2   ( 4 go) :

Remarque :  En regroupant plusieurs années ( « 36 mois » par exemple) ,une tendance à long terme , ou trend , peut apparaître.

Ce procédé possède un inconvénient :

Cet inconvénient réside dans le fait que la courbe ainsi ajustée se trouve amputée à ses extrémités  de quelques éléments (entres autres :  t ₀  1 ; et  t ₄ 12 ) . Ceci est d’autant plus grave que bien souvent ces ajustements ont pour but de permettre des prévisions à court terme.

4

L’ajustement linéaire par la méthode des moindres carrés. (principe , les paramètres « a » et « b » de la  droite des moindres carrés,  procédés de calcul ; représentation graphique de la droite dit « droite de régression de « y » en « x »  » , intérêt de ce calcul)

1°) Méthode et principe.

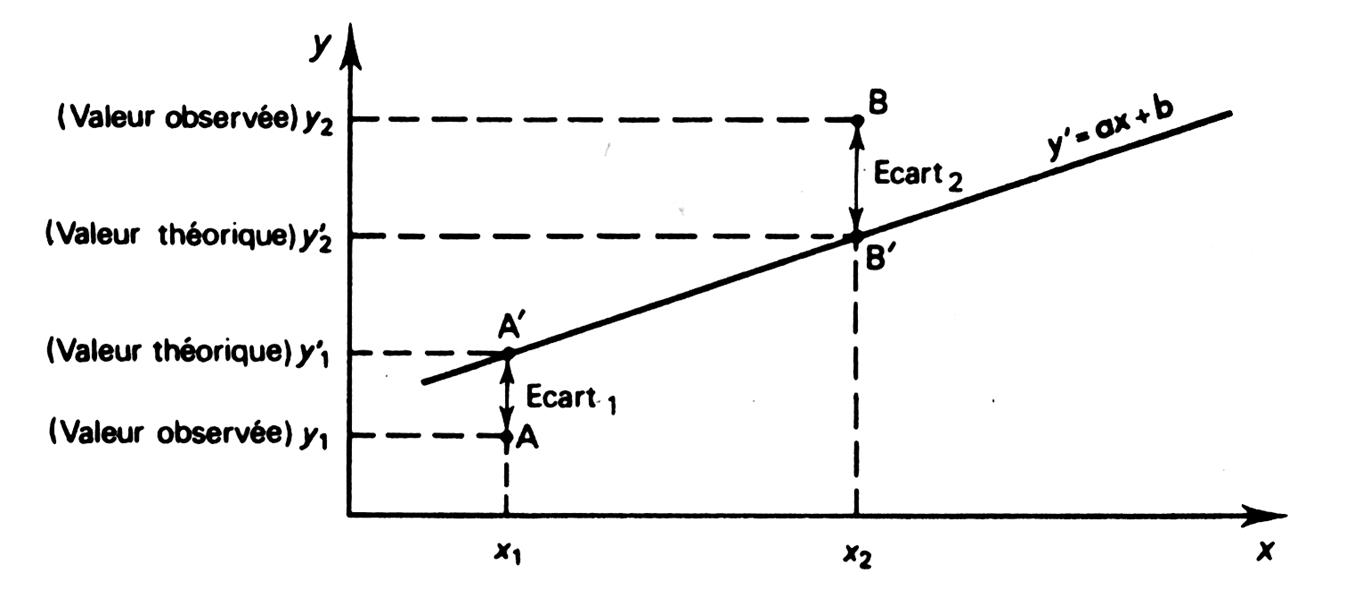
La méthode est basée sur le principe qu’il faut réduire « au maximum » les écarts verticaux entre les valeurs observées et les valeurs théoriques fournies par la droite d’ajustement.

Le but étant de minimiser les écarts :   ( Ecart ₁  + Ecart ₂ + …….+ Ecart _n ) que nous écrivons : Min

L’écart se définit comme mesurant algébriquement la différence entre la valeur observée et la valeur ajustée.

«  écart ₁  = y ₁ – y ’ ₁ »

«  écart ₂  = y ₂ – y ’ ₂ »

Cette différence peut être positive «  écart ₂  = y ₂ – y ’ ₂ » , négative  «  écart ₁  = y ₁ – y ’ ₁ » , ou nulle ( si les valeurs théoriques et observée sont confondues) .

Pour éliminer ce problème de signe et faire en sorte que la sommation de ces écarts ne se traduise pas par une compensation quand ils sont de signes contraires on les élèves au  carré , ce qui les rend tous positifs.

Nous cherchons donc à : Min

L’expression d’un écart quelconque peut s’écrire «  écart _i  = y _i – y ’ _i » ; donc la droite la plus représentative est celle pour laquelle la somme des carrés des écarts est minimale, d’où le nom de «  méthode des moindres  carrés » 

2°)   Détermination des paramètres « a »  et « b » de la droite des moindres carrés

En développant cette expression et  en remplaçant « y ’ » par sa valeur  en fonction de « x _i » , on arrive  à  un trinôme du second degré qui sera minimum lorsque sa dérivée sera nulle.

On arrive ainsi à définir le coefficient angulaire « a » et le paramètre « b » de la droite des moindres carrés. Dit « droite de régression »

i

Avec :

X _i = x ₁ -

Y _i  = y ₁  -

 Et avec   :     «  b  =     - a  »

Il faut noter que la droite passe  par le point caractéristique  qui est le point  moyen de coordonnées  (   ; )

3°) Exemple type  de l’étude d’une situation problème ( cliquez ici pour avoir plus d’informations sur l conduite de la résolution.

Semaines : x _i

Ventes de tablettes

Tactiles ( par milliers) : y _i

1

6

2

4

3

6

4

8

5

10

6

10

7

12

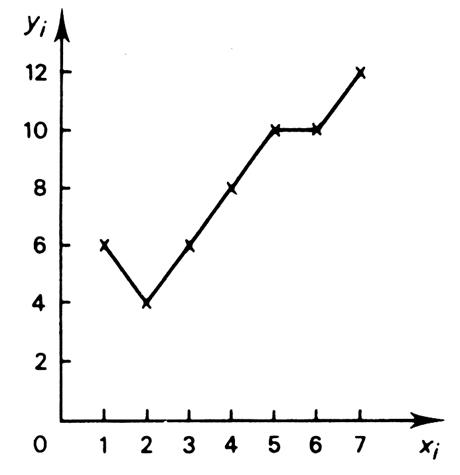
Le nuage de points , sur le graphique ci-dessus , laisse penser que l’on peut ajuster une droite à cette série.

Pour obtenir cet ajustement , nous allons calculer son équation par la méthode des moindres carrés.

Procédure à mettre en œuvre  pour effectuer cet ajustement. (ordre chronologique en 6 étapes)

1°étape ) Détermination des coordonnées du point moyen :  (   ; )

a)     Calcul de «  » :    =

b)     Calcul de «  » :    =

2° étape ) Détermination des valeurs des écarts  pour les   X _i  et  les  Y _i 

A partir de mesures « données précédemment  et reportées dans le tableau (1) et (2) » on doit calculer les valeurs des écarts  ( 3) et ( 4 )

Sachant que «  = 4  » «  = 8»

Colonne ( 1)

Colonne ( 2 )

Colonne ( 3 )

Colonne ( 4 )

Colonne ( 5 )

x _i

y _i

X _i  =  ( x _i - )

Soit le calcul  =   ( x _i – 4 )

Y _i  = ( y _i - )

Soit le calcul   =  ( y _i – 8 )

1

6

( 1 – 4 ) =  ( - 3 )

( 6 – 8 ) = ( - 2 )

2

4

( 2 – 4 ) = ( - 2 )

( 4 – 8 ) = ( - 4  )

3

6

( 3 – 4 ) = ( - 1 )

( 6 – 8 ) = ( - 2 )

4

8

( 4 – 4 ) = (  0 )

( 8 – 8 ) = ( 0 )

5

10

( 5  – 4 ) = ( +1  )

( 10 – 8 ) = ( + 2 )

6

10

( 6  – 4 ) = ( + 2 )

( 10  – 8 ) = ( + 2 )

7

12

( 7  – 4 ) = ( + 3  )

( 12  – 8 ) = ( + 4  )

3°) Troisième étape : Détermination du coefficient « a » de la droite de régression.       Sachant que : 

(Attention de respecter les règles des signes du produit de deux nombres relatifs)  

A)  Faire  le calcul des produits : ( X _i  par  Y _i )  et calculer la somme    ( le numérateur de l’expression de «a »  )  : 

Colonne ( 1)

Colonne ( 2 )

Colonne ( 3 )

Colonne ( 4 )

Colonne ( 5  )

Colonne ( 6)

x _i

y _i

X _i 

Y _i

( X _i .Y _i )

1

6

  ( - 3 )

 ( - 2 )

( - 3 ) ( - 2 )=  ( + 6 )

2

4

( - 2 )

( - 4  )

( - 2 ) ( - 4  ) = ( + 8 )

3

6

( - 1 )

 ( - 2 )

( - 1 ) ( - 2 )= ( + 2 )

4

8

(  0 )

( 0 )

(  0 ) ( 0 ) = 0

5

10

( +1  )

( + 2 )

( +1  ) ( + 2 ) =  ( + 2 )

6

10

( + 2 )

( + 2 )

( + 2 ) ( + 2 )= ( + 4 )

7

12

 ( + 3  )

( + 4  )

( + 3  ) ( + 4  ) = ( + 12 )

  = 

( +34 )

B)  Elever au carré les valeurs  «X _i » et en calculer la somme :  ( le dénominateur  de l’expression de «a »  )  :

Colonne ( 1)

Colonne ( 2 )

Colonne ( 3 )

Colonne ( 4 )

Colonne ( 5  )

Colonne ( 6)

x _i

y _i

X _i 

Y _i

( X _i .Y _i )

X _i ²

1

6

  ( - 3 )

 ( - 2 )

( + 6 )

( - 3 ) ( - 3 )=    ( + 9 )

2

4

( - 2 )

( - 4  )

( + 8 )

( - 2 ) ( - 2 )=    ( + 4 )

3

6

( - 1 )

 ( - 2 )

( + 2 )

( - 1 ) ( - 1 )=    ( + 1)

4

8

(  0 )

( 0 )

0

( 0 ) ( 0 )= (        0 )

5

10

( +1  )

( + 2 )

( + 2 )

( +1  ) ( +1  )=    ( +1  )

6

10

( + 2 )

( + 2 )

( + 4 )

( + 2 ) ( + 2 )=   ( + 4 )

7

12

 ( + 3  )

( + 4  )

( + 12 )

( + 3  ) ( + 3  )= ( + 9 )

 =( +34 )

=  ( + 28 )            

C ) Nous pouvons calculer  la valeur de « a » :

34 / 28    1,2142857142857142857142857142857

à   0,01 prés :

a   =  1 , 21

4°) Quatrième  étape : Calcul de « b »

Nous connaissons «  = 4  » «  = 8» et « a  = 1,21 » , le calcul de « b » devient simple :

On sait que   =  a    + b    , par transformation de l’égalité : b =   -  a    

En remplaçant par les valeurs connues :  b =  8  - (  1,21 x 4 ) ;    b = 8 – 4,84                                                               

D’où

b = + 3,16

5 °) Cinquième  étape : Reste à définir la forme générale de l’équation de la droite de regression.

                 L’équation étant de la forme «  y = a x + b » ; puisque « a = 1,21 » et «  b = + 3,16 »

                                                                                               Alors l’équation est égale à :   «  y = 1,21 x + 3,16 »

Fin des calculs…

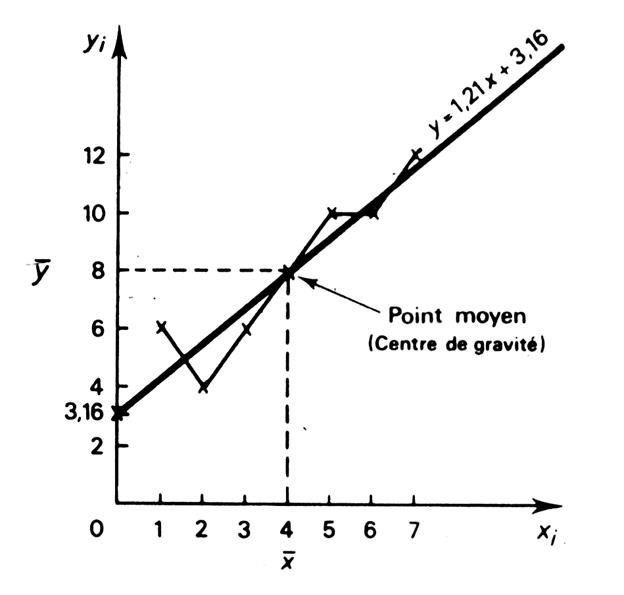
Représentation graphique de la droite. «  y = 1,21 x + 3,16 »

Nous savons que la droite passe par le point moyen ( 4 ; 8 ) .

Et quand «  x = 0 »   on constate que « y = 3,16 »

Exemple  d’utilisation de ces calculs précédents .

Connaissant l’équation de la droite « de tendance » , il est aisé de prévoir les ventes de la 8^ème semaine , et par la même de passer une commande correspondante.

Nous posons donc « x = 8 » et nous calculons la valeur théorique de « y » :

«  y = ( 1,21 x 8 + 3,16 )       ; on trouve        y  13

 Etablissement d’une formule permettant de calculer « a »  adaptée à l’utilisation d’une calculatrice…

Le calcul des expressions « Xi » et « Yi » est longue et fastidieux, surtout si la série statistique est longue. En effet , il nécessite deux soustractions ( x _i - ) et ( y _i - )  pour chaque couple de valeurs. On peut transformer cette formule     en une formule mieux adaptée à l’utilisation de l calculatrice scientifique .

On démontre en effet que :

  =

  = 

=    = 

On peut donc écrire :   ;………….( attention aux signes….)

Cette formule n’exige de saisir chaque valeur  « x _i »  et   «  y _i » qu’une seule fois.

Si nous reprenons l’exemple précédent :  calculons terme à termes , remplaçons ensuite dans la formule…….

Colonne ( 1)

Colonne ( 2 )

Colonne ( 3 )

Colonne ( 4 )

Colonne ( 5  )

Colonne ( 6)

x _i

y _i

1

6

6 + 8+ 18+32+50+60+84=

7 x 4x 8 =

1+4+9+16+25+36+49 =

7 x  4² =

2

4

3

6

4

8

=  258

= 224

= 140

= 112

5

10

6

10

7

12

    ;      = d’ où