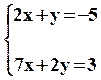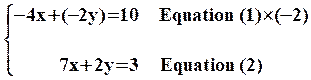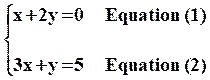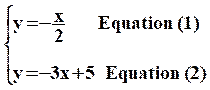|
|
Résumé
du cours sur la résolution d’un système d’équations
|
|
|
|
|
|
|
|
Dans
ce cours est présenté trois méthodes de résolution d'un système de deux d'équations
à deux inconnues.
En
général on note x et y les inconnues.
Un
système d'équation sert à résoudre des problèmes du premier degré dans
lesquels deux solutions sont à déterminer.
Résoudre
le système d'équation d'inconnues x et y suivant : 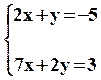 (par exemple) (par exemple)
consiste
à trouver les valeurs de x et y qui soient solutions des deux équations du système en même temps. La
solution du système est notée ( valeur de x ; valeur
de y )
Il
existe (entre autres) trois méthodes de résolution :
¬ Méthode
dite de "substitution"
Méthode
dite de "combinaison"
® Méthode
dite "graphique"
|
|
Par la METHODE DE SUBSTITUTION
Reprenons
l'exemple précédent :
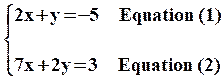
Cette
méthode consiste à exprimer à l'aide de l'équation(1) y en fonction de x et de
remplacer y par son expression en fonction de x dans l'équation(2). On ramène
ainsi l'équation (2) à une équation du premier degré d'inconnue x que l'on peut
résoudre.
¬ Transformation
de l'équation(1) :
2x + y =
-5 ñ y = - 5 - 2x Equation(1)
Remplacement
de l'équation(1) dans l'équation(2) et résolution de l'équation (2)
7x + 2 (-5 - 2x ) = 3
7x -10 - 4x =
3
3x - 10 = 3
donc 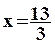
® Remplacement
de la valeur de x trouvée dans l'Equation(1) transformée
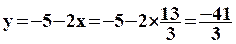
¯ Vérification
de la solution
La
solution du système est : 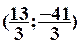
Vérification
pour l'équation (1)
: 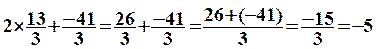
L'équation
(1) est vérifiée pour 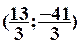
Vérification
pour l'équation (2)
: 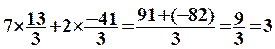
L'équation(2)
est vérifiée pour 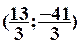
La
solution du système 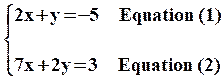 est :
est : 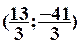
Par la METHODE DE COMBINAISON
Cette
méthode consiste à multiplier les équations par des nombres choisis de manière
à ce que les coefficients d'une inconnue soient opposés, puis on additionne
membre à membre les deux équations obtenues. On obtient ainsi une équation du
premier degré à une inconnue que l'on résout pour trouver la valeur d'une
inconnue.
Avec
le système choisis au départ : 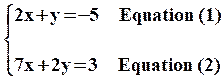
On
choisit de déterminer x , on veut éliminer y en
additionnant membre à membre les deux équations pour cela on multiplie
l'équation (1) par (-2)
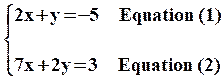 í
í 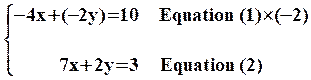
On
additionne les deux équations précédentes membre à membre, puis on résout
l'équation en x :
-4x + (-2y) +
7x + 2y = 10 + 3
3x = 13
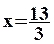
Pour
déterminer la valeur de y on remplace x par 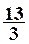 dans une des deux équations.
dans une des deux équations.
Par
exemple l'équation (1) : 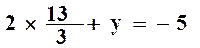 donc :
donc : 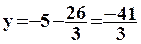 La solution de ce système est donc :
La solution de ce système est donc : 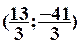
On
considère dans cette méthode les deux équations comme deux équations de
droites.
Soit
le système : 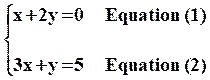
On
écrit ensuite les deux équation de ce système sous la forme plus classique
d'une équation de droite ( de la forme y = ax + b )
Ce
système devient : 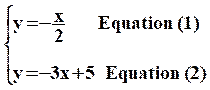
On
trace ensuite ces deux droites dans un repère convenablement choisi :
La
droite d'équation (1) passe par les points de coordonnées (0 ; 0 ) et (4 ; -2 )
La
droite d'équation (2) passe par les points de coordonnées (0 ; 5 ) et ( 3 ; -4 )
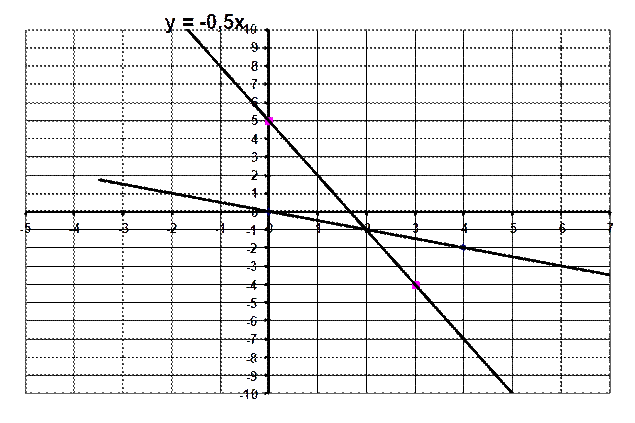 Les
coordonnées du point d'intersection des 2 droites donne ainsi la solution du
système d'équation soit
Les
coordonnées du point d'intersection des 2 droites donne ainsi la solution du
système d'équation soit
(2
; -1 )
Vérification : Equation (1) : 2 +
2´(-1)
= 2 -2 = 0
Equation (2) : 3´2 + (-1) = 6 -
1 = 5
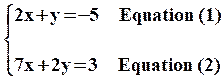
![]()
![]()