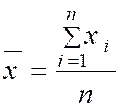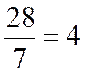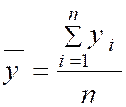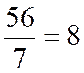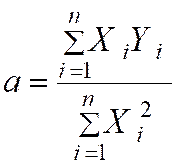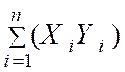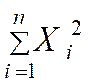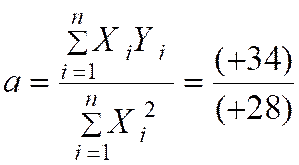Situation problème N°1  :

Soit les données ci-dessous ; Calculer l’équation de la droite de régression.

Les données sont : 

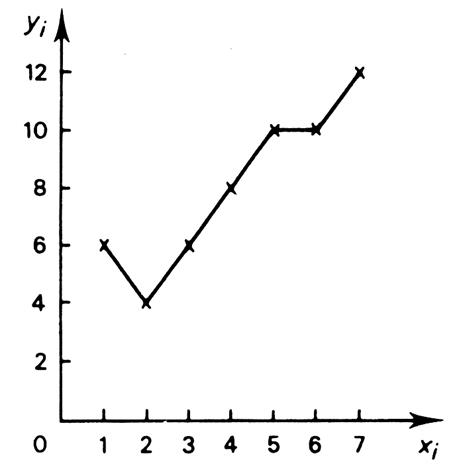
Ci-dessous après avoir construit le nuage de point , on a relié chaque point pour obtenir le graphique ci-dessous….

Semaines : x _i

Ventes de tablettes

Tactiles ( par milliers) : y _i

1

6

2

4

3

6

4

8

5

10

6

10

7

12

Le nuage de points , sur le graphique ci-dessus , laisse penser que l’on peut ajuster une droite à cette série.

Pour obtenir cet ajustement , nous allons calculer son équation par la méthode des moindres carrés.

Résolution : Procédure à mettre en œuvre  pour effectuer cet ajustement. (ordre chronologique en 7 étapes)

1°étape ) Détermination des coordonnées du point moyen :  (   ; )

a)     Calcul de «  » :    =

b)     Calcul de «  » :    =

2° étape ) Détermination des valeurs des écarts  pour les   X _i  et  les  Y _i 

A partir de mesures « données précédemment  et reportées dans le tableau (1) et (2) » on doit calculer les valeurs des écarts  ( 3) et ( 4 )

Sachant que «  = 4  » «  = 8»

Colonne ( 1)

Colonne ( 2 )

Colonne ( 3 )

Colonne ( 4 )

Colonne ( 5 )

x _i

y _i

X _i  =  ( x _i - )

Soit le calcul  =   ( x _i – 4 )

Y _i  = ( y _i - )

Soit le calcul   =  ( y _i – 8 )

1

6

( 1 – 4 ) =  ( - 3 )

( 6 – 8 ) = ( - 2 )

2

4

( 2 – 4 ) = ( - 2 )

( 4 – 8 ) = ( - 4  )

3

6

( 3 – 4 ) = ( - 1 )

( 6 – 8 ) = ( - 2 )

4

8

( 4 – 4 ) = (  0 )

( 8 – 8 ) = ( 0 )

5

10

( 5  – 4 ) = ( +1  )

( 10 – 8 ) = ( + 2 )

6

10

( 6  – 4 ) = ( + 2 )

( 10  – 8 ) = ( + 2 )

7

12

( 7  – 4 ) = ( + 3  )

( 12  – 8 ) = ( + 4  )

3°) Troisième étape : Détermination du coefficient « a » de la droite de régression.       Sachant que : 

(Attention de respecter les règles des signes du produit de deux nombres relatifs)  

A)  Faire  le calcul des produits : ( X _i  par  Y _i )  et calculer la somme    ( le numérateur de l’expression de «a »  )  : 

Colonne ( 1)

Colonne ( 2 )

Colonne ( 3 )

Colonne ( 4 )

Colonne ( 5  )

Colonne ( 6)

x _i

y _i

X _i 

Y _i

( X _i .Y _i )

1

6

  ( - 3 )

 ( - 2 )

( - 3 ) ( - 2 )=  ( + 6 )

2

4

( - 2 )

( - 4  )

( - 2 ) ( - 4  ) = ( + 8 )

3

6

( - 1 )

 ( - 2 )

( - 1 ) ( - 2 )= ( + 2 )

4

8

(  0 )

( 0 )

(  0 ) ( 0 ) = 0

5

10

( +1  )

( + 2 )

( +1  ) ( + 2 ) =  ( + 2 )

6

10

( + 2 )

( + 2 )

( + 2 ) ( + 2 )= ( + 4 )

7

12

 ( + 3  )

( + 4  )

( + 3  ) ( + 4  ) = ( + 12 )

  = 

( +34 )

B)  Elever au carré les valeurs  «X _i » et en calculer la somme :  ( le dénominateur  de l’expression de «a »  )  :

Colonne ( 1)

Colonne ( 2 )

Colonne ( 3 )

Colonne ( 4 )

Colonne ( 5  )

Colonne ( 6)

x _i

y _i

X _i 

Y _i

( X _i .Y _i )

X _i ²

1

6

  ( - 3 )

 ( - 2 )

( + 6 )

( - 3 ) ( - 3 )=    ( + 9 )

2

4

( - 2 )

( - 4  )

( + 8 )

( - 2 ) ( - 2 )=    ( + 4 )

3

6

( - 1 )

 ( - 2 )

( + 2 )

( - 1 ) ( - 1 )=    ( + 1)

4

8

(  0 )

( 0 )

0

( 0 ) ( 0 )= (        0 )

5

10

( +1  )

( + 2 )

( + 2 )

( +1  ) ( +1  )=    ( +1  )

6

10

( + 2 )

( + 2 )

( + 4 )

( + 2 ) ( + 2 )=   ( + 4 )

7

12

 ( + 3  )

( + 4  )

( + 12 )

( + 3  ) ( + 3  )= ( + 9 )

 =( +34 )

=  ( + 28 )            

C ) Nous pouvons calculer  la valeur de « a » :

34 / 28    1,2142857142857142857142857142857

à   0,01 prés :

a   =  1 , 21

4°) Quatrième  étape : Calcul de « b »

Nous connaissons «  = 4  » «  = 8» et « a  = 1,21 » , le calcul de « b » devient simple :

On sait que   =  a    + b    , par transformation de l’égalité : b =   -  a    

En remplaçant par les valeurs connues :  b =  8  - (  1,21 x 4 ) ;    b = 8 – 4,84                                                               

D’où

b = + 3,16

5 °) Cinquième  étape : Reste à définir la forme générale de l’équation de la droite de regression.

                 L’équation étant de la forme «  y = a x + b » ; puisque « a = 1,21 » et «  b = + 3,16 »

                                                                                               Alors l’équation est égale à :   «  y = 1,21 x + 3,16 »

Fin des calculs…

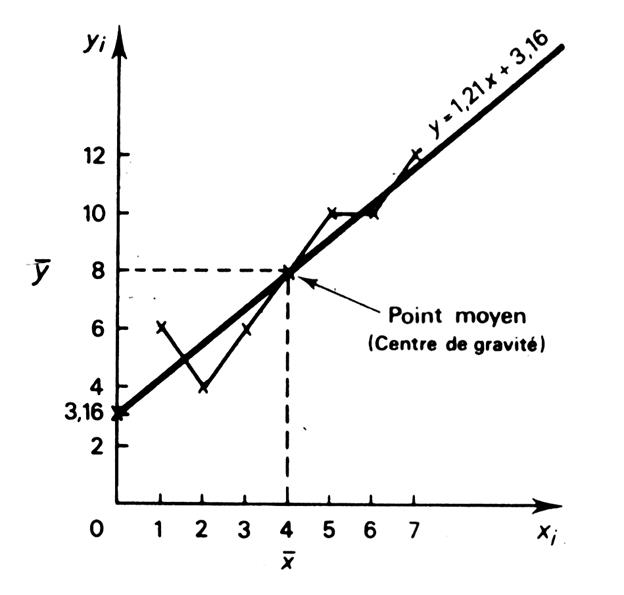
6°) Représentation graphique de la droite. «  y = 1,21 x + 3,16 »

Nous savons que la droite passe par le point moyen ( 4 ; 8 ) .

Et quand «  x = 0 »   on constate que « y = 3,16 »

7°)   Exemple  d’utilisation de ces calculs précédents .

Connaissant l’équation de la droite « de tendance » , il est aisé de prévoir les ventes de la 8^ème semaine , et par la même de passer une commande correspondante.

Nous posons donc « x = 8 » et nous calculons la valeur théorique de « y » :

«  y = ( 1,21 x 8 + 3,16 )       ; on trouve        y  13

Autres sujets : (difficulté croissante : A , B , C , D )

Situation problème N° 2 : (A)

x _i

3

5

7

8

10

11

y _i

16

14

14

9

7

5

1° ) Construire le nuage de points associés à cette série

2°) Calculer les coordonnées du point moyen du nuage.

Situation problème N° 3 : (A)

Année de naissance ( x _i )

1965

1970

1975

1980

1985

1990

1995

Espérance de vie ( y _i )

67,5

68,4

69,0

70,2

71,3

72,7

73,9

Source INSEE . 1997

1°) Déterminer l’équation de la droite des moindres carrés.

2°) Quelle espérance de vie peut-on prévoir pour un homme né en 2 000 ?

Situation problème N° 4 :  d’après un sujet BAC ES 1997.   (A)

D’après un carnet de santé, on peut lire le poids moyen d’un enfant de sa naissance à 12 ans .

Age ( en années)

( x _i )

0

1

2

4

7

11

12

Masse ( en kg)

( y _i )

3,4

7

10,5

14,5

20,5

33

37,5

Aucun calcul manuel n’est demandé…

Dans cet exercice les résultats seront donnés à 10 ^-1 prés .

Le plan est rapporté à un repère orthogonal ( unités graphiques : 0,5 cm pour une année en abscisse , 0,5 cm pour 2 kg en ordonnées)

1°)

a : Représenter le nuage de points associé à la série statistique ( x _i ; y _i ) .

b :Déterminer et représenter le point moyen de cette série.

2°)

a : Donner une équation de la droite de régression  « D  »  de « y » en « x ».

b :Représenter  « D  »   sur le graphique précédent.

3°)

a : Déterminer graphiquement, en expliquant le raisonnement utilisé, à partir de quel âge le poids moyen d’un enfant dépasse 25 kg.

b :Retrouver ce résultat par le calcul en utilisant l’équation de la droite « D  ».

Situation problème N° 5 :  (A)