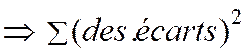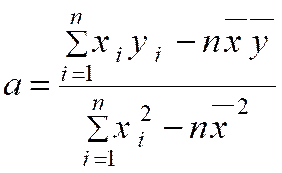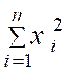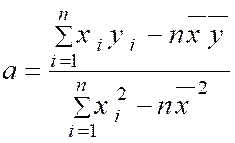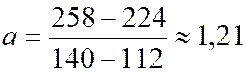COURS

Au lieu de traiter une seule variable (les ventes par exemple), nous analyserons les deux caractères simultanément. Nous sommes en présence de distributions statistiques à deux variables (x_p y).

Précédemment : Nous  avons vu que  l'étude des paramètres de tendance centrale et de dispersion permettent de caractériser une distribution.

1

Le nuage de points.

Nous allons analyser ces deux caractères simultanément . Nous allons donc essayer de les mettre en relation .

Dans ce cas nous sommes en présence de « distributions statistiques à deux variables ;  (  x _i ; y _i ) 

Exemple :

Analyse des ventes par mois de la tablette tactile « XC ₃ »   ( y _i )      et des dépenses mensuelles de publicité  (  x _i  )  .

Dépenses de publicité (  x _i  ) 

Ventes correspondantes ( y _i )

100

8

110

9

110

9

120

9

120

9

120

9

130

10

130

10

140

10

140

11

140

11

150

12

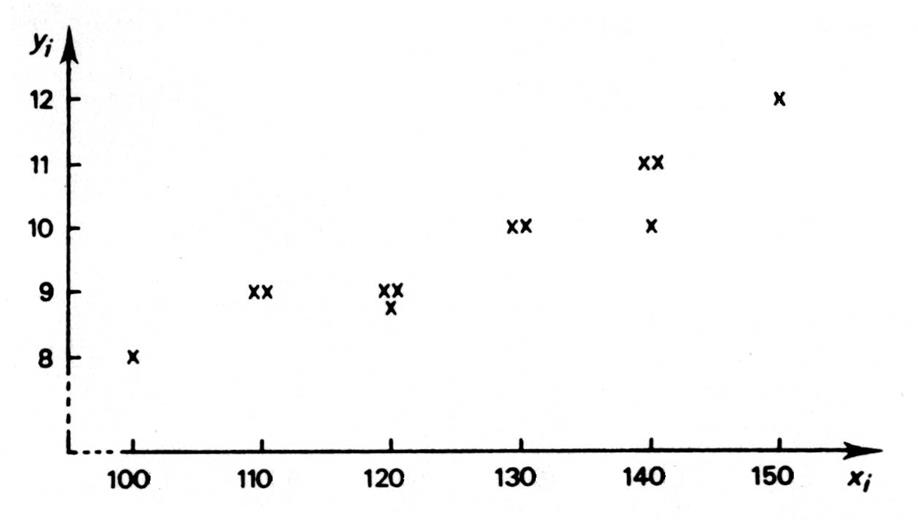
  Lorsque l’on lit le tableau ci-dessus , nous avons « l’intuition » que les deux phénomènes sont dépendants l’un de l’autre .

Cette intuition est renforcée par la construction du graphique sur lequel sont portées , sur l’axe des abscisses , les valeurs   (  x _i  )  et , sur l’axe des ordonnées , les valeurs de ( y _i ).

Ces points constituent un nuage  statistique  .

Expression qui traduit bien le fait qu’il s’agit simplement d’une image faisant apparaître visuellement la « dépendance » des deux caractères .

« lorsque les dépenses de publicité augmentent les ventes progressent »

Ce nuage de points représente  une liaison  parce que les deux variables concernent deux phénomènes .

Exemple de situation problème n°2  : Evolution du chiffre d’affaires de l’entreprise « Y » au cours des dix dernières années.

Années  (  x _i  )

Chiffres d’affaires ( en milliers d’ €) ( y _i ).

1

600

2

710

3

880

4

990

5

1220

6

1300

7

1400

8

1750

9

2100

10

2300

Si l’on représente ces deux variables on obtient aussi un nuage statistique ; celui-ci représente une évolution …( à vous de tracer ce nuage de points)

Calcul de   :

 ( 1 +2+3+4+5+6+7+8+9+10)  /  10 

=   55 / 5 

= 5,5

Calcul de  :=   ( 600+710+880+990+1220+1300+1400+1750+2100+2300) / 10

=  13250 / 10

=  1325

Remarque :     et   sont les coordonnées du « point moyen » ,. Point  par lequel passe  le droite de régression…….

Un  nuage de point   représente :

-          soit une liaison , si les deux variables concernent deux phénomènes .

-          Soit  une évolution si l’une des deux variables est le temps.

Résumé : On retiendra :

·      Une série statistique à deux variables ( dit aussi : série statistique double ») est  un ensemble des (  x _i ; y _i ) avec () , résultats de l’étude de deux caractères quantitatifs pour chacun des « n » individus d’une population. 

·      Lorsqu’on représente une série statistique double (  x _i ; y _i ) avec () ,, dans un repère orthogonal, par les points de coordonnées (  x _i ; y _i ) , on obtient un nuage de points.

·      Le point moyen du nuage est le point dont les coordonnées sont ( ; ) moyennes respectives des (  x _i ; y _i )

2

L’ajustement affine  ( dit aussi : linéaire) par la méthode des moindres carrés.

1°) Méthode et principe.

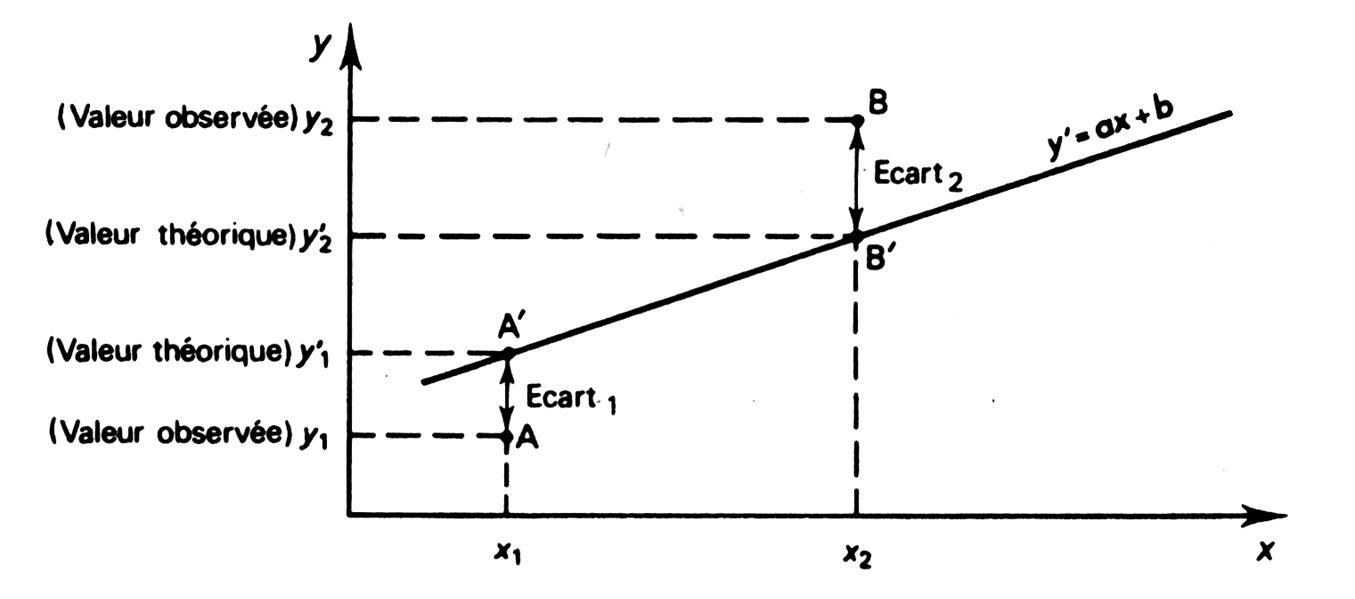
La méthode est basée sur le principe qu’il faut réduire « au maximum » les écarts verticaux entre les valeurs observées et les valeurs théoriques fournies par la droite d’ajustement.

Le but étant de minimiser les écarts :   ( Ecart ₁  + Ecart ₂ + …….+ Ecart _n ) que nous écrivons : Min

L’écart se définit comme mesurant algébriquement la différence entre la valeur observée et la valeur ajustée.

«  écart ₁  = y ₁ – y ’ ₁ »

«  écart ₂  = y ₂ – y ’ ₂ »

Cette différence peut être positive «  écart ₂  = y ₂ – y ’ ₂ » , négative  «  écart ₁  = y ₁ – y ’ ₁ » , ou nulle ( si les valeurs théoriques et observée sont confondues) .

Pour éliminer ce problème de signe et faire en sorte que la sommation de ces écarts ne se traduise pas par une compensation quand ils sont de signes contraires on les élèves au  carré , ce qui les rend tous positifs.

Nous cherchons donc à : Min

L’expression d’un écart quelconque peut s’écrire «  écart _i  = y _i – y ’ _i » ; donc la droite la plus représentative est celle pour laquelle la somme des carrés des écarts est minimale, d’où le nom de «  méthode des moindres  carrés ». 

2°)  Autrement dit : ajustement affine par moindre carrés

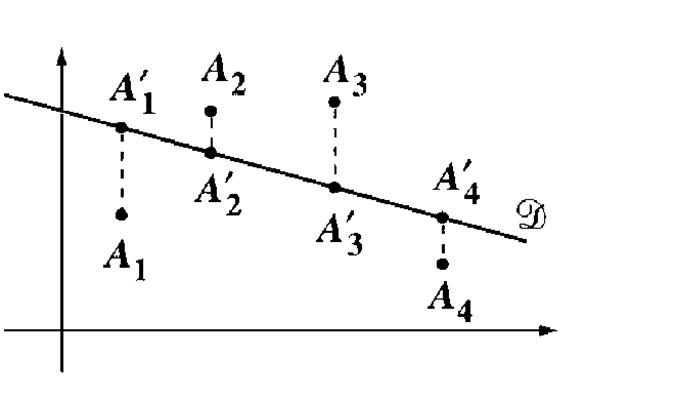
    Un nuage de points « n »  ,  ou  A₁ ( x₁ ; y ₁) ;  A₂ ( x₂ ; y ₂) ; …….. A_n ( x_n ; y _n)  et une droite  ( D )  d’équation «  y =  a x + b » étant donnés , on peut calculer la somme des carrés des distances «  A _i A ‘ _i » , où « A ‘ _i » est le projeté de   «  A _i  » sur ( D  ), parallèlement à l’axe des ordonnées.

La droite qui minimise la somme des carrés des distances «  A _i A ‘ _i » est appelée « droite de régression de « y » en « x » ou plus simplement « droite des moindres carrés. »

Cette droite passe par le point moyen du nuage et son coefficient directeur est :

Cette droite à pour équation : 

  y -    =  a ( x -  ) 

A partir de l’équation de la droite des moindre carrés , on peut estimer « y » pour une valeur donnée « x »  ou « x » pour une valeur de « y » donnée.

Exemple de calcul manuel  :  calculons terme à termes , remplaçons ensuite dans la formule…….

Colonne ( 1)

Colonne ( 2 )

Colonne ( 3 )

Colonne ( 4 )

Colonne ( 5  )

Colonne ( 6)

x _i

y _i

1

6

6 + 8+ 18+32+50+60+84=

7 x 4x 8 =

1+4+9+16+25+36+49 =

7 x  4² =

2

4

3

6

4

8

=  258

= 224

= 140

= 112

5

10

6

10

7

12

    ;      = d’ où        

Ajustement se ramenant à un ajustement affine.

Dans le cas où le nuage de points d’une série statistique double n’a pas une forme allongée à laquelle une droite pourrait s’ ajuster, il peut être intéressant  d’effectuer une transformation sur une des deux variables pour examiner si le nuage de la nouvelle série double obtenue est formé de point se répartissant mieux selon une ligne droite.

Une fois trouvée la relation entre les variables de la série transformée , on revient aux variables de la série initiale en utilisant la transformation réciproque .

Ainsi , si une série (  x _i ; y _i ) est transformée en posant «  t _i = ln (  y _i ), on obtient une équation de droite des moindres carrés de la forme «  t = a x + b » et on revient à une équation entre « x » et « y » en remplaçant « t » par « ln y », ce qui conduit à :

ln y  =  a x + b

Puis    «  y = e ^ax+b »

Ou     «  y =  e ^ax x e ^b »

Soit , en posant  « e ^b = B  »,………………..             «  y = B e ^ax  »

Fin du résumé.

Voir la résolution d’exercices et situations types.