|
DOC : formation individualisée soutien en ligne. |
DOC : livre
Elève .Cours interactifs - et
travaux + corrigés. |
DOSSIER
(1/5) : LES EGALITES Nomenclature 1
|
DOSSIER N°4-A : INTERACTIF |
Information
« TRAVAUX » |
|
OBJECTIFS : - Savoir
définir ; identifier et reconnaître : un terme , un facteur , un facteur commun |
I ) Pré requis:
|
-
Lecture : les conventions
d’écriture en algèbre : coefficient ; lettres ;…. |
|
|
|
II ) ENVIRONNEMENT du dossier :
|
|
|
|
Classe
de collège : 6ème |
|
Objectif précédent : 3°) L’égalité et l’inégalité ,et
double inégalité en classe de 6ème
|
Objectif suivant : |
|
III )
LECON n° 4-A :
DOSSIER (1/5) : L ‘
égalité ; l’inégalité ; la double inégalité. Terminologie ;
Nomenclature-
Vocabulaire
Chapitres :
|
I ) L’EGALITE .( signe ; vocabulaire, propriétés) |
|
|
II ) Les
INEGALITES. |
|
|
III ) DOUBLE INEGALITE. |
|
|
IV ) ORDRE DE
GRANDEUR D’UN ENTIER NATUREL , ENCADREMENT . |
|
|
V)
MULTIPLICATION OU DIVISION PAR 10 ; 100 ; 1 000 |
|
|
|
|
|
|
|
IV) INFORMATIONS « formation leçon » :
|
|
|
Corrigé des travaux
auto - formation. |
|||||
|
|
|||||||
V ) DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
|
|
|
|
|
Devoir
Formatif « Contrôle :
savoir » ; ( remédiation) |
|
|
|
|
|
Devoir sommatif . |
|
|
Devoir certificatif : ( remédiation ) |
|
* remédiation : ces documents peuvent être réutilisés
( tout ou partie) pour conclure une formation .
|
|
|
|
|
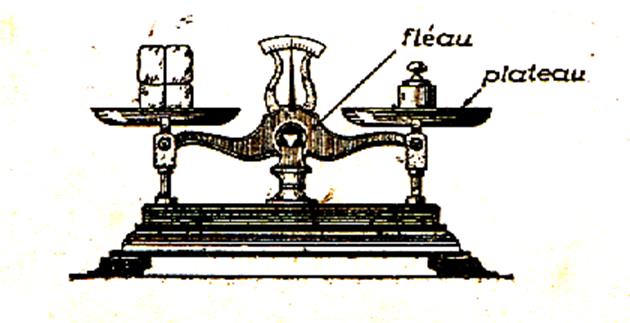
L’appareil utilisé pour faire
penser à l’égalité est
la balance Roberval. (ci
contre) (cette balance est un instrument de mesure par comparaison) L’aiguille est à zéro ; Les plateaux sont équilibrés. La balance est en équilibre lorsque « Ce qu ‘il a sur le plateau
de droite est égal à ce qu’il y a sur la plateau de gauche. » |
|
|
|
|
|
|
Le signe : |
|
|
|
« 13 + 7 =
5 x 4 »
s’appelle une égalité. |
|
|
|
Elle exprime que ce qui est de part et d’autre du signe
« = » est de la même valeur. En effet : on calcule « 13 + 7 » ,
on trouve « 20 » ; puis on calcule « 5
x 4 » , on trouve
« 20 » On dira que « 13 + 7 =
5 x 4 » est « une phrase mathématique » ; et cette phrase
est « vraie ». |
|
|
|
On retiendra : Une égalité est une phrase mathématique qui se présente
sous la forme « a = b » ou
« A = B » dans laquelle « A » et « B »
représente le même objet
mathématique |
|
|
|
Remarques :
· Quand
on écrit « A = B » ,on sous entend que cette phrase est
« vraie ». · Si
la phrase « A = B » n’est pas vraie , on
écrit : « A · «
A |
|
|
|
Vocabulaire : Dans toutes les égalités : -
ce qui s’écrit à gauche du signe
« = »égal s’appelle « le membre de gauche » ou
« premier membre » -
ce qui s’écrit à droite du signe égal « = »s’appelle
« le membre de droite » ou « deuxième membre » |
|
|
|
Propriété
1 : « a » et « b » représente le même nombre , On peut écrire indifféremment les égalités « a = b » ou
« b = a » |
|
|
|
Propriété
2 : « a » , « b » et
« c » désignant des nombres ; Si « a = b » et
« b = c », alors
« a » , « b » et « c »
représentent le même nombre ; on peut dons écrire « a = c ». Quand « a = b »
et « b = c » ;
on écrit parfois , par convention, « a = b = c » |
|
|
|
|
|
|
|
Exercice : Dans un devoir , un élève a
écrit « 8 x 5 = 40 +7 =
47 » Expliquer (oralement ) pourquoi c’est faux et
donner une bonne écriture. |
|
|
|
|
|
|
|
Le signe de reconnaissance de l’égalité
est le symbole : « = » Ce qui est incontestable : ce qu’il y a « à droite » du
signe est égale à ce qu’il y a « à gauche » du signe égal . En
sciences : l’égalité est
représentée (symbolisé) par la balance de Roberval .
Après l’, équilibrage des plateaux ( les
plateaux sont horizontaux , l’aiguille réglée au « zéro ») la
balance Roberval est l’image type de l’égalité dans un partage. On
dit que , ce
qu’il y a sur le plateau de gauche est égal en masse à ce qu’il y a sur le
plateau de droite. Construction de ce symbole de l’égalité : le symbole de l’égalité est le
tracé de deux traits forts ,parallèles ,et parallèle a la ligne d’écriture,
d’environ 3 mm de longueur. C’est le signe le plus utilisé ! Quand
ce n’est pas égal : on dit « inégal » le symbole est :¹ ; c’est
ensuite que l’on peut effectuer un
classement , en ordre. ! ! !, alors que l’ on a pas trouvé l’égalité . Attention : les expressions algébriques sont des simplifications ( écriture simplifiée ) des sommes algébriques ; il
est donc impératif de savoir transformer les expressions algébriques en somme
algébrique avant de rechercher à
identifier , les termes . |
|
|
|
Les INEGALITES. |
||||||
|
|
Nous avons déjà rencontré des « inégalités » à l’école
élémentaire ; par exemple : 3 <
7 ( qu’il
faut lire : 3 est inférieur à
7) ; on dit aussi : « 3 est plus petit que 7 » ou 9 > 4 ( qu’il faut
lire : 9 est supérieur à 4 )
; on dit aussi : « 9
est plus petit que 4 » En voici d’autres : |
||||||
|
|
on
lit : le nombre « x » est inférieur ou égal à 9 |
on
lit : le nombre « y » est supérieur ou égal à 3 |
|
||||
|
|
Ce sont des phrases mathématiques , dont le
verbe est représenté par un des quatre signes : :
< ; > ; |
|
|||||
|
|
On retiendra : |
|
|||||
|
|
« a » et
« b » représentent des nombres |
|
|||||
|
|
|
La phrase mathématique : |
Se lit en écriture littérale |
|
|
||
|
|
|
« a > b » |
« a » est strictement supérieur à « b » |
|
|
||
|
|
« a <
b » |
« a » est strictement inférieur à « b » |
|
||||
|
|
« a |
« a » est supérieur ou égal à « b » et signifie : « a > b »
ou « a =
b » |
|
||||
|
|
« a |
« a » est inférieur ou égal à « b » et
signifie : « a
< b »
ou « a =
b » |
|
||||
|
|
|
|
|||||
|
|
Remarque 1 :
« x » et « y » représente des nombres ; « x
> y » a la même signification que
« y < x » |
|
|||||
|
|
Remarque 2 : Comme pour
les égalités, dans toute égalité, on parle de : « membre de gauche » et « membre de droite ; ou de
« premier membre » et « deuxième membre ». |
|
|||||
|
|
|
|
|||||
|
|
Exercice : Compléter en utilisant convenablement >
ou < . |
|
|||||
|
|
|
|
|||||
|
|
14 ……………7 ; 27 ……………………34 ; 126 …………18 ; 248
………………. 5462 |
|
|||||
|
|
|
|
|||||
|
|
Vocabulaire :
|
|
|||||
|
|
-
9
> 5 et 13 > 7 sont des
inégalités de même sens . -
Il
en est de même pour 5 < 7 et 8 < 11
ou ou x
-
9
> 5 et 5 < 7 sont des inégalités de sens contraire. |
|
|||||
|
|
Exercices : Ecrire des
inégalités de même sens : ………………………………………………………………………………. Ecrire des inégalités de sens
contraire : …………………………………………………………………………… |
|
|||||
|
|
DOUBLE INEGALITE. |
||||
|
|
|
|
|||
|
|
Considérons les deux inégalités de même sens : 7
< 13 et 13
< 39 |
|
|||
|
|
Dans la suite naturelle des nombres entiers naturels, « 7 »
est placé avant « 13 » , et « 13 » est placé avant
« 39 »., on a donc
« 7 » est placé avant « 39 » On condense ces 3 inégalités par une double inégalité : 7
< 13 <
39 ; les nombres
« 7 ; 13 ; 39 »
sont alors rangés dans l’ordre croissant. · On
peut faire de même avec plusieurs inégalités de même sens : 7 < 13 ; 13 <
39 ; 39 < 67 , on écrit
alors : 7 < 13
< 39 < 67 · On
peut faire de même avec les : > ; |
|
|||
|
|
Attention :
Dans le cas 4 < 13
et 13 > 11
, on ne peut pas écrire
4 < 13 > 11 par ce que les nombres ne sont ni
rangés par ordre croissant ni dans l’ordre décroissant. |
|
|||
|
|
Exercice : on vous donne des phrases mathématiques
, barrer celles qui sont fausses ou incorrectes : |
|
|||
|
|
33
> 15 < 17 |
15 |
27
< 54 > 16 |
27 |
|
|
11 |
43 |
16
< 13 < 19 |
23
< 47 < 47 |
||
|
|
|
|
|||
|
|
Exercice 1 : |
|
|||
|
|
En utilisant le signe < ;
ranger dans l’ordre croissant les nombres suivants : 13 ; 43 ; 8 ; 132 ; 27 ;55 ;2 ;
139 ……………………………………………………………………………………………………………………………………………………………………………………. |
|
|||
|
|
Exercice 2 : Ranger dans l’ordre décroissant les nombres
suivants en utilisant le symbole convenable.: 15 ; 43 ; 9 ; 133 ; 27 ;65 ;
2 ; 169 ………………………………………………………………………………………………………………………………………………………………………………………. |
|
|||
|
|
IV )
ORDRE DE GRANDEUR D’UN ENTIER NATUREL , ENCADREMENT . |
|
|
|
a ) On sait que 325 846 est voisin de 300
000 ; que 7247 est voisin de 7000. On dit que 325 846 est de l’ordre des centaines de mille ;
que 21 675 est de l’ordre des dizaine de mille et que
7247 est de l’ordre des mille. On dit que 300 000 est un ordre
de grandeur de 325 846 , que 20 000 est un ordre de grandeur de 21 675 et que 7000 est un ordre de grandeur de 7436 Dans le cas de 48 873 , on peut prendre 50
000 comme ordre de grandeur ; ( 48
étant plus prés de 50 que de 40 ) Un ordre de grandeur est aussi
appelé « arrondi ». b) l’encadrement : ( double inégalités) ( INFO PLUS +++) suivant l’ordre choisi ou imposé on
peut encadrer « 325 846 » : 300 000 < 325 846 < 400 000 ; si
l’on veut être plus précis , on peut
« resserrer » l’encadrement . comme 320 000 < 325 846
< 330 000 ; ou comme 325 000 < 325 846
< 326 000 c) « valeur approchée par excès » ou « valeur approchée
par défaut » prenons par exemple : 300 000 < 325 846
< 400 000 ; nous dirons : 300 000 est la valeur approchée à 100 000 près par défaut de 325 846. 400 000 est la valeur approchée à 100 000 près par excès de 325 486 . Au lieu de dire « valeur approchée » on dit aussi «
approximation » Autres
exemples : 320 000 < 325 846 < 330 000 ; les valeurs approchées sont à
10 000 près. 325 000 < 325 846 <
326 000 ; les valeurs approchées sont à 1 000 près. Les valeurs approchées peuvent être de plus en plus précises : |
|
|
Avec 7437 |
Avec 48 738 |
|
7 000 < 7437 < 8 000 7 400 < 7437 < 7 500 7 430 < 7437 < 7 440 7 436 < 7437 < 7 438 |
40 000 < 48 738 < 50 000 48 000 < 48 738 < 49 000 48 700 < 48 738 < 48 800 48 730 < 48 738 < 48 740 48 737 < 48 738 < 48 739 |
|
|
V) MULTIPLICATION OU DIVISION PAR 10 ;
100 ; 1 000 d’un nombre entier |
|
||||||
|
|
|
|
|
|
|
|||
|
|
|
|
||||||
|
|
« Multiplier » |
|
||||||
|
|
|
|
||||||
|
|
· Pour
multiplier un nombre entier par « 10 » , il faut placer un
zéro à la droite de ce nombre. |
|
||||||
|
|
Exemples : 35 x 10
= 350 ; 9300 x 10 = 93000 |
|
||||||
|
|
· Pour
multiplier un nombre entier par « 100 » , il faut placer deux zéros à
la droite de ce nombre. |
|
||||||
|
|
Exemples : 35 x 100
= 3500 ; 9300 x 100 = 930000 |
|
||||||
|
|
· Pour
multiplier un nombre entier par « 1
000 » , il faut placer trois zéros à la droite de ce nombre. |
|
||||||
|
|
Exemples : 35 x 1000
= 35000 ; 9300 x 1000 = 9300000 |
|
||||||
|
|
Compléter : 57 x
10 000 = ……………………………… ;
831 x 100 000= …………………………… |
|
||||||
|
|
|
|
||||||
|
|
« Diviser » |
|
||||||
|
|
· Pour
diviser par « 10 ;100 ;
1 000 ; … » on enlève un ou des zéros ; ( si le nombre se termine par un ou des
zéros) |
|
||||||
|
|
54 000 :
10 = 5400 ;
500 / 100 = 5 ;
47000 : 1000 = 47 |
|
||||||
|
|
· Pour
diviser par « 10 ;100 ;
1 000 ; … » on décale une virgule vers la gauche ; ( si le nombre ne se termine pas par un ou des zéros) |
|
||||||
|
|
54 :
10 = 5, 4 ;
1 55 : 100 = 1 ,55
; 4700 : 1000 =
4,7 ; 93 : 100 = 0,93 ; 93,7 : 100 = 0,937 , |
|
||||||
|
|
|
|
||||||
|
|
Cas avec des nombres décimaux : ( nombres « à virgule ») |
|
||||||
|
|
|
|
||||||
|
|
« MULTIPLIER » |
|
||||||
|
|
|
|
||||||
|
|
· Multiplier
par « 10 » : pour multiplier un nombre décimal par
« 10 » on décale la virgule de 1 rang vers la droite. |
|
||||||
|
|
3,2 x 10 = 32 |
24,5 x 10 = 245 |
2,34 x 10 = 23,4 |
543,567x 10 = 5435 , 67 |
|
|||
|
1,02 x 10 = 10,2 |
0,35 x 10 = 3,5 |
|
|
|||||
|
|
· Multiplier
par « 100 » : pour multiplier un nombre décimal par
« 100 » on décale la virgule de 2 rangs vers la droite. |
|
||||||
|
|
3,45 x 100
= 345 |
368,956 x 100 =
36895,6 |
0,456 x 100 = 45,6 |
0,056x 100 = 5,6 |
|
|||
|
|
|
|
|
|||||
|
|
·
Multiplier par « 1000 » : pour
multiplier un nombre décimal par « 1000 » on décale la virgule de 3
rangs vers la droite. |
|
||||||
|
|
368,956 x 1000 = 368
956 |
0,015 x 1000 =
15 |
0,5678x 1000= 567,8 |
|
|
|||
|
|
|
|
||||||
|
|
« DIVISER » |
|
||||||
|
|
·
Pour diviser un
nombre décimal par « 10 » on décale la virgule de 1 rang vers la gauche . |
|
||||||
|
|
24,5 : 10
= 2,45 |
2,34 : 10
= 0, 234 |
|
|
|
|||
|
|
·
Pour diviser un
nombre décimal par « 100 » on décale la virgule de 2 rangs vers la gauche . |
|
||||||
|
|
|
|
|
|
|
|||
|
|
·
Pour diviser un
nombre décimal par « 1000 » on décale la virgule de 3 rangs vers la
gauche . |
|
||||||
|
|
|
|
|
|
|
|||
|
|
Exercice 1 |
|
||
|
|
Compléter en utilisant 10 ou
100 ou 1000 ou 10 000 ou ….. |
|
||
|
|
5,76
x …..= 57,6 |
1,57
x …………= 15 700 |
0,0043
x …………………= 0,43 |
|
|
273 : …………= 0,273 …… |
0,082 :
…………………….= 0,00082 |
9,7 :
………………= 0,97 |
||
|
|
|
|
||
|
|
Faire comme précédemment mais en précisant l’opération : « : » ou « x » |
|
||
|
|
52,18 …………………………………….= 0,5218 |
0,17………………………………..= 170 |
34 ……………………………………..= 0,0034 |
|
|
63,17……………………………………..= 0,006 317 |
43,7 ………………………………….= 437 000 |
84,532………………………………….= 84 532 |
||
|
0,073………………………………………= 730 |
0,0052……………………………….= 0,00052 |
54 381 …………………………………..= 543,81 |
||
|
|
|
|
||
|
|
Exercice 2 : compléter les égalités. |
|
||
|
|
……………………x 1 000 = 18 |
………………………………x 10 000= 7,2 |
…………………………………….x 10 = 647,8 |
|
|
……………………… : 1 000 = 0,8354 |
…………………………………….. : 100= 84,75 |
……………………………………… : 10 = 0,057 |
||
|
|
Faire comme précédemment : |
|
||
|
|
…………………………………. : 10 000=0,0065 |
…………………….x 100 = 3459 |
…………………………………… : 100 = 7,325 |
|
|
………………………………x 1 000 = 23 000 |
………………………. :
1 0 000= 0,42 |
………………………………… : 100 = 13,6 |
||
|
………………………………… : 1 000= 437 |
………………………. :
1000 = 0,0000093 |
……………………………………x 10 = 0,038 |
||
|
|
|
|
||
|
|
Ce qui termine ce cours de 6ème
|
|
||