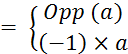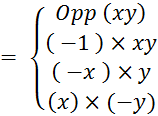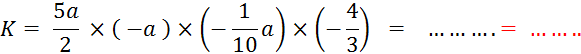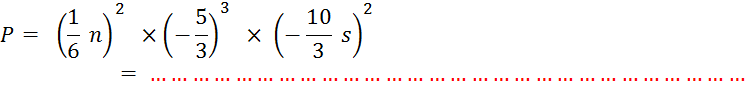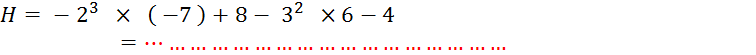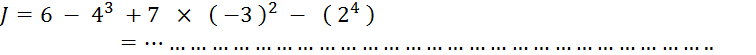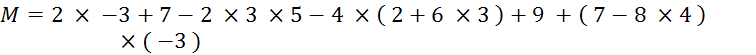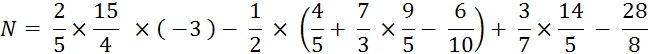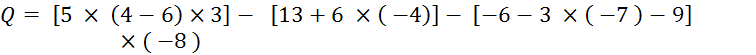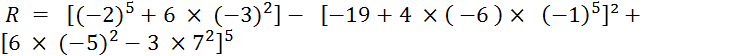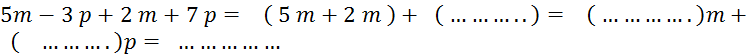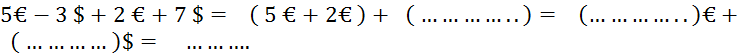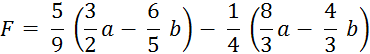Voir le cours sur le produit de n ombres relatifs.

Fiche 1 : Différentes significations de « -a »

Rappel :

« a » désignant un nombre relatif quelconque, vous avez vu dans la  « leçon …… »que le produit d’un nombre par (-1) est égal à ………………………de ce nombre.

Or, vous savez (vu dans la leçon …..) que « Opp(a) »  s’écrit « -a ». On dira alors :

A retenir :

«  » étant un nombre relatif quelconque,  et   sont deux nombres égaux que l’on écrit «  »

Dans un calcul où figure «  »,  vous choisissez l’interprétation de «  » qui convient :

1° cas : vous voulez simplifier l’ écriture de 

«  » est alors considéré comme  ………………….de «  ».

 Il peut se simplifier avec «  » ( au même titre que «  » et «  »). On a alors   : 

2° cas : vous voulez simplifier l’ écriture de 

« -a » est alors considéré comme le produit de par «  ».

On a alors   c’est   à dire :    

Fiche 2 : Différentes significations de « »

« x » et « y » désignant des nombres relatifs,

·       D’ après une leçon .info @  . ;    ou  

·       Transformons l’écriture  de    

·       Transformons l’écriture  de   

A retenir :

«  » étant un nombre relatif quelconque,  et  ;     sont deux nombres égaux que l’on écrit «  »

Cas particulier :

Transformons

Fiche 3 : Récapitulation des conventions d’écritures

«  » et «  » désignant des nombres relatifs quelconques, complétez le tableau donnant l’écriture simplifiée de la somme ou du produit de deux nombres.

Nombres

Sommes

Produit

Fiche 4 : Simplification de l’écriture d’un produit.

Principe général :

Dans un produit , toutes les fois que c’est possible , on supprime  le signe

Nombres  écrits en chiffres :

  peut s’écrire      ou      ou    ou  

Mais ne peut s’écrire :       ce serait une …………………… .

Ni écrire :     car on ne doit pas écrire  2 signes consécutifs,

Ni écrire    :   car on confondrait  avec le nombre   

·       Nombres écrits en lettres :  

« «  s’écrit toujours «  »

On a coutume d’écrire les lettres dans l’ordre alphabétique : 

·       Cas des parenthèses :

Une parenthèse peut être assimilée à une lettre.

 s’écrit      ;   et      s’écrit     

·       Des chiffres et des lettres  ( ou parenthèses)

  s’écrit 

Mais ne s’écrit pas       ( le nombre écrit en chiffres se place toujours devant )

Comme il de s’écrit pas     ( on confondrait avec une  ………………..) 

  s’écrit     mais ne s’écrit pas     ( on confondrait avec une …………………….)

Convention :

Si entre des nombres écrits en chiffres ou des lettres ou des parenthèses , il n’y a pas de signe , l’opération est une …………………………………..

L’écriture d’un produit se simplifie en supprimant : le signe   et parfois les parenthèses mais aussi en utilisant l’associativité et la commutativité de la multiplication.

Exemple 1 :    c’est une forme simplifiée de   

Grâce à l’associativité et la commutativité , « A » peut s’écrire       

En effectuant le calcul, on obtient :     qui s’écrit   :    

Règle :

Pour simplifier l’écriture d’un produit, on procède de la manière suivante :

    On effectue le produit de tous les nombres écrits en chiffres puis on écrit ce résultat suivi des lettres placées dans l’ordre alphabétique.

Activité 1 :

Simplifiez l’écriture  de

·      

·      

Exemple 2  : Simplifions l’écriture de     ;  est considéré comme 

On a alors       c'est-à-dire        

Activité 2 :

Simplifiez l’écriture  de

Exemple  3 :

Nous allons simplifier l’écriture  de  

On décompose :     ;  :

Activité 3 :

Simplifiez l’écriture  de

    ……………………………………………………………………….

Activité 4 :

Simplifiez l’écriture  de

Fiche  5  Attention : écriture qu’il ne faut pas confondre.

Par exemple :   

Deuxième exemple :     et comme  alors  :     

Donc 

Donc

    D’une manière générale , comparons  

   donc      

                          ;            est positif donc       est   négatif .   ;    

    Comparons maintenant :   (    et   

   donc     

Activité :

Complétez en mettant le signe

ATTENTION :

Dans chacune des lignes suivantes, une égalité n’est pas vraie pour tout «  » . Barrez – la .

Ligne 1

Ligne 2

Fiche 6 Ordre dans lequel il faut effectuer les opérations.

Info @.... »priorité..

Nous allons vous récapituler ici les règles que vous avez déjà rencontrées.

Règle 1 :

Dans une suite de calculs où figurent des parenthèses , on doit effectuer en priorité les opérations indiquées à l’intérieur .

( nota : les crochets sont des « super parenthèses » )

Exemple : …………………………………………………..

Règle 2 :

Dans une suite de calculs où figurent des multiplications et des additions ( ou soustractions) , mais pas de parenthèses , on doit effectuer en priorité les multiplications.

( On rétablit mentalement les parenthèses qui devraient figurer autour des nombres à multiplier ) .

La multiplication a priorité sur l’addition ( ou la soustraction )

Activité n° 1….

Calculez :

…………………………………….

Règle 3 :

En l’absence  de parenthèses , quand dans un calcul , il y a des multiplications et des « puissances » , on doit effectuer d’abord le calcul des puissances.

L’exposant s’applique uniquement au nombre qui le précède .

Activité n° 2 ….

Calculez :

Fiche   6 : Séries   d’exercices Types.

Exercices  série 1 :  ( exercices)

Sachant que  

Calculez   après avoir remplacé  par leur valeur.

Exercices  série 2 :

Faîtes de même avec    pour :

Exercice  3 :

Vous allez calculer :

Exercice  4 :

On vous demande de calculer :

Exercice  5 :

On vous demande de calculer  ; ( N’oubliez pas de simplifier toutes les fois que c’est possible )

Commencez par calculer   

Exercice  6 :

Vous allez calculer :

Exercice  7 :

Vous allez calculer :

Exercice  8 :

Vous allez calculer 

Fiche 7 : A propos de la simplification d’une somme  .

Rappel :

L’expression  s’appelle une  somme.    Est-elle simplifiable ?

Dans ce cas peut-elle s’écrire : «   »  ou «  »  ou   «   » ou «  » ?

Pour en avoir le cœur net , plaçons nous dans le cas   où  «  a = 9 »  et  « b = 6 ».

 432

= 810

 120

Vous constatez que dans chacun des cas , vous ne trouvez pas le même résultat que pour

Ces écritures ne désignent donc pas le même nombre. L’expression n’est donc pas simplifiable…..

Prenons  une autre expression :    .       (  désignant le même nombre )

Cherchons  si l’on peut dans ce cas  la simplifier .

Vous savez que       et     

Donc : :  

Grâce à l’associativité  de l’addition , on peut enlever les parenthèses , on a alors

   c'est-à-dire

A retenir :

Si   l’écriture     ne peut pas se simplifier

Par contre     s’écrit  

Fiche 8 : Distributivité de la multiplication sur l’addition .

Nous avons dans la classe de niveau immédiatement inférieur que :

«  » , «  » et « » désignant des nombres positifs  

« m » , « n » , « p »  désignant des nombres positifs  ,  

Ce qui est vrai pour les nombres positifs  l’ est aussi pour les nombres relatifs.

Activité n° 1

Vous allez le contrôler en complétant le tableau ci-dessous.

« k »

« a »

« b »

«  a + b »

«  k ( a + b )»

«  k a »

«  k b »

«  ka + kb »

-3

5

4

6

-3

-7

-5

-2

8

4

6

- 9

Colonne 1

Colonne 2

Activité n° 2 Comparez les résultats trouvés dans  les colonnes « 1 » et « 2 » .

…………………………………….

Il en serait de même pour tous les  nombres relatifs.

On dira alors :

(à retenir) .

La multiplication est distributive sur l’addition , cela signifie que :

·       «  » , «  » et « » désignant des nombres positifs

·       « m » , « n » , « p »  désignant des nombres positifs  ,  

On transforme ainsi le produit ( d’un nombre par une somme )  en une somme  ( dont les termes sont des produits de facteurs).

Quand on effectue cette transformation , on dit que l’on développe .

Activité n° 3 On vous demande de calculer « »  de deux façons différentes     «     »

Méthode n°1 : On effectue les calculs indiqués : 

Méthode n°2 : On développe :

  .  …………………………….

Activité n° 4  Faîtes de même pour : 

Méthode n°1 : On effectue les calculs indiqués :

Dans les parenthèses, on réduit au même dénominateur …..   …

..    ;   ..    ….    

Méthode n°2 : On développe :

=  = 

Activité n° 5 :   Développez  ( simplifiez l’écriture des produits ) 

 ……………………

( ………………………

………………..

…………………………..

…………………………….

Remarque :

Vous savez que «    ».

Ainsi , 

En développant on obtient : 

Vous retrouvez ainsi la règle de suppression des parenthèses précédées du signe  

Fiche  9 : La factorisation

Info +++@ factorisation..

«  » , «  » et « » ;       représentant  des nombres relatifs  vous savez que : 

et   

Réécrivez ces égalités  en intervertissant leurs membres :

On transforme ainsi une somme (dont les termes sont des produits de facteurs ) en un produit  ( dont l’un des facteurs est une somme de termes ) .

Quand on effectue cette transformation, on dit que l’on « factorise ».

Activité n° 1 :   En vous inspirant de ces égalités ci-dessus , complétez en factorisant : 

Schéma sur comment s’y prendre pour factoriser : 

Exemple 1 : On va factoriser :    

Nous allons chercher d’abord s’il y a un facteur commun , pour cela nous allons décomposer tous les termes de « A ».

Le facteur commun  est «  …. »

Dans chacun des trois  termes entourez le facteur commun.

                             Imaginez que vous enlevez  ce facteur commun pour le placer comme l’indique le schéma ci-dessus ( le rond) , ensuite , vous écrivez dans les parenthèses, les termes non soulignés.

D’où    :   

Contrôlez  en développant

Activité n°….  Factorisez ( écrivez directement le résultat )

Exemple 2 : Factorisons 

Constat : « G » est une somme de 3 termes et chacun de ces termes est un produit de facteurs.

Nous allons détailler ces produits pour faire apparaître tous les facteurs.

Ou   :  

Nous allons chercher les facteurs communs aux trois termes et soulignons – les .

·       Le facteur « 3 » se retrouve dans chacun des termes . Il faut le souligner.

·       Le facteur « a »  se retrouve  …… fois dans chacun des termes, il faut les souligner…..

·       Le facteur « b » se retrouve  …… fois dans chacun des termes , il faut le souligner….

·       Le facteur  « c » se retrouve …….. fois dans chacun des termes , il faut les souligner …….

Le produit de facteurs communs est alors :       soit    

En plaçant dans les parenthèses ce qui n’est pas retenu, on obtient :

Activité n°….    Faîtes de même pour

Détaillez les produits , soulignez les facteurs communs  et continuez comme précédemment.

·       Facteurs communs : ……………………………….

·       Soit le produit  de facteurs communs : 

Activité n°….    Faîtes de même  , factorisez  mentalement ……

Fiche  10 : Réduction de termes semblables.

Info +++@...

Avertissement : dans toute cette fiche , et sauf mention spéciale, les lettres désignent des nombres relatifs.

Vous savez que :    

Vous pouvez obtenir ce résultat en factorisant par «  »

Activité faites de même pour :

·       Dans le cas de   , vous constatez que l’on retrouve toujours    .

On dit qu’il s’agit d’une somme de termes semblables.

On dit que l’on a réduit les termes semblables.

·       Faîtes de même pour

·       Dans le cas de   il y a deux sortes de termes semblables.

Remarque :  Si vous pensez que le résultat peut s’écrire « 10 mp » ou «  24mp » , reportez-vous à la fiche 4 de ce cours……

Mais voici une autre explication

En convenant que « € » désigne 1 euro  et  «   » désigne 1 dollar , simplifiez l’écriture de :

  Ce que vous pouvez énoncer :   .

L’écriture 10 €$ aurait-elle cette signification dans ce cas ? ……………………………

Donc , pouvez-vous écrire le résultat de l’exercice précédent sous la forme de « 10 mp » ?   ……………….

Activité n° 1…..

Réduisez les termes semblables  de :

Activité n° 2…..

Réduisez les termes semblables  de :

Activité n° 3 …..

Développez et réduisez :

Activité n°4 …..

Développez et réduisez :

Activité n° 5…..

Développez et réduisez :

Activité n° 6 …..

Réduisez les termes semblables après avoir enlevé les crochets et les parenthèses :

Fin de ces travaux ..  ( sept.2014 )