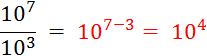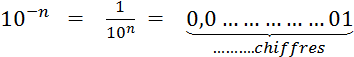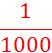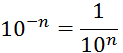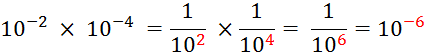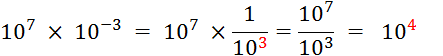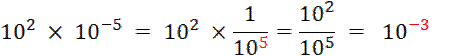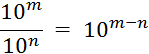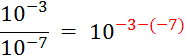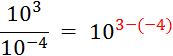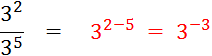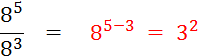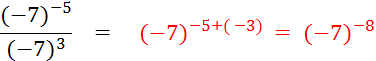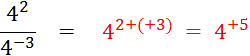Retour aux fiches sur ……….		Classe de collège 4^ème.
		CORRIGE.
Pré requis:
la multiplication de deux nombres relatifs	cliquer ici
Puissance « carrée »
Puissance « cube »
Puissance niveau 1 ( écriture normalisée )

ENVIRONNEMENT

Index : warmaths…

Objectif précédent : 1°) Puissances et écriture normalisée 2°) Multiplication de nombres relatifs cliquer ici 3°),Puissances avec des nombres relatifs.

Objectif suivant : Puissances ( carrés) d’opérations simples voir : l’exposant 0

INFO +++ : liste des cours sur les « PUISSANCES » Tableau 67

DOSSIE Fiches sur : PUISSANCE dont l’exposant est un entier relatif.

	Fiche 1 :Puissance de « 10 »
	Fiche 2 : Calculs sur les puissances de « 10 ».
	Fiche 3 : Puissances de « 10 » dans l’écriture d’un décimal.
	Fiche 4 : Utilisation des puissances de « 10 » dans les calculs.
	Fiche 5 : ORDRE ET NOMBRES ÉCRITS AVEC DES PUISSANCES DE 10 .
	Fiche 6 :Puissances entière d’exposant négatif d’un nombre quelconque.
TESTS	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
				Sciences PUISSANCE de dix (niveau II (6)) APPLIQUEES AUX SCIENCES

COURS :

1 - Puissance de « 10 »

Rappel : Complétez : ce qui s’écrit : « 1 » suivi de 3 zéros. ce qui s’écrit : « 1 » suivi de 7 zéros. ce qui s’écrit : « 1 » suivi de 0 zéros. (info @+exposant « 0 »+) Ainsi : «  » étant un entier naturel : s’écrit : « 1 » suivi de « » zéros.

Activités 1 : Complétez :

PUISSANCES DE 10 D'EXPOSANT ENTIER,NÉGATIF :

Par convention, on décide que « 0,1 » qui s'écrit s'écrira On définit de même ;  ; etc…..

; il y a 1 chiffre après la virgule. ; il y a 2 chiffres après la virgule. ; il y a 3 chiffres après la virgule.

« » étant un entier naturel non nul :

Complétez :

0, 000 000 000 001 =

Complétez le tableau des puissances successives de « 10 ».

Exposant

« -4 »

« -3 »

« -2 »

« -1 »

« 0 »

« 1 »

« 2 »

« 3 »

« 4 »

Puissance de 10

Ecriture fractionnaire

1

10

100

1 000

10 000

Ecriture décimale

0,000 1

0,001

0,01

0,1

1

Remarque : donc est ……l’inverse ……de 10 . Quel est l’inverse de  ? ……10……… . On peut donc écrire Donc sont inverse l’un de l’autre. Donc :

En généralisant : « » étant un entier naturel , c’est dire que Ce qui signifie sont inverse l’un de l’autre. Donc :

· Quel est l’inverse de  ? , ce qui s’écrit · Quel est l’inverse de  ? , ce qui s’écrit

v On peut donc dire : « n » étant un entier relatif quelconque ,

Vérifiez verbalement que l’égalité est bien vraie pour «   »

Fiche 2 : Calculs sur les puissances de « 10 »
Activité 1: Complétez :
v Il en serait ainsi quels que soient les exposants ; «  » et « » étant des entiers relatifs quelconques,
Activités 2 : Complétez :
=
Activités 3:
c'est-à-dire :			c'est-à-dire :
c'est-à-dire :			c'est-à-dire :
c'est-à-dire :			c'est-à-dire :
v Il en serait ainsi quels que soient les exposants. "" et   étant des entiers relatifs quelconques,
Activité 4 : Complétez :

Fiche 3 : Puissances de « 10 » dans l’écriture d’un décimal			Info +…..@...
4700 000 = 47 100 000 ; et comme 100 000 = ; alors 4700000 = 47
-583000 = -583 1000 ; et comme 1000 = - alors -583000 = -583
0,035 = 35 0,001 ; et comme 0,001 = " alors 0,035 = x
-0,7 = -7 0,1 ; et comme = alors -0,7 =
64,75 = 6475 0,01 ; et comme = alors 64,75 =
Tout décimal peut s'écrire sous forme de produit d'un entier (non divisible par 10) par une puissance de 10 dont l'exposant est un entier relatif.
Exercice 1 : Complétez
37 000 = 37	0,00043 = 43	-0,0085 = 85
- 4,85 = -485	230 = 23	3600 = 36
Exercice 2 : Ecrivez les nombres suivants sous la forme d'entier ou de nombre à virgule.
834 = 834 0000	- 0,0047 = 470	450 = 0,00450
- 62 = - 0,62	0,071 = 0,0000 071	- 5,43 = - 0,0543
34,7 = 3,47	43,59 = 43,59	6300 = 6 300 000
Remarque « 38000000 » peut s'écrire 38 x 10^6 mais aussi 3800 x 10^4 ou 0,038 x 10^9 ou encore 38000000000 x 10^-3
Exercice 3 : Complétez en vous inspirant de la remarque précédente.
69 000 = 69 = 690 = 0,000 69 = 6 900 000
17,38 = 1738 = 1,738 = 0,001738 = 1 738 000
341 = 341 = 3,41 = 0,000 341 = 341 000
0, 052 = 52 = 5,2 = 0,0052 = 520000

Fiche 4 : Utilisation des puissances de « 10 » dans les calculs.
Problème 1. L'analyse du sang d'une personne a révélé que dans chaque mm^3 de sang, il y avait 4830000 globules rouges. Combien cette personne possède-t-elle environ de globules rouges sachant que le corps humain contient environ 5 L de sang ? On rappelle que 1 L = 1 dm^3, donc 5 L =________________________________________________________________ mm^3.
Pour résoudre ce problème, Pierre prend sa calculatrice (non scientifique) et tape 5000000 x 4830000. La machine affiche | 99 999 999 | et clignote . Ce qui signifie un dépassement de capacité de la machine. * On peut éviter cet inconvénient en utilisant des puissances de 10.
5000000 = 5 x 10 ^6 et 4830000 = 483 x 10^4 . On peut écrire alors : 5000000 4830000 = (5 10 ^6 ) (483 10^4) = (5 483) (10 ^6 10^4 ) Or : 5 x 483 = 2 415 et (10 ^6 10^4 ) = 10^10 donc 5 000 000 x 4 830 000 = 2 41510^10 Réponse : Nombre de globules rouges : 24 150 000 000 000.
Activité 1 : Calculez de même : 21 000 x 4 000 000 =……………. 10^… ……….. 10^… = ……………. 10^…
700000 x 30000000 =
Ecriture en notation scientifique.	Info ++@ +++++
Lucile résout aussi le problème. Elle tape 5 000 000 x 4830000. Sa calculatrice scientifique affiche		2.415 13
Ce qui signifie 2,415 x 10 ^13 . 2,415 x 10 ^13 . est l'écriture scientifique du nombre 24 150000000000. Cette écriture est constituée par le produit d'une puissance de 10 et d'un nombre ayant 1 chiffre non nul avant la virgule. Exemples : L'écriture scientifique de 357600 est 3,576 x 10^6 . Celle de 687,54 est 6,8754 x 10^2 De même pour les négatifs, l'écriture scientifique de - 9612 est -9,612 x 10^3
Exercice 2 : Donnez l'écriture scientifique : 87400000 = -6534,87 = ; -734857 = ; 534 x 107 =
Problème 2 Un globule rouge a sensiblement la forme d'un cylindre dont la hauteur est 0,0027 mm et dont l'aire de la base circulaire est 0,000034 mm". Quel est le volume d'un globule rouge en mm^3 ? Lucile prend sa calculatrice (non scientifique) et tape 0,0027 x 0,000034 , La machine affiche | 0.0000000 | et clignote. Ce qui signifie un dépassement de capacité de la machine. On peut éviter cet inconvénient en utilisant des puissances de 10 : 0,0027 = 27 10^-4 et 0,000034 = 34 10 ^- 6 . On peut écrire alors : 0,0027 x 0,000034 = ( 27 10^-4) x (34 10 ^– 6) ( 27 34 ) (10^-4 10 ^– 6 ) Or 27 x 34 ……918…….. et (10^-4 10 ^– 6 ) = 10 ^– 10 ; = donc = 918 10 ^– 10 Réponse : Volume d'un globule rouge (en écriture décimale) : 0,000 000 091 8
Exercice 3 Calcule de même 0,000 13 0,0000037 13 10 ^-5 37 ___________________________________________________ 10 ^-7= 481 10^-10 0,025 x 0,0008 =____________________________________________
Ecriture en notation scientifique. (suite )
Sur sa calculatrice scientifique, Léonie tape 0,0027 x 0,000034 . La machine affiche | 9.18 – 08 ] Ce qui signifie 9,18 10^-8 . 9,18 x 10^-8 est l'écriture scientifique du nombre 0,000000091 8
Exercice 4 Donnez l'écriture scientifique 0,0000437 =____________ -0,00057 »________________________________________ Idem : 0,361 =_________________ 0,0082 x 10^-4 =_______ …………………………………………………
Activité : Calculez 5,23 10^-3 4,28 10^7 = Idem : 2,7 10^4 6,1 10^-6 =

Fiche 5 : ORDRE ET NOMBRES ÉCRITS AVEC DES PUISSANCES DE 10 .
COMPARAISON DE NOMBRES EN ÉCRITURE SCIENTIFIQUE :
Comparons 8,745 10^-5 et 4,328 10^-4 . Il suffit de comparer les puissances de 10.
Puisque « -5 » «  -4 » alors 10 ^–5 10 ^– 4 donc 8,745 10^-5 4,328 10^-4 .
Comparons : 3, 7 10 ^3 et 3 , 45 10 ^3 . La puissance de "10" est la même , on compare « 3,7 » et « 3,45 » . On a alors : 3, 7 10 ^3 3 , 45 10 ^3 Exercice : Rangez dans l’ordre croissant :
3,45 10 ²	-7,3 10 ^-3		-8,17 10 ^2	4,7 10 ^-4	3,6 10 ^3	-4,2 10 ^-2	-7,23 10 ^-3
UTILISATION DES PUISSANCES DE « 10 » DANS LES ENCADREMENTS
Activité : Complétez l'encadrement de ; = 3,1415927…………………………….. en utilisant les deux notations suivantes :
« 3 » < < «  4 »		« 3 » < < «  4 » à « 1 » près.
« 3,1 » < < «  3,2  »		« 31 10 ^-1 » < < « 32 10 ^-1 » ; à « 10 ^-1 » près.
« 3,14 » < < «  3 ,15  »		« 314 10 ^-2 » < < « 315 10 ^-2 » ; à « 10 ^-2 » près.
« 3, 141  » < < «  3, 142  »		« 3141 10 ^-3 » < < « 3142 10 ^-3 » ; à « 10 ^-3 » près.
ORDRE DE GRANDEUR :
L'écriture scientifique d'un nombre donne un ordre de grandeur du nombre : = 4,17 10^3 ; Ordre de grandeur 10^3. est de l'ordre des milles
« » 3 , 538 10 ^-2 ; ordre de grandeur 10 ^-2 … ; «  » est de l’ordre des centièmes.
« » = 1, 837 10 ^6 ; ordre de grandeur 10 ^6 … ; «  » est de l’ordre des millièmes .

Fiche 6 :Puissances entière d’exposant négatif d’un nombre quelconque.
Vous avez vu ( dans la fiche 1 ) que , par convention, . ( 10 ^-1 est l’inverse de 10 ) On décide d’étendre cette notation à tous les nombres relatifs non nuls.
«  » étant un nombre relatif non nul ; . ( ^-1 est l’inverse de )
Activité : 5 ^-1 ; 0,9 ^-1 = ; ( - 6 ) ^-1 = ; = ; =
v Plus généralement, «  » étant un entier relatif quelconque, on a vu que : On dira de même pour un nombre relatif «  » » non nul:
«  » étant un nombre relatif non nul , : ; «  ^–n » est l’inverse de «  ^n »
Exemples : 4 ^-3 ; ( 0,5 ) ^– 4 ; ( - 2 ) ^– 5 ; ;
CALCULS AVEC DES EXPOSANTS NÉGATIFS
Les règles de calculs sont les mêmes que pour les puissances de « 10 » .
Activité : Complétez :
7 ^– 6 7 ^2 = = =	4 ^– 5 4 ^-2 = = =	( - 6 ) ^3 ( - 6 ) ^- 8 = ( - 6 ) ^???