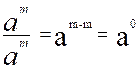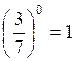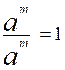Information

L’exposant zéro a son origine dans l’application de la règle des exposants au cas de la division d’une quantité  affectée d’un certain exposant  par la même quantité affectée du même exposant.

Cette règle appliquée à la division    donne ,en effet,

Valeur conventionnelle :

Le symbole B⁰  n’a aucun sens par lui –même ; mais on a adopté la convention suivante :

Toute quantité affectée de l’exposant zéro représente l’unité positive .

Par exemples  :   ⁰ = 1   ; ( ) ⁰  = 1 ;      ;  ( - a ) ⁰ = 1

Cette convention est naturelle.

En effet , d’abord  elle identifie le résultat de la règle des exposants :  a ^m : a ^m = a ^m-m  =  a ⁰   , avec la valeur vraie du quotient : toute quantité divisée par elle-même donne pour quotient l’unité positive , 

Rappel : l’exposant est une quantité ,ordinairement numérique ,qu’on écrit à droite  et un peu au dessus d’une autre quantité pour indiquer combien de fois celle-ci doit entrer comme facteur dans le produit.

Fin du rappel.

L’exposant 0 indique la quantité qu’il affecte doit entrer O fois comme facteur dans le produit considéré.

Exemples :  3 a ²  b⁰ c  = 3 a ²  c = 3 a ² x 1 x  c   ;   a ⁰ = + 1  a ⁰  =  + 1 

Utilité :

L’introduction de l’exposant « 0 »   et la convention  A⁰ = 1  offre de précieux avantages .

Ainsi ,

 1 ⁰  ) on pourra considérer tout facteur qui fait défaut dans un terme  comme y figurant avec l’exposant zéro : a ² + 2 ab + b²  =  a ² b⁰ + 2 ab + a ⁰ b² ;  x² + 2x + 1  = x² + 2x + x⁰

cette convention permet de conserver , parfois très utilement ,la trace d’un facteur qui sans cela disparaîtrait dans la suite des calculs.

2°) On pourra simplifier et généraliser  les énoncés de certaines règles .Ainsi les règles de multiplication et de la division des monômes s’énonceront :

Pour multiplier deux monômes ,il suffit de multiplier les coefficients , d’ajouter les exposants et d’appliquer la règle des signes.

Pour diviser deux monômes , il suffit de diviser les coefficients , de soustraire les exposants et d’appliquer la règle des signes.

Exemples :

2 a² b²  3 a c = 2   3 a² ⁺¹ b ³⁺⁰ c ⁰⁺¹  =  6 a³ b ³ c ;

^{3     3-22-210}

L’exposant zéro constitue une première généralisation des exposants. Qui se complétera par l’introduction des exposants négatifs et des exposants fractionnaires.