la droite des milieux dans le triangle, au 4ème collège- corrigé

	Retour vers les fiches de travail.	Classe de 4^ème Collège.
	Fiches :CORRIGE	Programme @ Classe 4^ème collège.

Pré requis:
la médiatrice
Caractéristiques du Triangle

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent

Objectif suivant :

Division d’un segment.

voir « propriété de Thalès appliquée aux triangles »

tableau

Tout sur les triangles.(liste)

	DOSSIER géométrie plane : La DROITE des MILIEUX dans le triangle.

	Fiche 1 : Application de la propriété sur la projection du milieu d’un segment. ( voir le théorème 1)
	Fiche 2 : Exercices (sur l’ utilisation du théorème 1).
	Fiche 3 : Droites des milieux dans le triangle . (Théorème 2 : dit « Théorème de la droite des milieux » ).
	Fiche 4 : Exercices types. ( avec utilisation du théorème n°2 )

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

	Connaître et utiliser les théorème suivants relatifs aux milieux de deux côtés d’un triangle . Résumé à retenir : Théorème 1 : Dans un triangle , si une droite passe par les milieux de deux côtés , elle est parallèle au troisième . Théorème 2 : Dans un triangle , si une droite passe par le milieu d’un côté et est parallèle à un second côté , elle coupe le troisième en son milieu. Théorème 3 : Dans un triangle , la longueur du segment joignant les milieux de deux côtés est égale à la moitié de celle du troisième côté.

	COURS.

	Fiche 1 : Application de la propriété sur la projection du milieu d’un segment.		Info +fiche 4 +

	On vous a dessiné ci-contre un triangle « ABC » , « M » est le milieu de [ AB ] . On vous demande de tracer la parallèle à [ BC ] . Elle coupe [ AC ] en « N ». Démontrez que « N » est le milieu de [ AC ].
	- Hypothèse : -………………………………………………………………………… ……………………………………………………………………………… - Conclusion ……………………………………………………………….
	Démonstration : Par hypothèse , ( MN ) et ( BC ) sont parallèles , elles ont donc même …….direction…….. Dans la projection de ( A B ) sur ( A C ) suivant la direction de ( M N ) et ( B C ) , « A » à projeté « A » ; « M » à pour projeté « N » et « B » à projeté « C ». Le projeté de [AB] est donc [ AC ] .Par hypothèse « M » est milieu de de [AB] D’après la propriété sur la projection du milieu d’un segment , le milieu « M » de [AB] se projette au milieu de [ AC ] Or , le projeté de « M » est « N » , donc « N » est ….milieu de [ AC ] …

	Théorème 1 : Dans tout triangle , si une parallèle à l’un des côtés passe par le milieu d’un autre côté alors , elle passe par le milieu du troisième côté.

	Remarque : Toutes les fois que dans un problème on sera dans la situation de l’hypothèse du théorème ci-dessus, on pourra affirmer que la conclusion correspondante est vraie sans avoir besoin de refaire la démonstration puisque celle-ci vient d’être faite une fois pour toutes. On dira que l’on « applique le théorème 1 ».
	Activité : Ci-contre un triangle « ABC ». « D » est un point quelconque de [ BC ]. Soit « M » le milieu de [ BD ]. Tracez par « M » la parallèle à ( BA ) qui coupe ( AD ) en « E ». Tracez par « E » la parallèle à ( A C ) qui coupe ( DC ) en « N ». Démontrons que "N" est le milieu de [ DC ].
	- Hypothèse : -………………………………………………………………………… - ……………………………………………………………………………… Conclusion ……………………………………………………………….

	Recherche . ( A ne pas écrire dans la rédaction d’un devoir ). On veut démontrer que « N » est le milieu de [ DC ]. Pour cela, on va essayer de faire apparaître la situation du théorème 1. Il faut alors trouver un triangle dans lequel une droite parallèle à l’un des côtés et passe par le mileiu d’un autre côté de telle sorte qu’elle coupe [ DC ] en son milieu. Or on sait par hypothèse que ( EN ) est parallèle à …( AC ) …., si l’on peut prouver que « E » est milieu de [ AD ] , alors en appliquant le théorème 1 au triangle …….., on pourra affirmer que « N » est le milieu de … [ DC ].…… Il reste à prouver que « E » est le milieu [ AD ] . Faites le oralement… !!!!.

	Démonstration : Dans un triangle « ABD » par hypothèse « M » est le milieu de ……[ BD ]…… et ( ME) est ………parallèle …. à ( AB), donc d’après le théorème 1 , « E » est le …. milieu …. de …[ AD ] …..et puisque ( EN ) est ..parallèle ….. à ( AC ) . ( par hypothèse ) , alors d’après le théorème 1 , « N » est le milieu de …[ DC ]….

	FICHE 2 : Exercices ( utilisation du théorème 1).
	Activité 1 : Deux droites « d » et « d’ » se coupent en « O ». « A » et « B » sont deux points de « d » tel que « A » soit le milieu de [ OB ] . Tracez par « A » et « B » deux parallèles qui coupent respectivement « d’ » en « C » et « D ». Tracez par « D » la parallèle à ( C B ) qui coupe « d » en « E ». Démontrez que « B » est le milieu de [ OE ].

	Activité 2 : On donne un triangle « ABC ». « M » est le milieu de [ BC ]. « N » est le milieu de [ AB ]. Tracez par « N » la parallèle à ( BC )qui coupe ( A M ) en « P ». Tracez ( C P) qui coupe ( AB ) en « E ». Par « M » , tracez la parallèle à ( C P ) qui coupe ( A B ) en « F ». 1°) Démontrez que « P » est le milieu de [ AM ]. 2°) Démontrez que « E » est le milieu de [ AF ]. 3°) Démontrez que « F » est le milieu de [ EB ].


	Fiche 3: Droites des milieux dans le triangle.

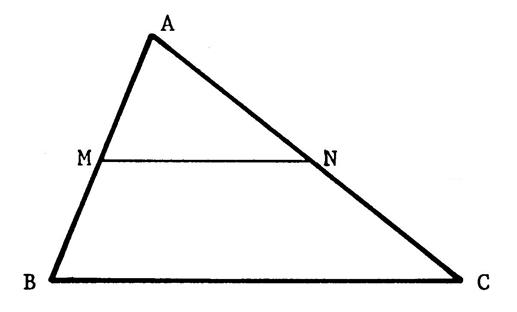
	Voici un triangle « ABC » « M » est le milieu de [ AB ] « N » est le milieu de [ AC ] Nous démontrons que ( MN ) est parallèle à ( BC ) Hypothèse : - - Conclusion :
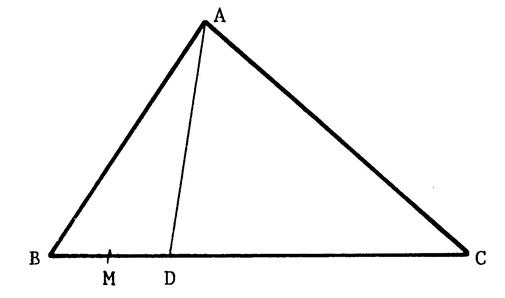
	Démonstration : Considérons la projection de (AB) sur (AC) selon la direction de la droite ( BC). « A » a pour projeté ……….. « A »… Le projeté de [ AB ] est [ AC ] . D’après la propriété « 7 » , on peut dire que : Le point « M » milieu de [ AB ] se projette au milieu de [ AC ] qui est le point « N ». Donc la droite ( MN ) est la projetante de « M ». Elle a donc la même direction que ( BC ) Donc ( M N ) et ( BC ) sont parallèles.
	Théorème 2 : dit « Théorème de la droite des milieux » Dans tout triangle , si une droite passe par les milieux de deux côtés , alors elle est parallèle au troisième côté.
	Remarque : ce théorème servira à prouver dans certains cas que deux droites sont parallèles.
	Activité n° :
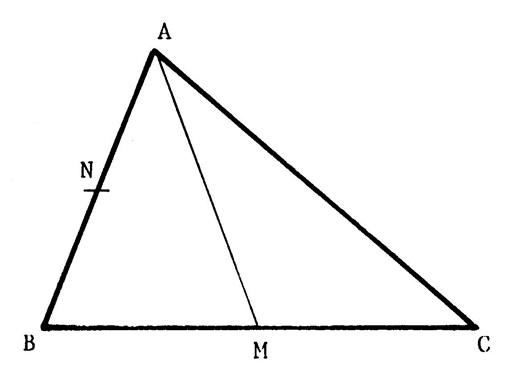
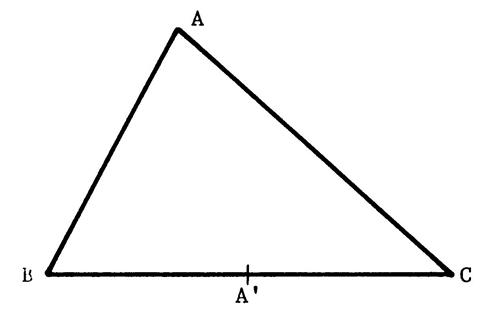
	Ci-contre : Voici un triangle ABC. « A’ » est le milieu de [ BC] La parallèle à ( AB ) passant par « A’ » coupe ( AC ) en « B’ » La parallèle à ( BC ) passant par « B’ » coupe ( AB ) en « C’ ». Démontrez que ( A ' C ' ) est parallèle à ( A C ). Hypothèse : ........ …… Conclusion : ……………………….
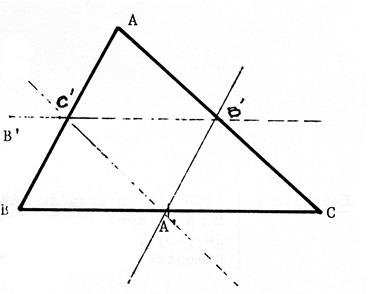
	Commentaire : A ne pas écrire dans la rédaction d’un devoir). On peut démontrer que ( A’C’) est parallèle à ( AC ). Pour cela , on va essayer de faire apparaître la situation du théorème 2 : « Dans tout triangle , si une droite passe par les milieux de deux côtés , alors elle est parallèle au troisième » Il faut donc trouver un triangle dans lequel ( A ‘ C’ ) passe par les milieux de 2 côtés. Or, on sait par hypothèse que « A’ » est le milieu de [ BC ] , l’on peut prouver que « C’ » est le milieu de [ BA ] , alors en appliquant le théorème n° .2 . au triangle …ABC… , on pourra affirmer que ( A ‘ C’ ) et parallèle à ( A C ) .
	Il reste à prouver que « C’ » est le milieu de [ BA ]. Pour cela, on pense au théorème n° 1 : . Il faut alors trouver un triangle dans lequel une droite est parallèle à l’un des côtés et passe par le milieu d’un autre côté de telle sort qu’elle coupe [ BA ] en son milieu.
	Corrigé : Démonstration : Dans le triangle « ABC » : Par hypothèse : « A’ » est le milieu de [ BC ] et ( A’ B’) est parallèle à ( AB ) , donc d’après le théorème n° .1. , « B’ » est le milieu de [BC] . Dans le triangle « ABC » , on vient de dire que « B’ » est le milieu de [BC] et on sait que par hypothèse que ( B’ C’) est parallèle à [BC] .donc d’après le théorème N° …. , … « C’ » est le milieu de [ BA ] ………………………………………………………………. Dans le triangle « ABC » , on sait par hypothèse que « A’ » est le milieu de [BC] . et on vient de prouver que « C’ » est le milieu de [ BA ] donc d’après le théorème n°.2. , la droite ( A’C’) est parallèle à [AC]

	Fiche 4 : Exercices types. ( avec utilisation du théorème n°2 ) « Dans tout triangle , si une droite passe par les milieux de deux côtés , alors elle est parallèle au troisième »
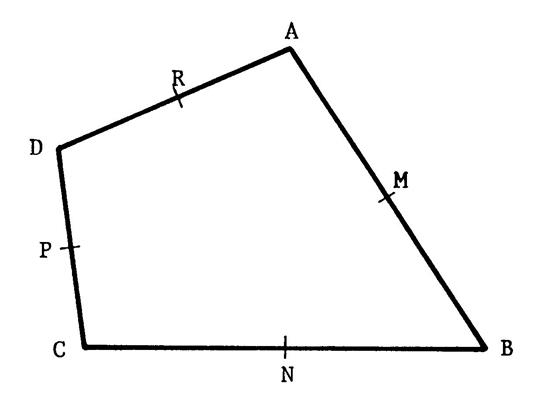
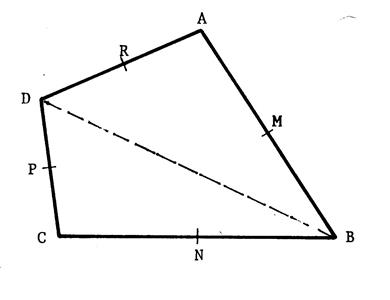
	Exercice 1 : Ci-contre on vous a représenté un quadrilatère quelconque « ABCD » . « M », « N », « P » et « R » sont les milieux respectifs de [ AB ]. [ BC ]. [ CD ]. [ DA ]. Démontrez que (MR) est parallèle à ( N P )et que ( MN ) et parallèle à ( RP ) . Indication : Il faut considérer successivement les triangles « ABD » et « BCD » dans lesquels on appliquera le théorème n°2. Grâce à la transitivité du parallélisme, on en déduit que ( MR ) est parallèle à (NP). On effectuera la même démonstration pour ( MN ) et ( RP ).


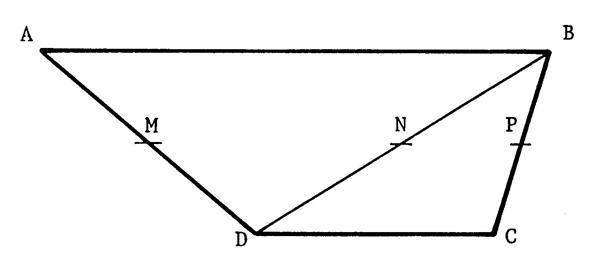
	Exercice n°2 : « ABCD » est un trapèze ( AB ) // ( CD). « M », « N », « P » sont les milieux respectifs de [ AD ] , [ BD ] , [ BC]. Démontrez que « M » , « N » et « P » sont alignés .

TRAVAUX AUTO- FORMATIFS.

CONTROLE:

1°) Compléter les phrases suivantes :

La droite qui relie les milieux de deux cotés d’un triangle ……………côté.

2°) Le segment qui relie les milieux de deux côtés d’un triangle a une longueur égale ……………… de la longueur du troisième coté.

3°) Citer les 3 théorèmes relatifs « aux milieux »

EVALUATION:

1°) Tracer un triangle quelconque : et tracer les droites des milieux .

2°) Droite des milieux d' un triangle .

a) Construire un triangle de côtés AB = 6 cm , BC = 7 cm et AC = 8 cm . Placer le point M au milieu du segment [ AB ] et tracer la parallèle à [ BC] qui coupe [A C] en N .

b)Appliquer la relation de Thalès pour prouver que N est le milieu de [ AC] . La droite ( MN ) est dite « droite des milieux » .

b) Construire les deux autres droites des milieux du triangle .

COURS.