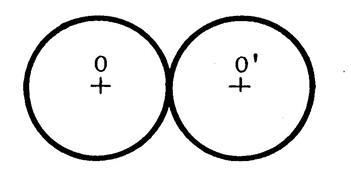Fiche 1 :  Centre de symétrie du cercle.

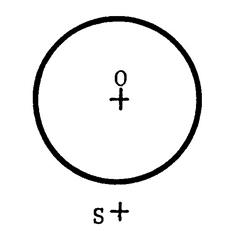
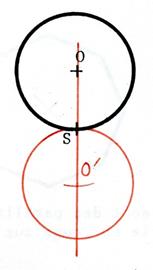
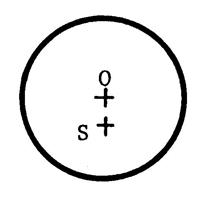
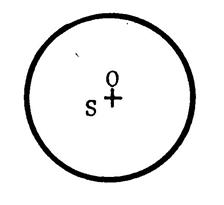
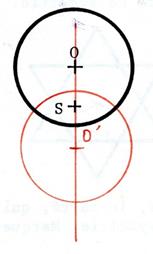
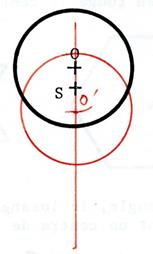
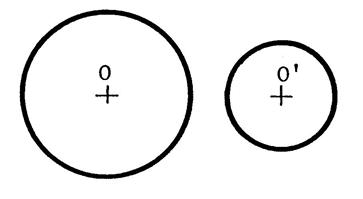
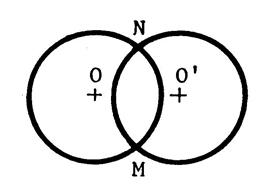
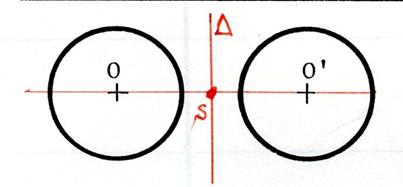
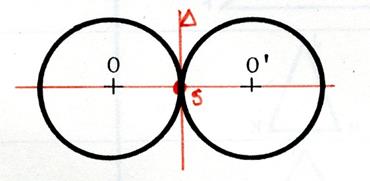
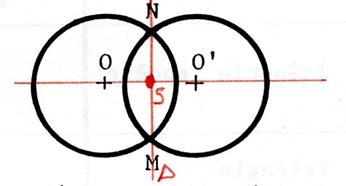
Dans chacun des cas  ci-joint , dessinez l’image du cercle de centre « O » dans la symétrie centrale de centre « S ».

Appelez « O’ » le symétrique de « O ».

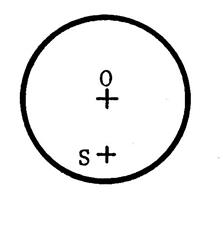
Vous constatez que dans le cas où le centre de symétrie est confondu avec le centre du cercle, alors le cercle et son symétrique sont …..confondus….

On dit que le centre du cercle est centre de symétrie pour le cercle….

Fiche 2 : Centre de symétrie du parallélogramme. 

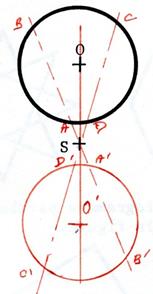
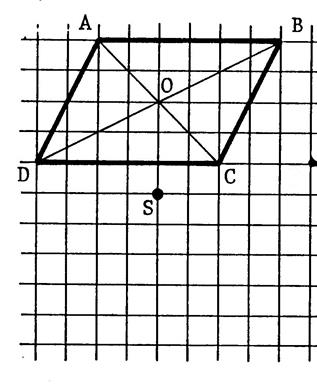
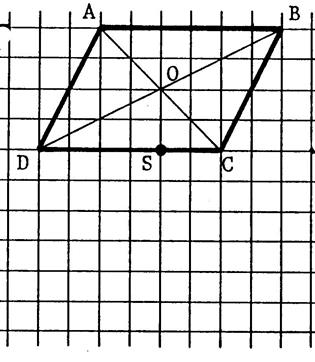
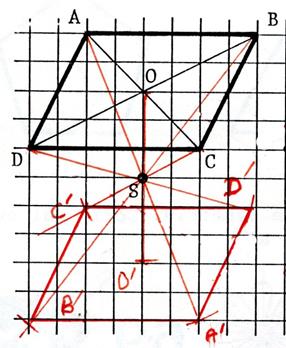
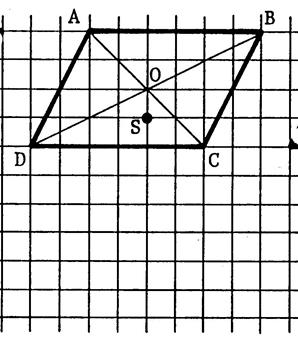
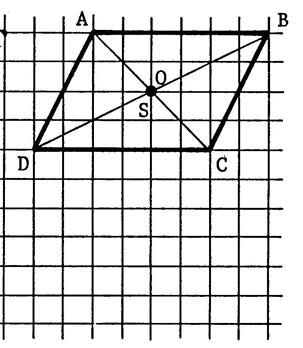
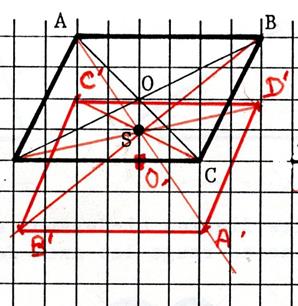
Dans chacun des cas ci-dessous , dessinez l’image du parallélogramme  « ABCD » de centre « O » dans la symétrie centrale de centre « S ».

Appelez «  A’ ; B’ ; C’ ; D’ , O’ » les symétriques.

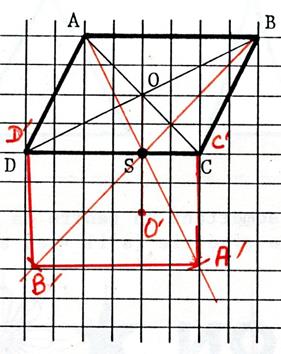
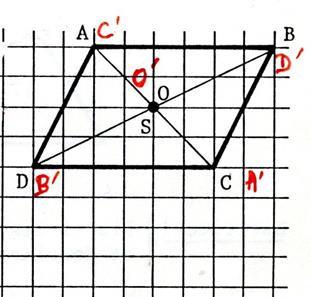
Vous constatez que dans le cas où le centre de symétrie est confondu avec le centre du parallélogramme, alors le parallélogramme et son symétrique sont confondus..

Nous allons vous confirmer cette constatation par un raisonnement.

« O » étant le centre du parallélogramme  «  ABCD » , alors « O » est le milieu de [  AC ] et de [ BD ].

Donc « A » et « C » sont symétriques par rapport à « O »  et « B » et « D » sont symétriques par rapport  à « O » .

Donc [  AB ] et de [ CD ]  sont symétriques  par rapport à « O » , ainsi que [  AD ] et de [ CB ].

Le parallélogramme « ABCD » est donc confondu avec son symétrique par rapport à « O ».

On dit que le point « O » est centre de symétrie  pour le parallélogramme.

Fiche 3  Centre de symétrie d’une figure.

SOS info La symétrie centrale…

Il n’y a pas que le cercle et le parallélogramme qui admettent un centre de symétrie. D’une manière générale :

Dire que : « une figure admet un point pour centre de symétrie » c’est déclarer que la figure est sa propre symétrie par rapport  à ce point.

Dans ce cas , tout point de la figure a pour symétrique un point de la figure.

Exemples :

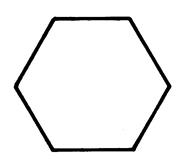
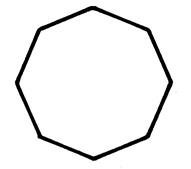
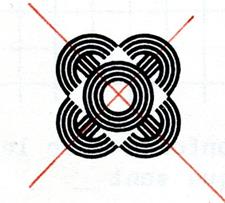
Voici des figures qui admettent un centre de symétrie.

L’ hexagone

L’ octogone

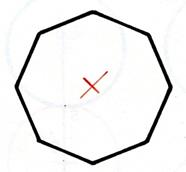
Régulier  convexe

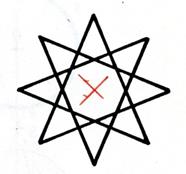
Régulier  croisé

Régulier  convexe

Régulier  croisé

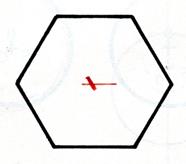
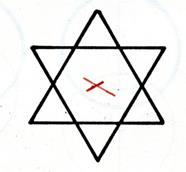
Activité : on vous demande de marquer en rouge le centre de symétrie.

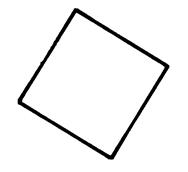
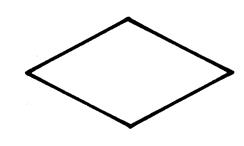
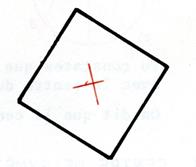
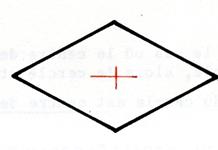
·       Le rectangle , le losange , et le carré  qui sont des parallélogramme particuliers, admettent un centre de symétrie.

Activité : on vous demande de marquer en rouge le centre de symétrie.

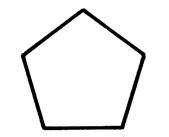
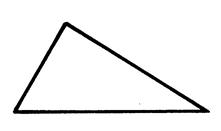
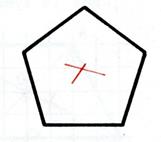
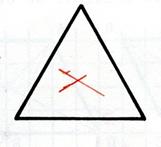
Ci-dessous , voici  un pentagone et  des triangles : isocèle ; quelconque et équilatéral .

Activité n°… : cherchez s’ils admettent des centres de symétrie ( écrivez « oui » ou « non » sous la figure.

………oui………..

…………non pas de centre,

Mais un axe………..

………non……………

…………oui……….

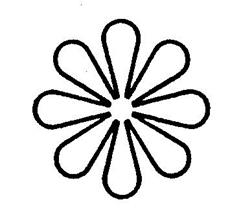
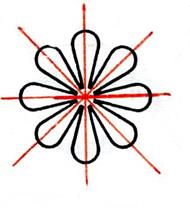
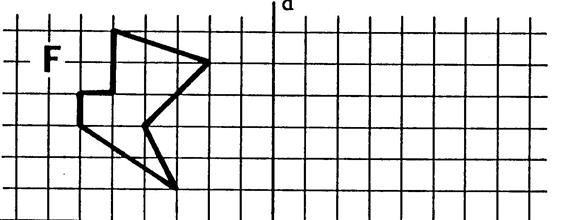
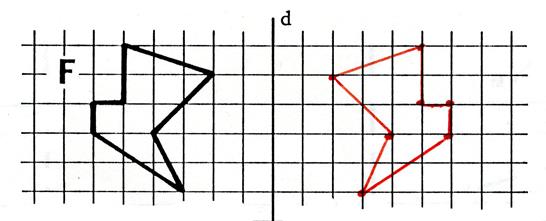
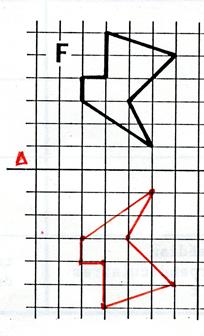
Activité n°… : Dites si les figures  ci-dessous admettent un centre de symétrie ( écrivez : « oui » ou « non »)  et dessinez en rouge les axes de symétrie. ( si ils en possèdent)

………………..

………………

………………….

………………….

………………

………………..

……………………

……………………..

Activité n°… : Certaines lettres majuscules admettent un centre de symétrie.

Ecrivez ci-dessous celles que vous avez trouvées.

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

Fiche 4 : Axes et centres de symétrie de figures élémentaires.

Activités n°….travaillez sur la fiche suivante…….

·       Complétez les dessins en traçant ( en rouge) les axes de symétrie. ( s’il y en a une infinité, vous n’en tracez que quelques-uns)

Placez aussi ( en rouge) les centres de symétrie.

·       Dans les deux autres colonnes ; nommez les axes de symétrie et dans l’autre nommez les centres de symétries.

·       Nota : s’il n »y a pas de symétrie ou de centre de symétrie, vous écrivez « aucun ».

·       On vous donne deux exemples : le cercle et la paire de droites parallèles.

·       Et dans le cas des droites parallèles , tracez l’axe médian…….

Intitulé de la situation

Dessin

Axe de symétrie

Centre de symétrie

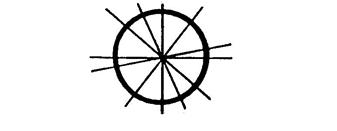
Cercle

Toutes les droites diamétrales

Le centre du cercle.

Droite

Les perpendiculaires à « d »

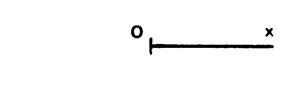
Demi-droite

O

Segment

« A » ou « B »

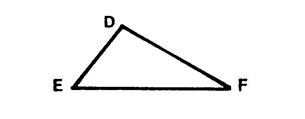
Triangle quelconque

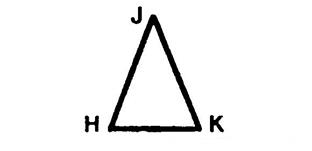
Triangle isocèle

La perpendiculaire à « HK » passant par « J »

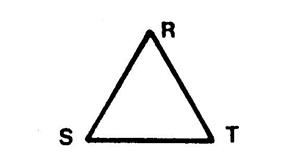
Triangle équilatéral

Toutes les perpendiculaires passant par les sommets…

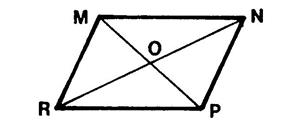
Parallélogramme

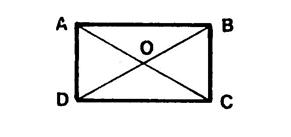
Rectangle

Losange

Carré

Paire de demi-droites

Paire de droites sécantes

Paire de droite de droites parallèles

-         L’axe médian

-         Les perpendiculaires à « d »et « f »

Tous les points de l’axe médian .

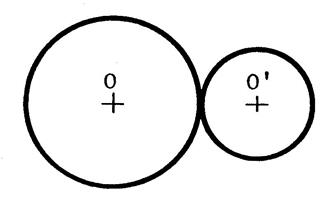
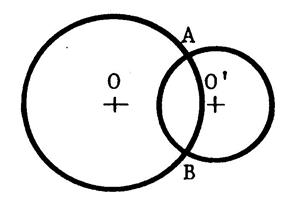
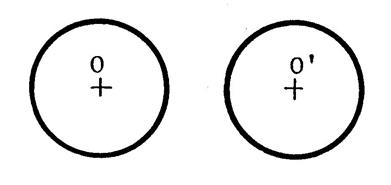
Fiche 5 : Symétrie  pour deux cercles.

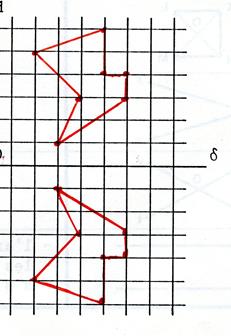
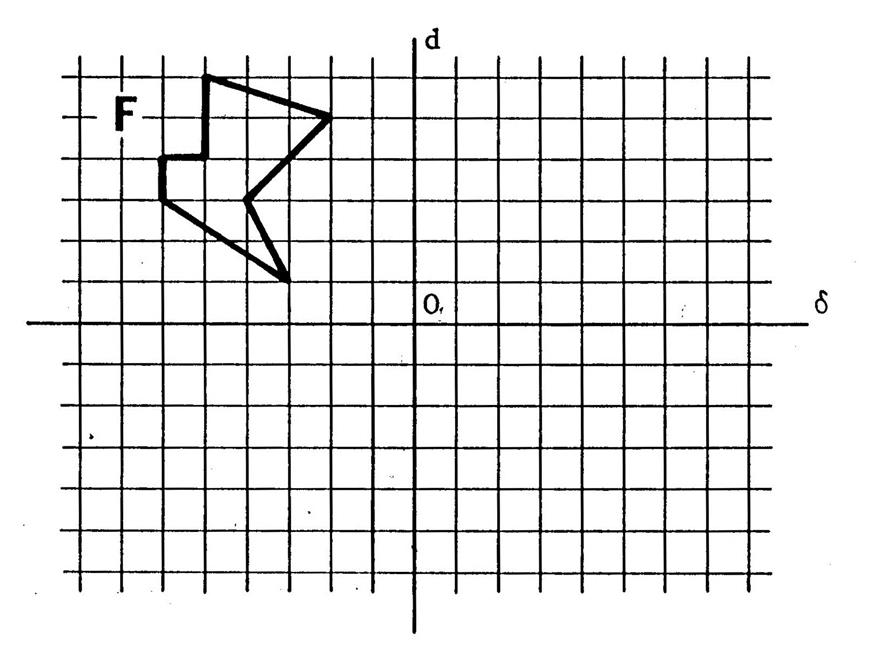
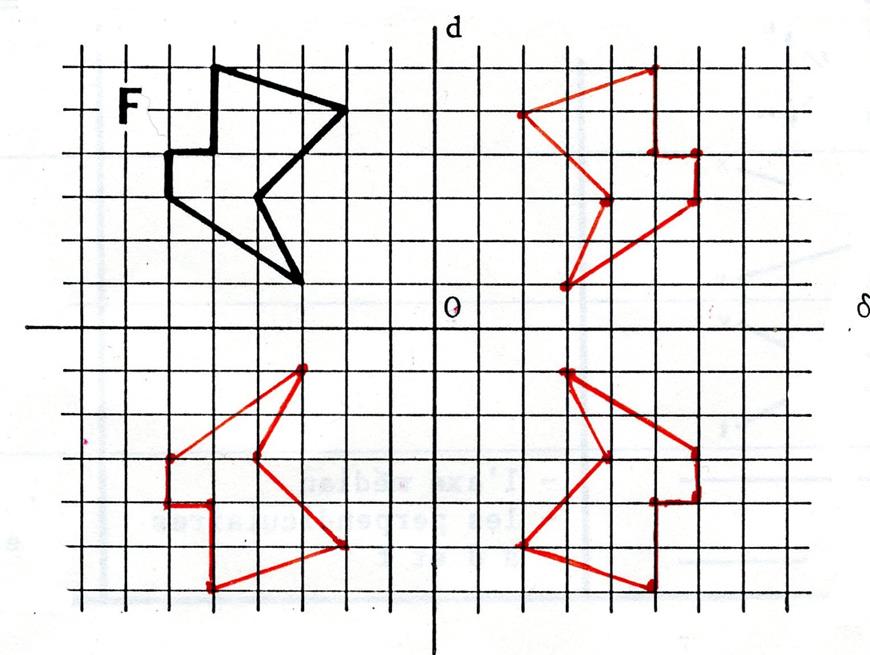
Fiche 6 : Symétries orthogonales à axes perpendiculaires.

28 / 12/ 2013