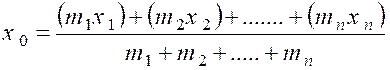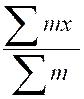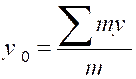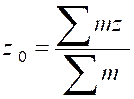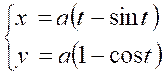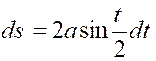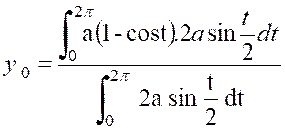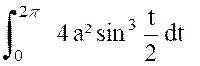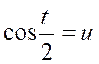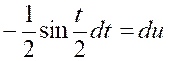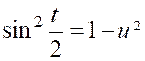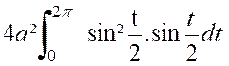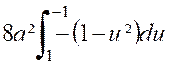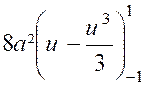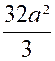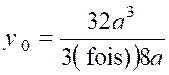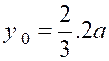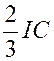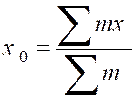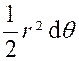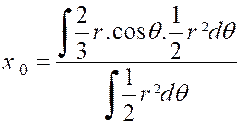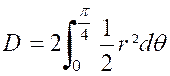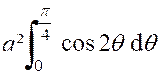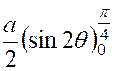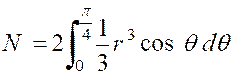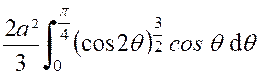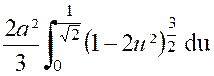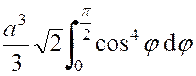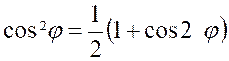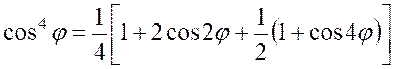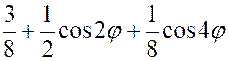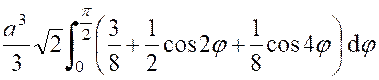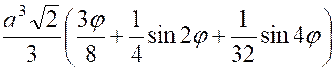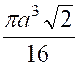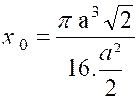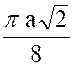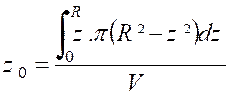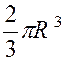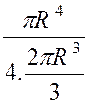Généralités .

Exemples :

• Trouver le centre de gravité de l’arc cycloïde .

• Trouver le centre de gravité de l’ aire d’une boucle de la lemniscate

• Calculer le centre de gravité du volume d’une demi -sphère de rayon « R »

COURS

Généralités

On sait que étant  donnés « n » points  « P₁ » , « P₂ » ;….. »P_n » de masses  respectives  « m₁ ;  «  m₂ » ;….. ; « m_n » et de coordonnées ( x ₁ ; y ₁ ; z ₁ ) ; ( x ₂ ; y ₂ ; z ₂ ) ;…… ;( x _n ; y _n ; z _n ) ;. Les coordonnées ( x ₀ ; y ₀ ; z ₀ ) de leur centre de gravité « G » sont donnés par les formules :

  =    .   

Le signe «  »  (sigma) exprimant que l’on doit faire la somme des quantités analogues en étendant  cette somme à tous les points donnés, et de même :

«  »    et  «  

Nous ne considérons que des corps homogènes , c'est-à-dire des corps ayant, en tous leurs points,la même densité.

Nous ne changerons donc pas la position du centre de gravité en remplaçant la masse par la longueur , la surface ou le volume suivant qu’il s’agit d’un arc , d’une aire ou d’un volume.,

En effet ,ceci revient à modifier toutes les masses dans le même rapport et cette opération ne change rien aux valeurs de  ( x ₀ ; y ₀ ; z ₀ ).

Exemple 1 :

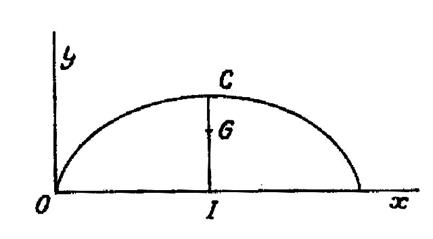
Trouver le centre de gravité de l’arc cycloïde :

   ( voir la figure ci contre)

Remarquons d’abord que le centre de gravité de l’arc « OGB » se trouve sur la droite «  », qui est un axe de symétrie de la courbe.

Nous n’avons donc qu’à calculer l’ordonnée.  du point cherché.

D’après ce qui précède,nous pouvons remplacer l’élément de masse par l’élément d’arc.

D’après un calcul déjà fait (cliquer ici pour voir) :  «   , par suite :

Nous savons déjà  (cliquer ici pour voir) que le dénominateur de cette « fraction »  a pour valeur « 8a ». Quant  au numérateur,on peut écrire :  

Pour calculer cette intégrale,posons : «  »  , on en déduit «    et  «  »  et  on en déduit l’intégrale : « 

Qui devient :   =    =

Par suite :  =    ou encore :    = 

Exemple n°2  :

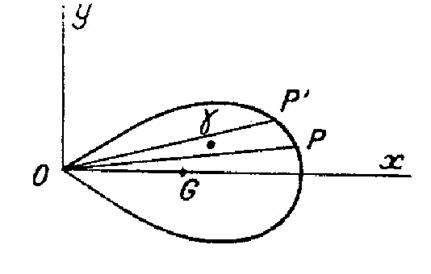
Trouver le centre de gravité de l’ aire d’une boucle de la lemniscate  «  ».

(voir figure ci contre).

Par symétrie ,le centre de gravité « G » se trouve sur l’axe « Ox ».Il suffit donc d’en chercher l’abscisse.

Décomposons l’aire en petits triangles tel que « POP ’ ».
Chacun d’eux peut être remplacé par un point matériel situé en son centre de gravité «  », c'est-à-dire aux deux tiers du rayon vecteur « 0P ».

Quant à la masse du point «  » c’est la surface «  »  du triangle « POP’ »

On a donc :   = 

Ces deux intégrales sont naturellement , étendues à l’aire de la lemniscate. Il revient au même de doubler le résultat obtenu en intégrant entre  « 0 »  et «  ».

On trouve ainsi :

  =    =  = 

et

  =

Pour calculer cette dernière intégrale , posons «  »  , d’où «  »  , de sorte que l’intégrale devient : 

Il ne reste plus qu’à faire disparaître l’exposant : «  » en posant « », d’où  »  ,  

On obtient ainsi :

Ce dernier calcul  est classique . On a :

Puis :

   =

Par suite l’intégrale devient :

ou

  =  

De là résulte que l’abscisse du centre de gravité est :

 =  =

Exemple III .

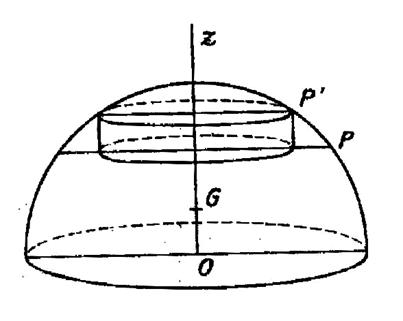
Calculer le centre de gravité du volume d’une demi -sphère de rayon « R ».

(voir la figure ci contre).

Décomposons  le volume de la demi – sphère en éléments infiniment petits, par des plans parallèles au plan de base.

L’un de ces éléments  peut être assimilé à un cylindre dont le centre «  » est à la base distance « z » du centre « O » de la demi – sphère . Le rayon de ce cylindre est : «  . Sa hauteur est  «  » .

Son volume est  «  »

Et c’est ce volume que nous prenons pour masse du point «  »

D’où la côte «  »  du centre de gravité  cherché :

Le dénominateur qu’il est inutile de calculer par une intégrale , est le volume «  » de la demi- sphère ; le numérateur a pour valeur :

 =   =

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!

EVALUATION :

calculer :

Reprendre chaque exercice du cours.

Voir le cours !!!!!