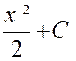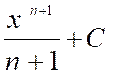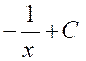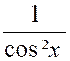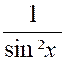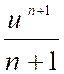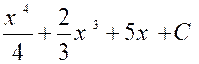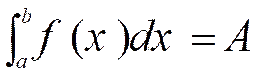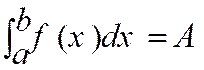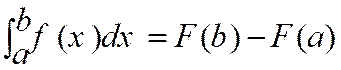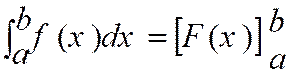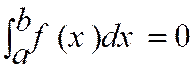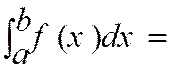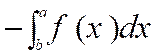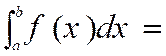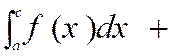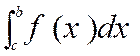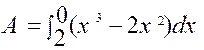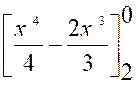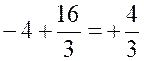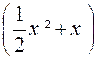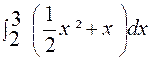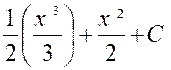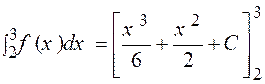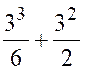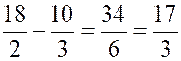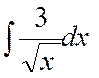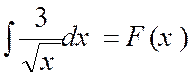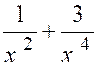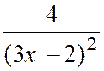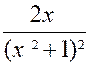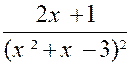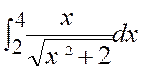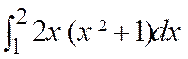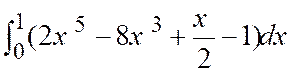Pré requis:
|
Info : liste des
connaissances en algèbre préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
AVANT :
|
APRES :
|
Complément
d’Info :
1°)
Liste des cours : prépa concours
A consulter pour
compléments : 4°) Suite :
Module sur les primitives et les
intégrales |
||
|
|
|
|
|
|
TITRE :PREPARATION CONCOURS niveau IV : Résumé de
cours sur : FONCTIONS « PRIMITIVE » ET « INTEGRALE »
|
|
- Primitive d’ une fonction . |
|
|
|
- Tableau
des primitives usuelles. |
|
|
|
- Intégrale d’une fonction . |
|
|
|
- Notations :
Intégrales et primitives |
|
|
|
- Propriétés : |
|
|
|
- Exemples |
|
Travaux auto – formatifs.;
devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
Résumé :
COURS
14 – Primitive d’ une fonction .
|
14.1 – Primitive d’ une fonction . |
|
|||||||
|
|
Soient « f » et « F » des fonctions définies
sur un intervalle [a ; b ]. On dit que
« F » est une primitive de « f » si et seulement
« F » est dérivable sur
[a ; b ]
et admet « f » pour dérivée. |
|
||||||
|
|
« F »
primitive de « f » sur [a ; b ] |
|
||||||
|
14.2 –
Tableau des primitives usuelles. |
||||||||
|
|
|
|||||||
|
|
|
Fonctions : f (x) |
Primitives :
F (x) |
|
|
|||
|
|
|
« a » (constante) |
a
x +C |
|
|
|||
|
|
|
x |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
x n |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
U’ + V’ |
U
+ V + C |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
a
u’ |
a
u + C |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|||||||
|
|
Exemple : F (x) = x² est
une primitive de « f » telle que
f (x) = 2 x Si F est une primitive de « f » , toute fonction primitive de « f » est
définie par ( F + C ) où C représente
une fonction constante.
F (x) = x3 ; G (x) = x3 -2 ; H (x) = x3 + 5 ;
U (x) = x3 + 10 sont des
primitives de : f(x) = 3 x² ; |
|
||||||
|
|
|
Fonctions : f (x) |
Primitives :
F (x) |
|
|
|
|
|
ex |
ex |
|
|
|
|
|
|
|
|
|
|
|
|
cos
x |
sin
x |
|
|
|
|
|
|
|
|
|
|
|
|
sin
x |
-
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
tan
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
-
cotan x |
|
|
|
|
|
|
|
|
|
|
|
|
u’v
+ u v’ |
uv |
|
|
|
|
|
u’
u n |
|
|
|
|
|
|
|
|
|
|
|
|
|
u’e u |
e u |
|
|
|
|
|
|
|
|
|
|
|
|
u’
cos u |
Sin u |
|
|
|
|
|
|
|
|
|
|
|
|
u’
sin u |
-
cos u |
|
|
|
|
|
|
|
|
|
|
Exemple : f(x) =
x 3 + 2 x² + 5
; F (x) = |
||||
|
15 –
Intégrale d’une fonction . |
||||
|
|
|
|||
|
|
|
|
Notation :
( lire :
somme
de a à b de f(x) dx ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15-
2 : Notations : Intégrales
et primitives : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 – 3
Propriétés : |
|
|
|
|
|
|
|
|
|
|
|
·
Bornes égales : |
|
|
|
|
|
|
|
|
|
|
|
·
Intervention des bornes : |
|
|
|
|
|
|
|
|
|
|
|
·
Relation de Chasles : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15
– 4 Exemples : |
|
|
|
|
|
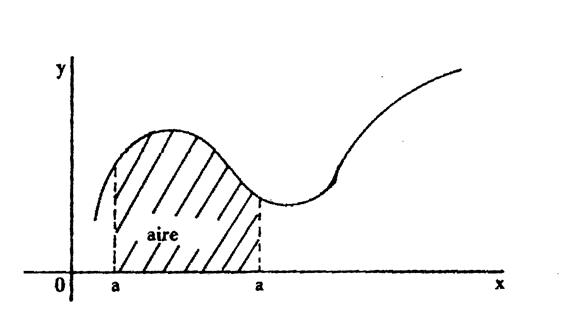
1°)
f(x) = x3 – 2 x²
Trouver l’aire ( A ) comprise
entre « a = 2 » et
« b =0 » |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2°) on pose
f’ (x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3°) |
|
|
|
|
|
|
|
|
|
|
|
4°) |
|
|
|
|
|
|
|
||
|
|
TRAVAUX AUTO FORMATIFS. |
||||
|
|
|
|
|||
|
|
CONTRÔLE |
|
|||
|
|
Voir le cours !!!!! |
|
|||
|
|
|
|
|||
|
|
EVALUATION :
|
|
|||
|
|
|
|
|||
|
|
Exercices : Calculer les primitives
. |
|
|||
|
|
|
|
|||
|
|
1°)
f (x) = 3 x² - 4x + 7 |
|
|||
|
|
|
|
|||
|
|
2°)
f (x) = 1 - |
|
|||
|
|
|
|
|||
|
|
3°)
f (x) = 4 ( x
-1) 4 |
|
|||
|
|
|
|
|||
|
|
4°)
f (x) = |
|
|||
|
|
|
|
|||
|
|
5°)
f (x) = x3 ( x4 +
1 ) ² |
|
|||
|
|
|
|
|||
|
|
6°)
f (x) = (3 x² +1 ) ( x 3 + x ) |
|
|||
|
|
|
|
|||
|
|
7°) f (x) = |
|
|||
|
|
|
|
|||
|
|
8°) f (x) = |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Exercices : Calculer les intégrales :. |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||