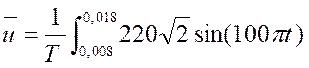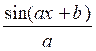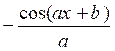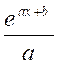Index « warmaths »

>> ( voir « cours d’algèbre) et + >>> liste des Cours niveau 4

>> Vers cours niveau 3 -2 (en cours) Suite : Module sur les primitives et les intégrales

Vers cours « calcul intégral » niveau 4

Résumé cours niveau IV- CALCUL INTEGRAL

Chapitres :

· PRIMITIVE D’UNE FONCTION

Le tableau des fonctions usuelles et de leurs primitives ; Exemples

· INTEGRALE D’UNE FONCTION SUR UN INTERVALLE

Exemple 

· SIGNIFICATION GRAPHIQUE DE L’INTEGRALE

· PROPRIETES DES INTEGRALES

· MOYENNE

· VALEUR EFFICACE

· EXERCICES D’APPLICATION

1. PRIMITIVE D’UNE FONCTION

La primitive F d’une fonction f définie sur un intervalle I de l’ensemble des nombres réels est telle que F’(x)=f(x)

Pour calculer une primitive d’une fonction f revient à faire l’inverse du calcul de la dérivée d’une fonction.

Exemples

Ø Comment calculer une primitive de la fonction g : x ® 2x ?

Lorsque l’on regarde le tableau des fonctions et de leurs dérivées on a :

Fonction f	Dérivée f’
x²	2x

Une primitive de la fonction g : x® 2x est telle que G’(x) = g(x)

Donc une primitive de g est G(x) = x² en effet G’(x) = 2x = g(x)

Pourquoi dit-on une primitive et non pas la primitive ?

Pour la fonction g : x® 2x la fonction G(x)=x²+3500 est aussi une primitive, d’une manière générale toutes les fonctions du type G(x)=x²+ k ( où k est un nombre réel ) sont des primitives.

Pour une fonction f donnée, il existe une infinité de primitive telle que F’(x) = f(x).

Ø Comment calculer une primitive de la fonction h  : x® x² ?

Lorsque l’on regarde le tableau des fonctions et de leurs dérivées on a :

Fonction f	Dérivée f’
x^3	3x²

Il faut lors du calcul de la primitive s’arranger pour que le facteur « 3 » disparaisse devant le x² on prend donc comme primitive de x² la fonction H(x)=

Vérifions en dérivant :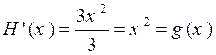

Le tableau des fonctions usuelles et de leurs primitives est :

fonction f(x)	Primitive F(x)
x^n	+C
cos(x)	sin(x)+C
sin(x)	-cos(x)+C
cos(ax+b)	+C
sin(ax+b)	+C
	Ln(x)+C
	+C

La primitive d’une somme de fonctions est égle à la somme des primitives des fonctions

La primitive d’une fonction multipliée par une constante est égale à la primitive de cette fonction multipliée par la constante.

Exemples

· Primitive de ®

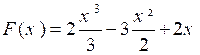
· Primitive de ®

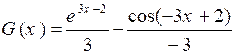
FExercice n°1

Calculer les primitives des fonctions suivantes :

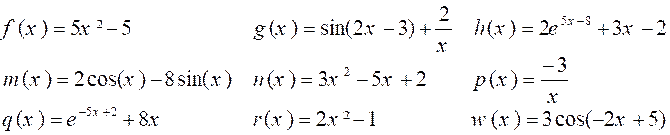
2. INTEGRALE D’UNE FONCTION SUR UN INTERVALLE

Par définition l’intégrale I d’une fonction f sur l’intervalle [a ; b] de primitive F est le nombre :

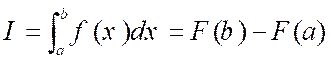
NB : On note également

Exemple : Comment calculer ?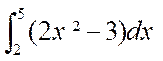

Il faut déjà déterminer une primitive de la fonction 2x²-3. Cette primitive F est :

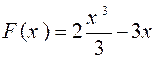
D’après la définition :

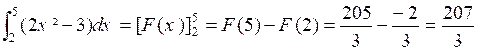
FExercice n°2

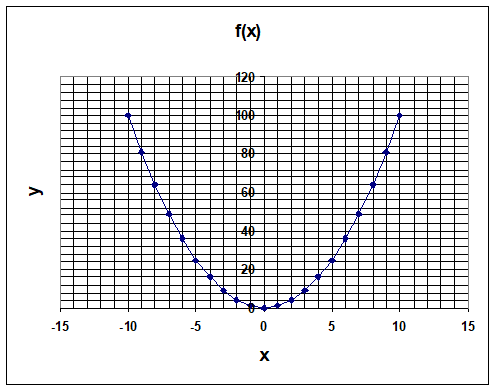
Calculer les intégrales suivantes :

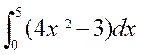
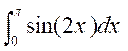
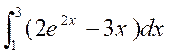
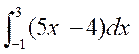
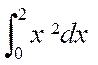
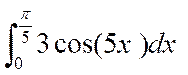
3. SIGNIFICATION GRAPHIQUE DE L’INTEGRALE

Pour illustrer cette partie, nous allons nous intéresser à la fonction f(x)=x², la représentation graphique de cette fonction est une parabole ( voir ci-contre).

Calculons 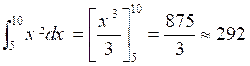à l’unité près

Calculons maintenant l’aire située en dessous de la courbe de f comprise entre x = 5 et x =10. Pour cela nous allons 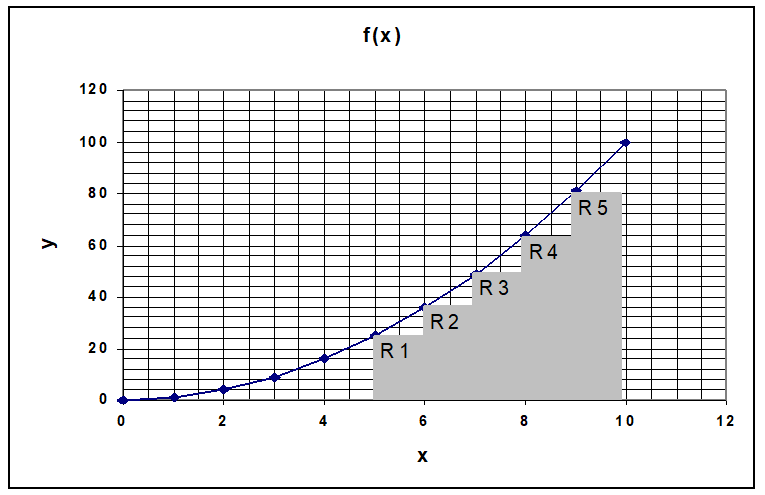utiliser une méthode approchée dite des rectangles :

On va assimiler l’aire totale de la courbe à la somme des aires des rectangles R1, R2, R3, R4 et R5.

L’aire d’un rectangle est A=L´l

Dans notre cas :

………

L’aire totale est donc :

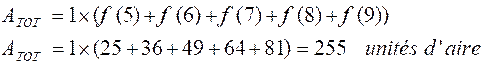
Si on recommençait ce calcul avec des rectangle de largeur 0,01 on aurait :

à l’unité près

On constate donc que

D’une manière générale, graphiquement l’intégrale d’une fonction positive entre x₁ et x₂ est égale à l’aire de la courbe située entre l’axe des abscisses et les droites d’équations x=x₁ et x=x₂ .

4. PROPRIETES DES INTEGRALES

Ces propriétés découlent des propriétés opératoires des fonctions dérivées :

Linéarité : 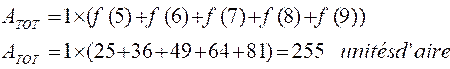où k est un nombre réel.

Relation de Chasles :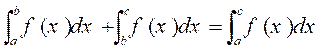

5. MOYENNE

La valeur moyenne, notée , d’une fonction f, sur un intervalle [ a ; b] est donnée par la relation :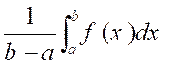

6. VALEUR EFFICACE

La valeur efficace d’une fonction f sur un intervalle [ a ; b ] est notée F_eff et est donnée par la relation :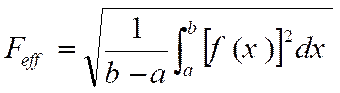

7. EXERCICES D’APPLICATION

1°) Un sèche linge est alimenté par une tension u en fonction du temps donnée par la relation :

Où la tension est exprimée en volts et le temps en secondes

Calculer la valeur moyenne de u sur l’intervalle [0 ; 0,01]

2°) Dans le cas d’une tension alternative sinusoïdale u telle que u(t)=U_maxsin(wt) calculer U_eff.

Rappel : La période T de cette tension est donnée par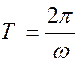 

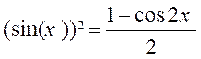
3°) Calculer l’aire délimitée par la courbe représentative de la fonction f(x)=3x²-5x+2 et les droites d’équations x=2 et x=4.

4°) Calculer les intégrales suivantes :

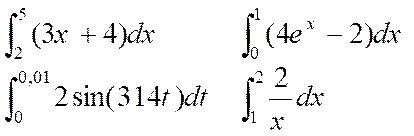
5°)Un circuit comprenant un générateur de force contre électromotrice E=18 V, une bobine de résistance R=12 W et d’inductance L=0,24 H. La fermeture à l’instant t=0 provoque l’installation d’un régime transitoire. Dans cette phase, l’intensité du courant i(t) à l’instant t est donné par l relation :

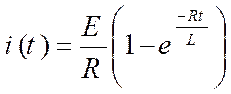
i est exprimée en ampères et t en secondes

5.1°) Montrer que

5.2°) Déterminer la dérivée i’ de la fonction i. Etudier le sens de variation de la fonction i sur l’intervalle [0 ; 0,1]

5.3°) Compléter le tableau suivant :

t(s)	0	0,01	0,02	0,03	0 ,04	0,05	0,08	0,1
i(A) arrondi au millième

5.4°) Tracer la courbe C représentative de la fonction i dans un repère orthogonal d’unités graphiques : 1 cm pour 0,01 s en abscisses et 1cm pour 0,1 A en ordonnée

5.5°) Déterminer graphiquement le temps t₁ tel que l’intensité soit 0,75 A

5.6°) Calculer la quantité d’électricité Q exprimée en coulombs, mise en jeu entre les temps 0 et 0,1. on rappelle que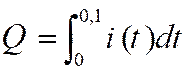

6°) La figure ci-dessous est l’oscillogramme obtenu aux bornes d’un onduleur :

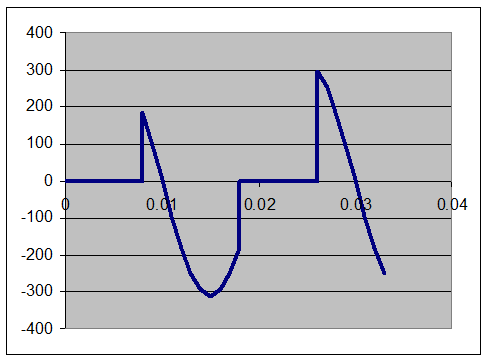
6.1°) Quelle est la période T du signal observé

6.2°) En déduire la pulsation w

6.3°) La fonction de base étant la fonction u définie par

Calculer la valeur moyenne du signal soit