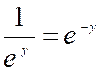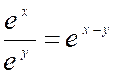Pré requis:
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif suivant |
|
||
|
|
|
||
|
|
|
|
|
DOSSIER
: LA FONCTION
EXPONENTIELLE
|
1 ) Résumé : |
|||||||
|
|
Définition |
||||||
|
|
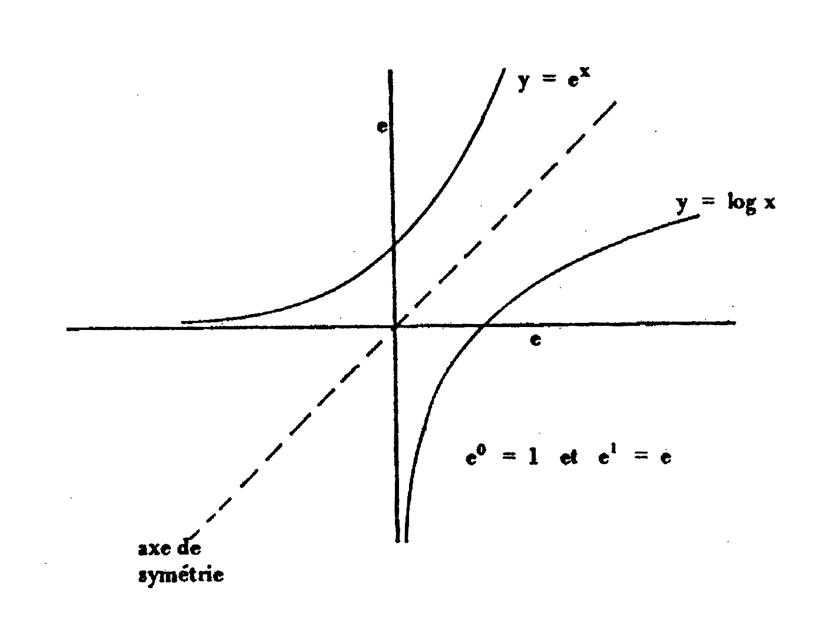
Représentation graphique de la fonction : y = e x |
||||||
|
|
Relations fondamentales. |
||||||
|
|
Exercices : Résoudre . |
||||||
|
|
|
||||||
|
|
|
Travaux
auto formatifs |
|
|
Corrigé
des Travaux auto formatifs |
||
|
TEST |
Interdisciplinarité : |
|
|||||
|
|
|
|
|
|
|
|
|
Nous
avons déterminer
des puissances de la forme y = a x. La base « a » peut
être un nombre quelconque.
Dans le cas particulier où a = e =
2,71828 nous aurons y= e x=
2,71828
« e » est la base
des logarithmes naturels appelés encore logarithmes népériens.
RESUME DU
COURS :
|
|
Définition :
On appelle « fonction exponentielle de base « e » la
fonction réciproque de la fonction « log ». On note ex l’image de « x » par cette
fonction. |
|
||||
|
|
Représentation graphique de la fonction : e x |
|||||
|
|
|
Domaine de définition : (Df) Df = ]
- Lim. ex = - x Lim. ex =
+
x |
||||
|
|
On appelle donc , une
fonction exponentielle , une fonction de la
forme : y = a x |
|
||||
|
|
Dans laquelle « a » est un nombre
positif fixe et « x » une variable pouvant prendre des valeurs de - |
|||||
|
|
C’est la première fois que nous rencontrons ainsi
la variable « x » en exposant. C’est l’étude des logarithmes qui
conduit à la considération de cette fonction que nous examinons ; nous
supposons que « x » peut prendre des valeurs positives ou négatives très voisines les unes des autres mais
toujours commensurables |
|||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
||||||
|
|
Relations fondamentales. |
Exemples : Résoudre : |
||||
|
|
ex ey
= e x+ y |
a) Log x = 8 |
|
|||
|
|
|
b) 5 + 6
Log x = 3 |
|
|||
|
|
|
|
|
|||
|
|
(ex
) n = exn |
|
|
|||
|
|
|
|||||
|
|
Remarques |
Dérivée. |
||||
|
|
Si y = ex |
|
||||
|
|
|
y = ex ;
y ‘ = ex |
||||
|
|
Log e x = x |
|
||||
|
|
|
y = e u ;
y ‘ = e u . u
’ |
||||
|
|
e log x = x |
|
||||
|
|
|
|
||||
Info
+calcul de la valeur « e »
++
|
|
y
= ex |
Exemple:
Calculer e 0,1
et e 10
e 2
= 2,71 828 2 = 7,4
e 0,2
= 2,71828 0,2 = 1,2216
Les fonctions exponentielles y = e
x ont une grande importance en Physique. De nombreux phénomènes
naturels comme l'échauffement et le refroidissement d'un corps, la charge et la
décharge d'un circuit électrique, la transformation radio active, sont régis
par ces fonctions.
Si on donne une expression du
genre y = e f (x) et si on nous demande de
déterminer les valeurs de y correspondant à différentes valeurs de x,
nous conseillons de calculer d'abord les valeurs f(x1),
f(x2), f(x3) ... correspondant
aux différentes valeurs x1, x2, x3
... et de les juxtaposer dans un tableau de valeurs. C'est
ensuite seulement qu'on déterminera e f (x) en
déplaçant simplement le curseur de la règle.
|
|
|
||
|
TRAVAUX AUTO FORMATIFS. |
|
||
|
|
|
|
|
|
|
CONTRÖLE : |
|
|
|
|
|
|
|
|
|
Voir le résumé ci-dessus |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exercices : Résoudre . |
|
|
|
|
|
|
|
|
1.
|
Log x =
8 |
|
|
|
|
|
|
|
|
2.
|
5 + 6
Log x = 3 |
|
|
|
|
|
|
|