FONCTIONS LOGARITHMES ET EXPONENTIELLES

Index warmaths		Les fonctions logarithmes népériens et exponentielles s

		Liste des cours disponibles sur les logarithmes.
		Les fonctions exponentielles.

Cours niveau 4 (bac prof..) sur les fonctions logarithmes et les fonctions exponentielles

Liste des cours disponibles sur les logarithmes.

I- LES FONCTIONS LOGARITHMES .

I.1. Fonction logarithme népérien

I.2. Fonction logarithme DECIMAL

I.3. UTILISATION DES FONCTIONS LOGARITHMES

II- LES FONCTIONS EXPONENTIELLES

II.1. FONCTION EXPONENTIELLE DE BASE « e »

II.2. FONCTIONS EXPONENTIELLES DE BASE « a »

Nota : Si besoin, voir le cours sur les fonctions numériques pour les questions de vocabulaire.

Les corrigés des exercices du cours sont donnés à la fin du document.

I. FONCTIONS LOGARITHMES

I.1. Fonction logarithme népérien

¬ Définition

La fonction logarithme népérien notée "Ln" est la fonction qui a tout nombre x fait correspondre le nombre Ln(x) = Ln x.

Cette fonction n'est définie que pour x > 0.

Cette fonction s'annule pour x = 1 soit : Ln 1 = 0.

Pour calculer le logarithme népérien d'un nombre, il faut utiliser la touche Ln de votre calculatrice. Suivant le modèle deux modes de fonctionnement existent :

Exemple : On veut calculer le logarithme népérien de 2 soit Ln 2

+Exercice n°1

A l'aide de votre calculatrice donnez les valeurs des logarithmes népériens des nombres suivants (quand cela est possible) Arrondir les résultats à 0,001 près.

x	12	15,5	-8	3,14	87	100000	3669,778	1475	0
Ln x

Propriétés opératoires

Pour tout nombre a et b strictement positifs on a :

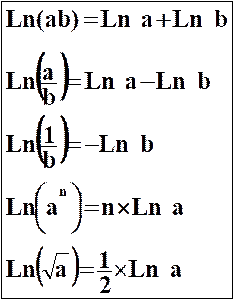
Ainsi, la fonction Logarithme népérien, transforme une multiplication en une addition et une division en une soustraction.

+Exercice n°2

En utilisant les propriétés opératoires de la fonction Ln, exprimer en fonction de Ln (a) et Ln (b) les nombres suivants :

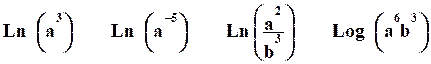
® Définition du nombre e

Le nombre e est tel que Ln e = 1. Sa valeur est e » 2,718281828…….

Pour avoir la valeur de e à l'aide de votre calculatrice il faut procéder à la séquence de touches suivantes :

+Exercice n°3

En utilisant les propriétés opératoires de Ln et celle du nombre e calculer

¯ Représentation graphique de la fonction Ln

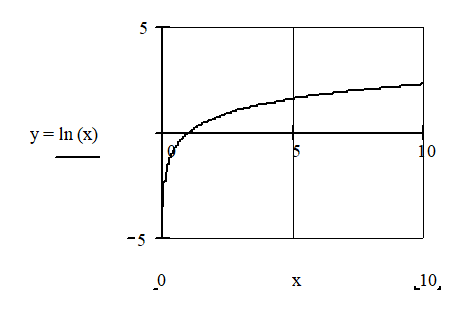
La représentation graphique de la fonction Ln, constitué des points de coordonnées (x ; y=Ln x ).

Elle passe par le point de coordonnées ( 1 ; 0 ) , puisque Ln 1 = 0.

Elle passe également par le point de coordonnées ( e ; 1 ) puisque Ln e = 1.

Quand x devient très grand ( valeurs positives) alors Ln x devient très grand également. On dit que Ln x tend vers plus l'infini (on note + ∞) quand x tend vers plus l'infini ( On note - ∞).

Quand x devient très petit, (il s'approche de plus en plus de zéro ) , Ln x devient très grand dans les valeurs négatives : On dit que Ln x tend vers moins l'infini (on note - ∞ ) quand x tend vers zéro ( car Ln 0 n'existe pas )

Le tableau de variation de cette fonction est :

Valeurs de x	0 + ∞
Sens de variation de Ln x

On met une double barre en dessous du zéro pour montrer que la fonction Ln n'est pas définie pour x = 0.

La fonction Ln est une fonction strictement croissante donc :

Si a = b alors Ln(a) = Ln (b)

Si a >b alors Ln (a) > Ln (b)

Si a < b alors Ln (a) < Ln (b)

I.2. Fonction logarithme DECIMAL

¬ Définition

Elle est définie à partir de la fonction Ln par : 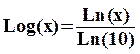pour x > 0

Pour calculer la valeur du logarithme décimal d'un nombre, on utilise la touche Log de la calculatrice. Le principe de fonctionnement est le même que pour la fonction Ln.

Propriétés opératoires

Les propriétés opératoires sont les mêmes que la fonction Ln.

Deux propriétés supplémentaires qui découlent de la définition sont : Log (10) = 1 et Log ( 10^x ) = x

En eff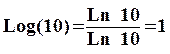et : et car Log 10 = 1.

+Exercice n°4

Sans utiliser votre calculatrice, compléter le tableau suivant :

x	10²	10^-5	10⁸	10^-5,7	10^-12,7	10⁹⁹	10^-37,5	10³	10¹
Log x

® Représentation graphique de la fonction Log

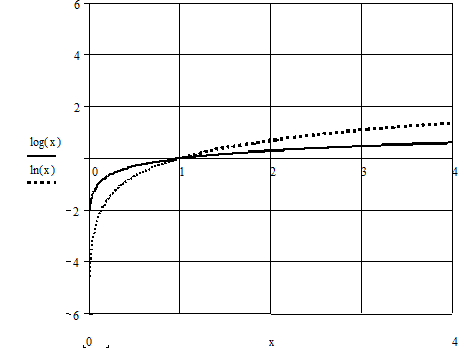Puisque Ln 10 > 0, Le tableau de variation de la fonction Log est le même que celui de la fonction Ln.

La courbe représentative est similaire.

La fonction Log est une fonction croissante. Sur ce graphique sont tracées les deux représentations graphiques des deux fonctions.

De plus on remarque que :

Pour x > 1, Log (x ) > 0 et Ln (x) > 0

Pour x < 1, Log (x) < 0 et Ln(x) < 0

Le tableau de variation de la fonction Log est :

Valeurs de x	0 + ∞
Sens de variation de Log x

I.3. UTILISATION DES FONCTIONS LOGARITHMES

On utilise ces fonctions pour résoudre des équations dans lesquelles l'inconnue est un exposant.

Exemple La valeur acquise C_n d'un capital C placé à intérêts composés au taux t annuel pendant n années est donné par la relation :

C_n = C (1 + t )ⁿ

On veut déterminer au bout de combien d'années n la valeur acquise C_n un capital de 29 400 € placé à 6 % vaudra 40 000 €.

La première étape consiste à remplacer dans la relation donnée les grandeurs que l'on connaît :

A savoir C = 29 400 € t = 0,06 C_n = 40 000 €

La relation devient avec ces valeurs :

40 000 = 29 400 ( 1 + 0,06 )ⁿ

40 000 = 29 400 ´ 1,06ⁿ

On veut déterminer la valeur de n, il faut donc dans un premier temps isoler dans le membre de droite 1,06ⁿ en divisant les deux membres de l'équation par 29 400 :

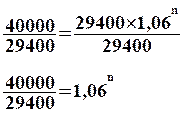
C'est à partir de cette équation que l'on va se servir des propriétés opératoires des fonctions logarithmes.

On prend le logarithme décimal ( ou népérien peut importe car elles ont les mêmes propriétés opératoires) des deux membres :

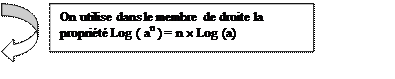
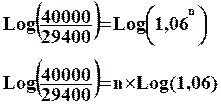
On peut maintenant diviser les deux membres de l'équation par Log(1,06) afin d'isoler n et d'en déterminer ainsi la valeur.

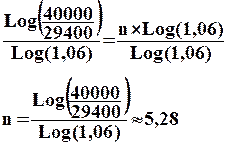
Il faut donc environ 5,28 années soit 5 ans et 3 mois et 11 jours environs.

+Exercice n°5

Un capital de 2 500 € est placé à intérêts composés au taux annuel de 5 %.

1°) Calculer la valeur acquise par le capital au bout de 4 ans.

2°) Calculer le nombre d'année de placement nécessaires pour obtenir une valeur acquise de 4 275,85 €.

+Exercice n°6

A l'aide de votre calculatrice, calculez complétez le tableau suivant ( Arrondir à 0,001 près )

x	-3,5	8	-1/2	3/4	6	0
e^x

Propriétés opératoires

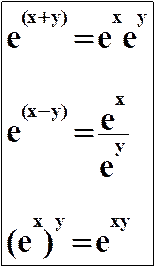Quels que soient les nombres x et y on a :

L'exponentielle transforme une somme en produit.

Elle transforme une différence en quotient.

Une propriété importante est que les fonctions Logarithme népérien et exponentielle sont des fonctions réciproques

Leurs effets sur un nombre x "s'annulent" mutuellement.

En effet : e^ln³ = 3 Ln (e³) = 3

D'une manière plus générale pour tout nombre x : Ln (e^x ) = x et si x > 0 e^Ln^(x) = x

® Représentation graphique

La représentation graphique de la focntion exponentielle est constituée des points de coordonnées ( x ; y = e^x)

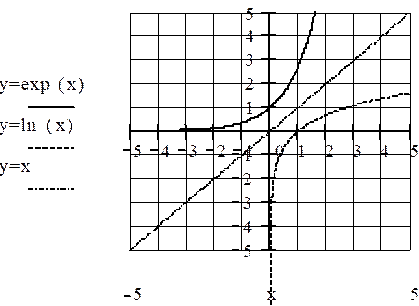La réciprocité des deux fonctions logarithmes népérien et exponentielle impliquer une symétrie par rapport à la première bissectrice (droite d'équation y = x ) des courbes représentatives des deux fonctions :

La fonction exponentielle est également une fonction croissante.

Lorsque x devient très grand ( on dit qu'il tend vers + ∞ ), e^x devient très grand également ( e^x tend vers + ∞).

Lorsque x tend vers des valeurs négatives très grandes, e^x devient nulle. On dit que lorsque x tend vers -∞ alors e^x tend vers zéro.

Des constatations précédentes on peut établir le tableau de variations suivant :

Valeurs de x	- ∞ + ∞
Sens de variation de e^x

Puisque la fonction exponentielle est une fonction croissante on a donc les propriétés suivantes :

Si x = y alors e^x = e^y

Si x > y alors e^x > e^y

Si x < y alors e^x < e^y

II.2. FONCTIONS EXPONENTIELLES DE BASE « a »

¬ Définition

On appelle fonction exponentielle de base a (a > 0 et différent de 1), la fonction qui a x fait correspondre a^x. Elle est définie pour tout nombre x.

Exemple la fonction exponentielle de base 3 est définie par 3^x.

Pour calculer 3^x pour x = 1,5 on utilise la touche puissance de la calculatrice (en général notée y^x)

Ainsi 3^1,5 = 5,196152…….

Propriétés opératoires

Mais pourquoi dit-on "fonction exponentielle de base a" ? En effet, derrière le a^x se "cache" une exponentielle :

Posons : y = a^x de façon à avoir une égalité.

Prenons les logarithmes népériens des deux membres de l'égalité précédente :

Ln(y) = Ln (a^x)

En utilisant dans le membre de droite une propriété opératoire de Ln on a :

Ln(y) = x ´ Ln (a)

Prenons l'exponentielle de chaque membre :

e^Ln⁽^y) = e^x^´^Ln(a)

Or e^Ln^(y)= y, l'égalité devient : y = e^x^´^Ln(a)

Or au départ on a posé y = a^x donc a^x = e^x^´^Ln(a)

Il faut donc retenir que :

a^x = e^x^´^Ln(a)

C'est la raison pour laquelle on dit que a^x est une fonction exponentielle de base « a » .

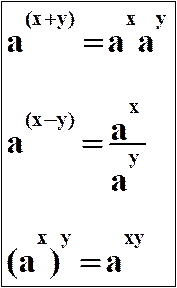Les propriétés opératoires sont les mêmes que pour les exponentielles de base « e » :

+Exercice n°7

Résolvez les équations suivantes :

3 ^x = 2 4 ^x = 5 2 ^x = 3 2 ^x+1 = 3

Indication : il faut prendre le logarithme de chaque membre et utiliser les propriétés opératoires des logarithmes.

Les corrigés des exercices du cours sont donnés cliquez ici :.