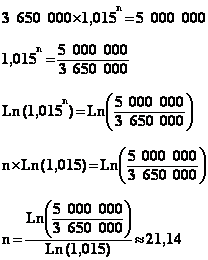CORRECTION DES EXERCICES SUR LES LOGARITHMES ET EXPONENTIELLES

Exercice n°1

1°) En 1999 : 1 an après : 3 650 000 ´ 1,015 = 3 704 750

En 2000 : 2 ans après : 3 650 000 ´ 1,015´1,015 = 3 650 000 ´ 1,015² = 3 760 321,25

On remarque qu'à ce stade, la population d'une année sur l'autre constitue les termes d'une suite géométrique de raison 1,015 et de premier terme 3 650 000.

En 2003 : 5 ans après : 3 650 000 ´ 1,015⁵ = 3 932 086,61 ( au centième )

En 2008 : 10 ans après : 3 650 000 ´ 1,015¹⁰ = 4 235 974,01 ( au centième)

En 2028 : 20 après : 3 650 000 ´ 1,015²⁰ = 4 916 020,77 ( au centième)

2°) D'après la question 1°) On a : P_n = 3 650 000 ´ 1,015ⁿ

3°) La courbe représentative de cette fonction est constitué des points de coordonnées ( x ; 3 650 000 ´ 1,015^x ) pour x allant de 0 à 30 :

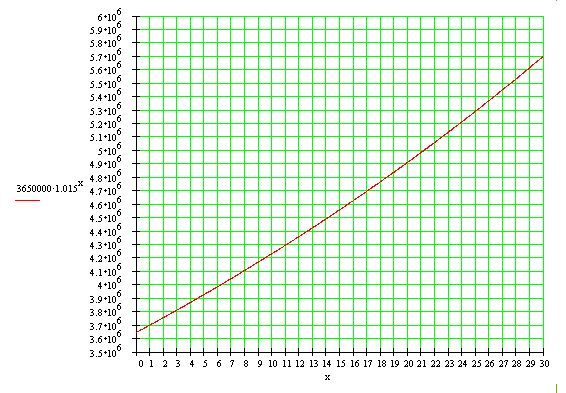
4°) D'après le graphique, il faut un peu plus que 21 ans.

5°) Il faut donc chercher pour quelle valeur de n on a P_n = 5 000 000 . On doit alors résoudre l'équation d'inconnue n telle que :

3 650 000 ´ 1,015ⁿ = 5 000 000

La résolution est va nécessiter l'emploi de la fonction Ln pour pouvoir déterminer n. Mais il faut d'abord isoler 1,015ⁿ :

Les étapes de la résolution de cette équation sont les suivantes :

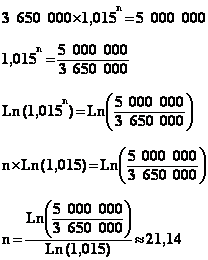
Ce résultat confirme la prévision graphique.

Exercice n°2

1°) la machine se déprécie de 20 % par an ce qui signifie qu'elle garde 80 % de sa valeur d'une année sur l'autre. La valeur de la machine d'une année est donc égale au produit de 0,8 par la valeur de la machine l'année précédente donc :

V₀ = 9 000 €

V₁ = 0,8 ´ 9 000 =7 200 €

V₂ = 0,8 ´ V₁ = 0,8 ´ 0,8 ´ 9 000 = 0,8² ´ 9 000 = 5 760 €

V₃ = 0,8 ´ V₂ = 0,8 ´ 0,8² ´ 9 000 = 0,8³ ´ 9 000 = 4 608 €

2°) Pour passer d'une valeur à la suivante on multiplie par 0,8 donc les valeurs seront les termes d'une suite géométrique de raison 0,8 et de premier terme V₀ = 9 000.

On a alors : V_n = V₀ ´ 0,8ⁿ

3°) n = 0 : V₀ = V₀ ´ 0,8⁰ = V₀ = 9 000 €

n = 1 : V₁ = V₀ ´ 0,8¹ = V₀ ´ 0,8 = 9 000 ´ 0,8 = 7 200 €

n = 2 : V₂ = V₀ ´ 0,8² = 9 000 ´ 0,8² = 5 760 €

Au bout de huit ans de fonctionnement : n = 8 : V₈ = V₀ ´ 0,8⁸ = 9 000 ´ 0,8 = 1509,94944 €

4°) a) Lorsque x croit, f(x) décroît donc la fonction f est décroissante.

4°) b)

4°) c)

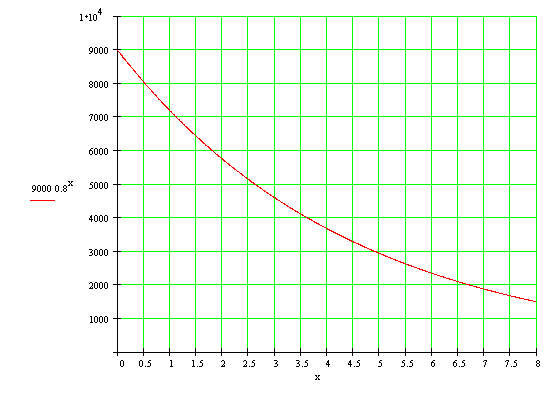
5°)a) on veut : ¦(x) = 4 000 : Il donc faut chercher sur le graphique l'abscisse x du point qui a pour ordonnée 4000 , sur le graphique on lit environ 3,6.

5°)b) il faut donc résoudre l'équation : 9 000 ´ 0,8^x = 4 000

Les étapes de cette résolution sont :

A l'aide de la résolution de l'équation on trouve x = 3,63.

Exercice n°3

1°) Le pourcentage d'augmentation peut se calculer de la façon suivante :

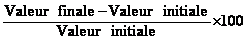
Pour 1993-1994 :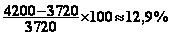

Vérification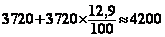

De la même façon pour 1994-1995 : 27,4 % 1995-1996 : 12,1 % 1996-1997 : 21,7 %

1997-1998 : 11,6 %

2°) Il faut résoudre l'équation en t : 9 850 = 3 720´(1+t)⁶

Les étapes de résolution sont les suivantes :

Le taux annuel moyen d'augmentation entre 1993 et 1999 est donc de 17,62 %

Vérification : 3 720 ´ ( 1+ 0,1762 )⁶ ≈ 9 850 .

Si on prend le sixième du pourcentage d'augmentation entre 1993 et 1999 on trouve : 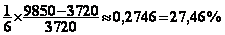cela suppose ici que l'on a une variation affine du taux de variation en fonction du nombre d'année alors que celle-ci est plutôt exponentielle (voir question 3°))

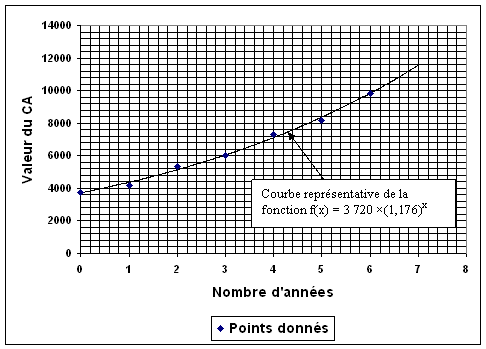3°)

On constate que la fonction donnée s'ajuste bien sur les points donnés.

Exercice n°4

1°) a)Ln(x) est une fonction croissante donc -Ln(x) est une fonction décroissante alors ¦(x) est décroissante.

1°) b) Le tableau de variation de ¦ est donc :

¦(0,2) = - 8 310´Ln(0,2) ≈ 13 374 ¦(1) = - 8310´Ln(1) = 0

Valeurs de x	0,2 1
Sens de variation de ¦	13 374 0

1°) c)

x	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
f(x)	13400	10000	7600	5800	4200	3000	1900	900	0

1°) d)

2°) a)

¦(0,25) = - 8310´Ln(0,25) ≈ 11 500

Le fossile a donc 11500 ans

2°) b) il faut trouver l'abscisse du point sur la courbe ayant pour ordonnée 11 500

ce point a pour abscisse

x = 0,25

Exercice n°5

1°) Si ce bien se déprécie de 20 % par an, alors il garde 80% de sa valeur d'une année sur l'autre alors :

P₂ = 0,8´P₁ = 0,8´20 600 = 16 480

P₃ = 0,8´P₂ = 0,8´0,8´20 600 = 0,8²´20 600 = 13 184

P₄ = 0,8´P₃ = 0,8³ ´ 20 600 = 10 547,2

2°) Pour Passer d'un nombre à l'autre on multiplie par 0,8. Ces nombres sont donc les termes d'une suite géométrique de raison 0,8 et de premier terme P₁ = 20 600.

3°) D'après la formule qui permet de calculer le terme de rang n on a :

P_n = 0,8ⁿ´P₁=20 600´0,8ⁿ

4°) a) Calculons

¦(0) = 20 600´0,8⁰ = 20 600 = P₁

¦(1) = 20 600´0,8¹ = 16 480 = P₂ ect ……..

Voir tableau ci après.

4°) b) D'après le tableau ci-dessus, lorsque x croît ¦(x) décroît donc ¦ est décroissante.

4°) c) Voir graphique

4°) d) Il faut lire sur la courbe, l'abscisse du point dont l'ordonnée vaut 11 700. On lit x ≈ 2,6

x	0	1	2	3	4	5
¦(x)	20 600	16 480	13 184	10 547,2	8437,8	6750,2

5°)