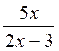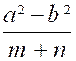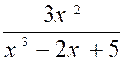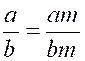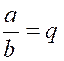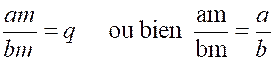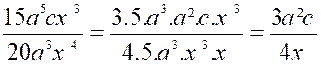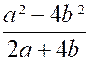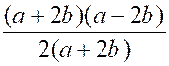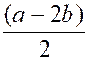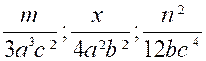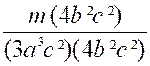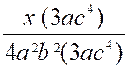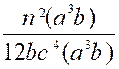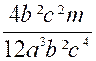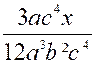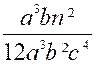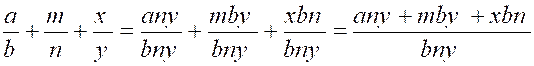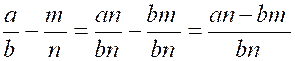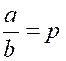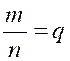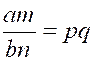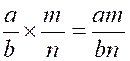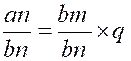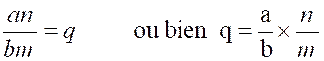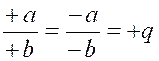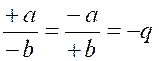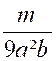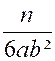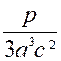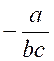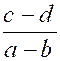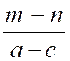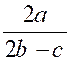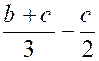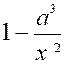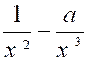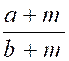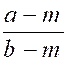Pré requis
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier :
|
Objectif
précédent : |
Objectif suivant : |
|
||
|
INFORMATIONS : Tout sur "la
fraction" et "les écritures fractionnaires……." |
||||
|
|
|
|
|
||||
|
TEST |
COURS
|
|
|||||
COURS n° 1
RAPPELS :
Rappel 1: toute expression algébrique
qui n’est pas exactement divisible par une autre , a comme quotient de la division une
fraction algébrique.(voir division des nombres algébriques)
Définition ;
Une fraction algébrique exprime toujours le quotient de son numérateur par son dénominateur .
Cela
indique la division entre deux expressions algébriques .
Toutes
les propriétés des fractions arithmétiques sont également vraies lorsqu’il
s’agit de fractions algébriques.
Activité
annexe , avec la calculatrice , mais importante:
On veut montrer ce qui se passe lorsque l’on divise
le nombre 1 (soit le plus petit nombre ) par un nombre inférieur à 1( 0
,........1.) et qui tend
vers zéro.(plus le chiffre « 1 »
recul plus le nombre tend vers zéro.)
Utiliser
la calculatrice pour calculer :
1 divisé par
1 = ; noter le résultat ;..............................................................
1 divisé par 0.1 = ; noter le résultat
;.................................................................
1 divisé par 0.01= ;
noter le résultat ;...............................................................
1
divisé par 0.001= ; noter le résultat ;
.............................................................
1
divisé par 0.000001 =
; noter le
résultat;......................................................
;
Après
avoir noté le résultat .de chaque opération on peut conclure « que plus un nombre est divisé
par un autre qui tend vers zéro ,plus le
résultat devient grand
.On dira que le résultat tendra vers un
nombre infiniment grand (en valeur absolue)
on doit conclure : on ne peut donc diviser par « zéro ».
D'où
Lorsqu'une écriture fractionnaire contient une lettre au
dénominateur ('appelée :inconnue ; généralement
"x"" ) il faut
trouver la valeur de "x" qui
doit être exclue , afin de ne pas
avoir la valeur zéro:
Exemples:
|
Soit les écritures
fractionnaires suivantes : |
commentaire |
|
|
Pour
effectuer un calcul
;il faut donner une valeur à "x", toutes les valeurs
sont possibles sauf "0" |
|
|
Pour
effectuer un calcul
;il faut donner une valeur à "x", toutes les valeurs
sont possible sauf "0" ; 2 fois 0 = 0 Zéro
est l 'élément
absorbant : |
|
|
Un
calcul est possible sauf si x+1 = 0 ; Il
faut calculer (résoudre)pour connaître quelle est la valeur de "x" qui donne "_"+1 =0 On
trouve x = -1 ;
si x=-1 ;alors (-1) +1 =0 Conclusion:
un calcul est possible avec toutes les valeurs de "x" sauf "x = -1" |
|
|
Est
exclue la valeur de "x = 1,5" |
|
|
(il
y en a trois) Attention :
« a » doit être différent de zéro.
|
|
COURS n° 2 Fractions
algébriques (suite)
|
|
On donne le nom de fraction algébrique ou fraction littérale à l'indication
entre deux monômes ou polynômes, d'une division qui en général
ne peut s'effectuer exactement ; telles sont les
expressions
Tous les
principes et toutes les règles que nous avons
développés en arithmétique sur les fractions numériques sont applicables aux
fractions littérales et reposent sur
cette même proposition fondamentale : que l'on peut toujours multiplier ou diviser les deux
termes d'une fraction par une même quantité sans
altérer la valeur de celte fraction, c'est-à-dire qu'on a toujours l'égalité En effet, en
représentant par q le quotient, quel qu'il soit, ou la valeur de la fraction En multipliant les deux membres de cette dernière égalité par la même
quantité m, elle ne sera nullement détruite et donnera am = bq m
ou am = bm x q, d'où l'on tire, en divisant par bm,
On déduit de ce principe la simplification
des fractions algébriques, ainsi que la réduction de plusieurs fractions au môme dénominateur. Simplification. Elle consiste à débarrasser les deux termes d'une fraction de tous les facteurs qui leur
sont communs. Ainsi, on aura
par la suppression de 5a3x3. (facteurs communs au numérateur et dénominateur) De même , |
|
|
Réduction au même dénominateur |
|
|
|
|
On effectuera cette réduction en
multipliant en général les deux termes de chaque fraction par le produit des dénominateurs de toutes les autres ;
mais ici, comme en arithmétique, il ne
faut pas négliger le cas où des facteurs communs aux divers dénominateurs permettraient d'obtenir un dénominateur commun plus' simple en prenant le
plus petit multiple. Alors le
dénominateur commun à plusieurs fractions
se composera de tous les facteurs gui entrent dans les
dénominateurs des fractions données, pris une seule fois, mais avec l'exposant h plus élevé. Ainsi, par exemple, soit à réduire au même dénominateur les fractions suivantes :
Pour former le plus petit multiple qui soit divisible par
chacun des trois dénominateurs ci-dessus, nous prendrons
tous les facteurs différents que contiennent ces dénominateurs, lesquels sont
3, 4, a, b, c, et nous leur donnerons l'exposant
qu'ils ont dans le terme où cet exposant est le plus élevé
pour chacun d'eux, ce qui fournira le produit suivant pour le
dénominateur commun aux fractions proposées : 3 x 4 x a3 x b3 x c1
= 12 a3b² c4 Maintenant,
pour effectuer la réduction demandée, il suffira de multiplier les deux
termes de chaque fraction par le quotient qui existe entre le
dénominateur commun 12 a3b² c4
et son dénominateur propre, c'est-à-dire qu'on multipliera les deux termes de
la première fraction par 4 b² c² ( pour devenir la fraction équivalente : Alors les fractions proposées deviendront : |
|
|
ADDITION DE FRACTIONS : |
|
|
|
|
Règle : Pour
ajouter (additionner) plusieurs fractions entre elles, il faut les réduire d'abord au même dénominateur, faire ensuite la somme des numérateurs et donner à cette somme le dénominateur commun ; ainsi :
|
|
|
SOUSTRACTION
DE FRACTIONS : |
|
|
|
|
La soustraction ne peut
s'opérer sur les numérateurs qu'après toutefois que les deux fractions ont été réduites au même dénominateur ; on aura donc
|
|
|
|
|
|
|
MULTIPLICATION
DE FRACTIONS : |
|
|
|
|
On fait le produit de plusieurs fractions en multipliant les
numérateurs entre eux et les dénominateurs entre eux. Soient les deux
fractions ce qui donne a = bp et
m = nq Mais si les deux quantités
a
et m sont respectivement égales aux deux
autres bp et nq, le produit , des deux premières égalera aussi le
produit des deux autres, et l'on
aura : a x m = bp
x nq,
ce qui revient à am = bn x pq
; et enfin, en divisant par la .quantité bn, on
aura :
|
|
|
|
|
|
|
DIVISION
DE FRACTIONS : |
|
|
|
|
On effectue la division d'une fraction par une autre en multipliant
la fraction dividende par la fraction diviseur
renversée, Soit à diviser les deux fractions Ou bien ( en multipliant à gauche
et à droite ; les deux membres par
En réduisant au même
dénominateur, on tire de là : <ft
supprimant le dénominateur commun bn, on
ne troublera pas l'égalité, et l'on
aura : an = bm
x q ; * enfin, en divisant de
part et d'antre par bm, cette dernière égalité
donne :
ce qui prouve la règle énoncée. Remarque. Dans les démonstrations
ci-dessus nous avons admis que les deux termes des fractions proposées
étaient positifs ; mais, s'il en était autrement, la règle
n'en serait pas moins vraie, Il est important de rappeler à cette
occasion que la valeur absolue d'une fraction algébrique est indépendante
des signes de ses termes, et que, de plus, cette valeur
est positive si les deux termes ont le même signe, et
négative s'ils ont des signes contraires, c'est-à-dire qu'on
aura, dans la division algébrique (chapitre :
règle des signes),
ce qui prouve que l'on peut changer les signes des deux termes d'une fraction sans altérer sa valeur. |
|