Le tracé d’un parallélogramme sans contrainte de dimensions (angle et longueurs des segments) ne pose pas de problème particulier. On trace deux droites parallèles puis une droite sécante à ces deux droites puis une droite parallèle à cette troisième droite.

► Identifier un parallélogramme :

Remarque : on nomme un parallélogramme par des lettres majuscules. Par convention, ces lettres sont lues dans le sens des aiguilles d’une montre, le premier point nommé est celui qui se trouve le plus en haut à gauche de la figure.

Exemples :

pa5

Parallélogramme (ABCD)

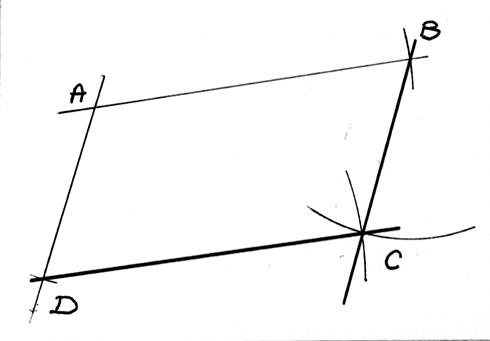
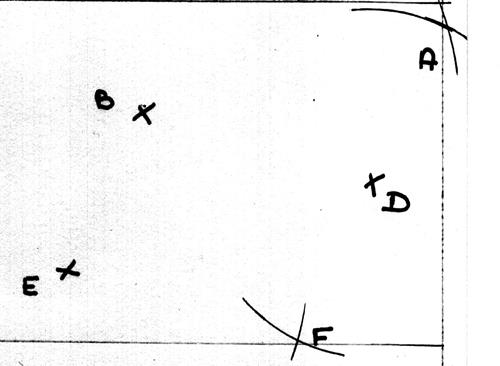
paraexo1co

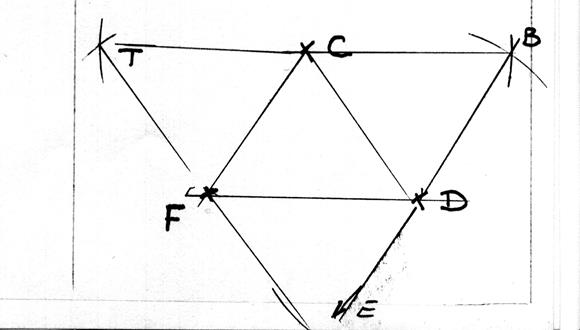
Dans la figure ci contre je peut identifier le parallélogramme (BADE)

et le parallélogramme (BDFE)

( joindre les points pour constater que nous avons bien deux parallélogramme.)

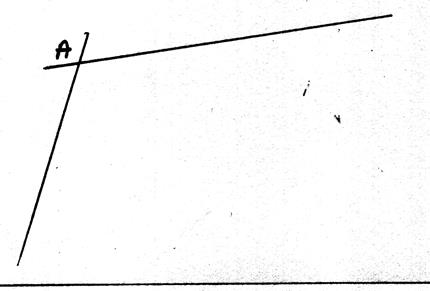
► 1 - CONSTRUCTION d’ un parallélogramme à partir d’une droite et un point « O » extérieur à la droite

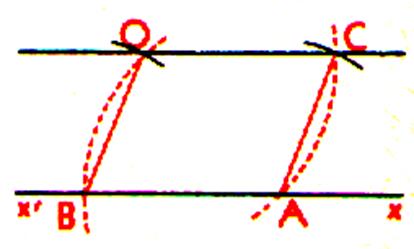
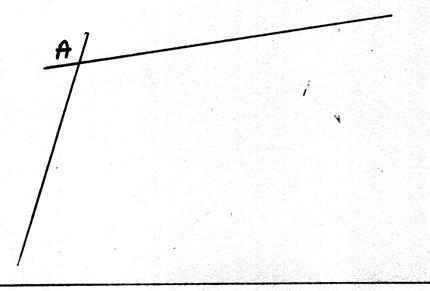
Du point « O » comme centre , avec un rayon plus grand que la distance de ce point à la droite x’x , on trace un arc de cercle qui coupe cette droite au point A.

Du point A comme centre , et avec le même rayon que précédemment , on trace un second arc de cercle qui passe par « O » et qui coupe la droite x’x au point B.

Du point A comme centre , avec un rayon égal au segment OB , on trace un troisième arc , qui coupe le premier en C :

La droite OC est parallèle à la droite x’x . En effet : le quadrilatère convexe ABOC est parallélogramme car il a ses cotés opposés égaux deux à deux :

On a OA = OC ; OA =BA donc OC = AB

et OB = AC

donc AB et OC sont parallèles

paraconst

Voir d’autres tracés :

Recherche du quatrième sommet d’un parallélogramme avec un compas.

►à partir de deux droites sécantes.

►à partir de trois points.

Ces types de tracés vont être utiles lorsque l’on cherchera à tracer un bipoint équipollent à un bipoint donné.

Pour comprendre la définition d’un vecteur et la translation d’un vecteur dans un plan. En vue de faire la somme de plusieurs vecteurs.

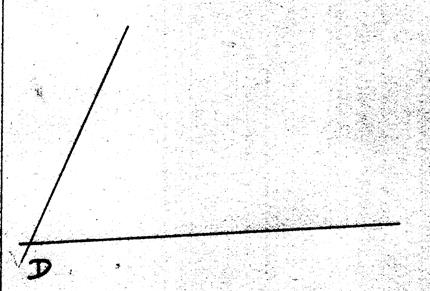
► 2 - CONSTRUCTION d’ un parallélogramme à partir de deux droites sécantes .

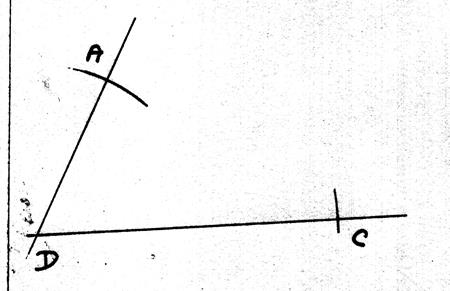
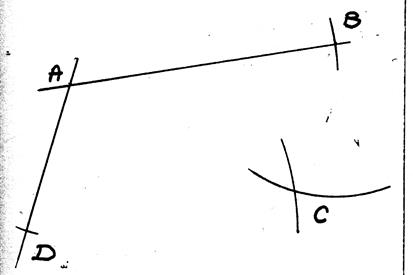
A ) ACTIVITE : On va tracer le parallélogramme (ABCD) en partant du point « D ».

1°) on trace deux droites sécantes : on obtient un point « D »	2°) on place deux points « A » et « B »

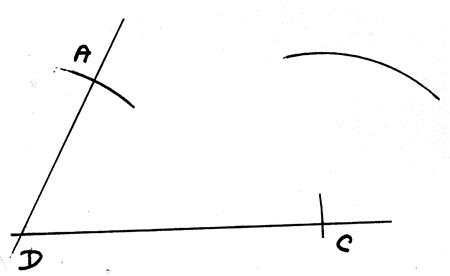
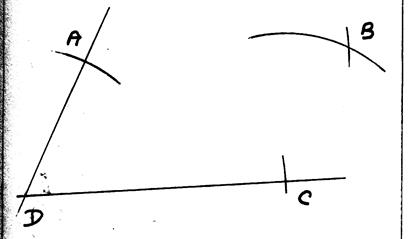
3°) avec le compas on relève la distance DA puis on trace un arc de cercle ce centre « C »	4°) avec le compas on relève la distance DC puis on trace un arc de cercle ce centre « A » , on obtient le point « B »

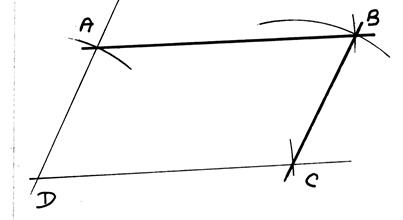
On a tracé le parallélogramme (ABCD)

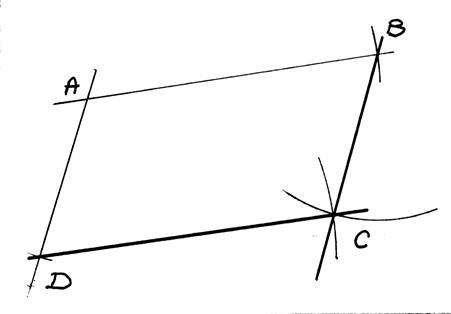
B ) ACTIVITE : On va tracer le parallélogramme (ABCD) en partant du point « A ».

1°) On trace les droites sécantes. On place le point « A »	2°)On place les points « B » et « D »

3°) On trace le premier arc de cercle , rayon AD de centre « B »	4°) On trace le second arc de cercle de rayon AB de centre « D ».

On trace le parallélogramme( ABCD)

► 3 - CONSTRUCTION d’ un parallélogramme à partir de trois points.

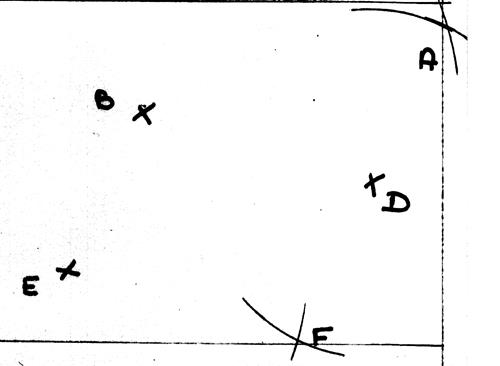
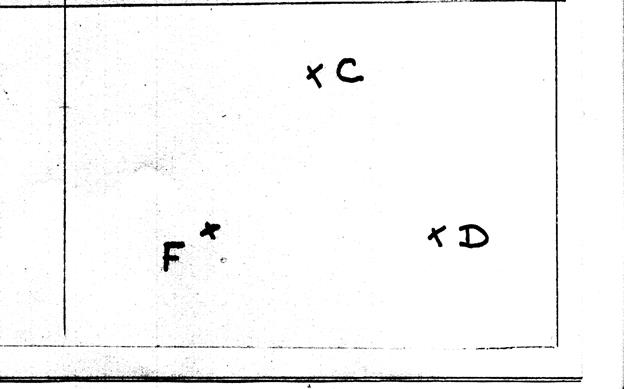
On veut tracer le parallélogramme( BADE) et ensuite le parallélogramme (BDFE)

Tracer le parallélogramme( BADE)
On veut tracer le parallélogramme( BADE) : On doit « imaginer » où doit se trouver le point « A ». · il est entre « B » et « D » en haut à droite. On trace un arc de cercle de rayon EB de centre « D » et un arc de rayon ED et de centre « B ». Autrement : On trace un arc de cercle de rayon ED de centre « B » et un arc de rayon BE et de centre « B ».
Tracer le parallélogramme( BDFE)
On doit « imaginer » où doit se trouver le point « F ». · il est entre « D » et « E » en haut à droite. On trace un arc de cercle de rayon BD de centre « E » et un arc de rayon BE et de centre « D ». Autrement : On trace un arc de cercle de rayon DB de centre « E » et un arc de rayon EB et de centre « D ».

TRAVAUX AUTO- FORMATIFS.

CONTROLE :

(6^ème) 1 ) Donner la définition d’un parallélogramme :

(5^ème) 2 ) Citer les trois principales propriétés d’un parallélogramme.

EVALUATION

Série 1 :

Tracer un parallélogramme ABCD

pa1

Tracer un parallélogramme ABCD

pb1

Tracer un parallélogramme BACD

Tracer le parallélogramme : BDFE

Tracer les parallélogrammes

CBDF ;

CDEF ;

TCDF

Série 2 :

1°) construire un parallélogramme , sachant que deux côtés consécutifs mesurent respectivement 3 cm et 5 cm et que l’angle compris entre ces deux côtés mesure 54°.

Calculer les autres angles de ce parallélogramme .

2°) construire sans rapporteur un parallélogramme , sachant que ses deux diagonales mesurent respectivement 7 cm et 5 cm et forment entre elles un angle de 120°.

3°)Construire un parallélogramme dont les côtés mesurent respectivement 5,5 cm et 3,5 cm et la hauteur 2 cm.

4°) Construire sans rapporteur un parallélogramme , sachant que le côtés AB mesure 6 cm , la diagonale AC 8 cm et que l’angle BAC est égal à 30°.

5° ) Construire un parallélogramme ABCD , sachant que le côté AB mesure 3 cm , le côté BC 5 cm et la diagonale AC 7 cm.

Autres :

Parallélogramme ABCD de côtés AB = 35 mm et AD = 45 mm et = 120°
Parallélogramme ABCD tel que AB = 26 mm et AD = 48 mm et la diagonale BD = 40 mm
Parallélogramme ABCD de côté AB = 5cm et de diagonales AC = 4 cm et BD = 80 mm
Parallélogramme ABCD tel que AB = 2,5cm et AD = 5cm et la diagonale AC = 64 mm
Parallélogramme ABCD de côtés AB = 5cm et AD = 4cm et de hauteur AH = 3cm
Parallélogramme ABCD de côté AB= 30 mm et de hauteurs AH = 25 mm et AK = 32 mm ( niveau +++)

CORRIGE :

Tracés : BADC et BDFE

paraexo1co

Remarquez ces tracés particuliers.

paraexo3Co