CORRIGE DES FICHES SUR ……

Classe de 5^ème de collège

Retour vers les fiches ….

Programme de la classe de 5^ème

FICHE 1 : Somme des angles dans : Le Triangle quelconque. ( dit aussi « scalène » ) .

FICHE 2 : Somme des angles dans : Triangle rectangle.

FICHE 3 : Exercices types sur la somme des angles d’un triangle

FICHE 4 : Somme des angles dans : Triangle isocèle .

Cas : le triangle rectangle isocèle ; cas : le triangle équilatéral.

FICHE 5 : Triangle ayant deux angles égaux.

FICHE 6 : Somme des angles d’un quadrilatère non – croisé.

FICHE  7 : l’ HEXAGONE régulier.

FICHE 1 : Le Triangle quelconque. ( dit aussi « scalène » )

(voir cours @ P6)

Mesurez les angles de triangle « DEF » puis faites la somme de ces angles.

    +     +   = ……° + ……….° + ……...°= ………..°

On peut alors se poser  les questions suivantes :

1°) Cette somme  est-elle exactement de 180° ? …………

 2°) Est-il de même pour tous les triangles ?.............

Pour répondre à ces questions , nous allons faire le raisonnement suivant :

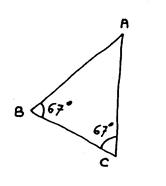
« ABC » est un triangle quelconque.

Tracez par « A »  la parallèle à ( BC ).

Appelons « xy » cette droite.

On pense aux angles déterminés par ces droites et une sécante.

Les angles ci-dessous sont dits : « alterne- interne »

Les angles ci-dessous sont dits : « alterne- interne »

Ces angles sont donc ……………égaux………………..

On peut affirmer que    =     et       =   

La somme des angles  du triangle « ABC » est :   +    +

Elle est donc la même  que :      +   +       soit :           +    +     

Or     +    +       =     =  180 °     , donc    +  +   = 180 °

Le raisonnement que l’on vient de faire ne dépend pas de la forme du triangle, on peut donc dire :

A retenir :

Dans tout triangle , la somme des angles est égale à ………….180°…………….

Activité n° 1…..

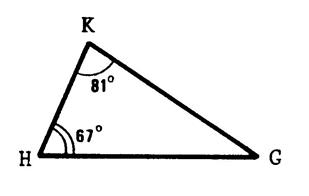
« GHK » est un triangle tel que    = 67°  ,   = 81°, nous pouvons calculer l’angle  .

Puisque la somme des angles d’un triangle est égale à 180° ;

Alors    +  +   = 180°

C'est-à-dire    + …67°…..°   + …81°….°  = …180..°  , alors     + …148°….°  = …180..° 

Donc :    + …148°…-  148°   = …180..°  - 148 °   ,  ( voir le cours sur les transformations d’égalité)

soit    + 0°   = …180..°  - 148°  ,  ( voir le cours sur les transformations d’égalité)

ou   = …180..°  - 148° =  32°  

résultat :    =   32°  

Activité n° 2 …..

Soit « LMN » un triangle tel que  = 20 °       et     = 35°

Calculez  et construisez un tel triangle.

FICHE 2 : Somme des angles dans : Triangle rectangle.

La figure « ABC » ci- contre est un triangle rectangle en « A ».

Cela signifie que l’angle    = …90°….

Donc    +    = 180°- …90°…=  90°..

Donc    +     sont « aigus » .

Et par suite      < …90°… ;et     < …90°…..

Donc      et     ont  …« complémentaire ».

……………

Sur la figure  placez le point « C »

A retenir :

Dans un triangle rectangle les angles autres que l’angle droit sont aigus  et complémentaires .

Activité 1

Dans un triangle « ABC »  ci- contre ,

     =  65°

Calculez l’angle   .

(25°)

Activité 2

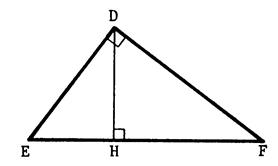
Soit le triangle rectangle « DEF »  rectangle en « D »

[ DH] est sa hauteur .

Marquez sur la figure , les angles égaux ( oral : expliquez brièvement ).

Sachant que   = 36°  , calculez les angles :

 ,  ,

FICHE 3 : Exercices types sur la somme des angles d’un triangle.

Activité 1

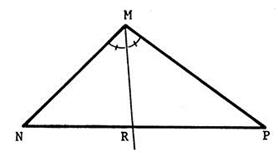
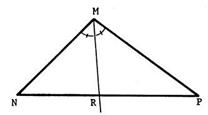
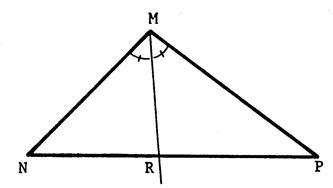
Soit un triangle « MNP » tel que  = 98° et  = 36°

La demi droite [ MR  est la bissectrice de l’angle .

Calculez :   ;   et 

Activité 2

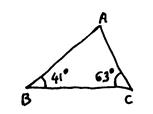
Dessinez ( en taille plus grande) un triangle « ABC » représenté ci-contre grossièrement .

Ci-contre , le côté « [ BC ] » est déjà placé.

 = 63° ,  = 41 °.

Tracez la hauteur [ A H ]

Tracez la bissectrice  [ A E )  de 

Calculez les angles suivants :

 ,  ,  ,  ,

Activité 3

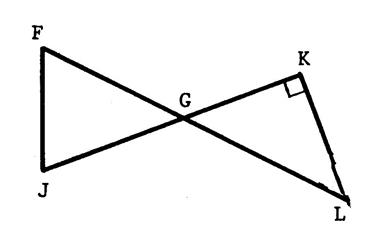
Sur la figure ci- contre  « GKL » est un triangle rectangle.

 = 63°   ;   = 70 °  .

Calculez     .

FICHE 4 : Somme des angles dans : Triangle isocèle .

Info : @ le triangle isocèle.

Rappels :

·       On appelle « triangle isocèle » tout triangle ayant au moins deux côtés de même …longueur…..

Ces angles sont appelés « angles à la base »du triangle isocèle.

·       Tous triangle isocèle admet un axe de symétrie qui est la …….bissectrice…..de sa base. Tracez-la.

·       La hauteur principale , la médiane principale, la médiatrice principale et la bissectrice principale ont leur support confondu avec l’axe de symétrie.

Activité n° 1

Soit un triangle « KLM »  isocèle de base [ L M ] ( ci-contre)

 = 108 °.

Calculez   et  .

Activité n° 2

« EFG » est un triangle  isocèle de base [ EG] .

 = 78°

1°) Calculez les autres angles du triangle.

2°) Tracez la médiane [ FH]  et calculez      et    

Activité n° 3

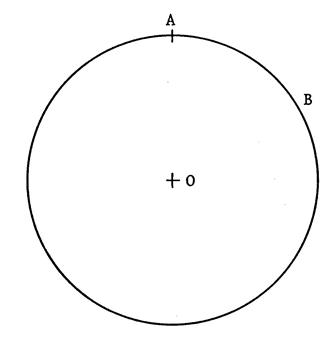
Ci-contre .

Voici un cercle de centre « O » .

[ BC]  est un diamètre.

1°) Sachant que  = 28° , calculez les angles suivants :

 ;  ;  ,  ,  ,

2°)   étant un angle aigu quelconque.

Pensez vous que l’on trouve toujours la même valeur pour  ? ( oral : expliquez !!!!!!)

Cas : le triangle rectangle isocèle :

Info @ le triangle rectangle @..

Voici , ci-contre, un triangle rectangle isocèle.

Calculez la valeur de ses angles aigus.

Cas : le triangle équilatéral :

Info @  sur le triangle équilatèral….

Un triangle équilatéral  est un triangle dont les trois côtés ont la même longueur.

Il peut donc être considéré comme un triangle isocèle  de …3 …façons différentes.

Ces trois angles sont donc …égaux…

Ils valent :   180 °    3  =  60 °

A retenir :

Dans tout triangle équilatéral , chacun des trois angles est égal à ..60 ° ….

FICHE 5 : Triangle ayant deux angles égaux.

Activité :

Dessinez ( en plus grand) un triangle « ABC »  représenté grossièrement , ci-contre.

Le côté [BC]   est placé ci-contre .

 et   = 67°

En apparence , que pouvez-vous dire du triangle « ABC » ?

……………………………………………………………..

C’est ce que nous allons prouver par un raisonnement .

1°) Tracez la hauteur | AH ].

Calculez       et    . Que pouvez-vous en déduire  pour  [ AH   ?

2°) Dans la symétrie  d’axe  ( AH ) ,

1°) Quelle est la symétrie de la demi-droite  [ AB  ?.................................

Expliquez pourquoi oralement…

2°) Quelle est la symétrie de la  droite  ( BC )  ? ………………………….

Expliquez pourquoi oralement…

3°) Quel est le symétrique du point « B » ?.................................

Expliquez pourquoi oralement…

4°) Quel est le symétrique du segment [ AB ] ? ………………………..

Expliquez pourquoi oralement…

5°) Vous en déduisez alors que AB   = ……….

Expliquez pourquoi oralement…

6°) Ce qui permet d’affirmer que « ABC » est un triangle ……………………………

Expliquez pourquoi oralement…

En faisant le même genre de raisonnement , on pourrait prouver que :

A retenir :

Tout triangle ayant deux angles égaux est un triangle …..isocèle…………..

C’est un nouveau procédé permettant de reconnaître qu’un triangle est isocèle.

En voici encore un autre procédé . ( Vous ferez la démonstration  verbalement )

Activité 1.

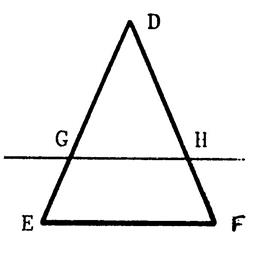
Ci-contre : « DEF » est un triangle isocèle de base [ EF ].

Une parallèle à (EF) coupe les côtés en « G » et « H ».

Prouvez que « DGH » est un triangle isocèle.

Démonstration :

( GH) est parallèle à ( EF ),

-        en considérant la sécante (DE)   ,   et  ……………..sont correspondants , donc   =

-        en considérant la sécante (DF)   ,   et  ……………..sont correspondants , donc   =

Puisque « DEF » est un triangle isocèle  alors   =    donc   = 

Ayant deux angles égaux  , le triangle DGH est donc isocèle.

Activité 2.

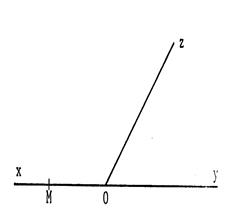
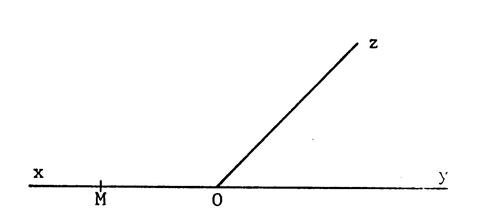
« O » et « M » sont des points de la droite « xy ».

[ Oz    est une demi-droite quelconque.

Tracez la bissectrice [ Ot     de   

Tracez par « M » la parallèle au support  de  [ Ot     .

Elle coupe [ Oz    en « N ». Pouvez que « OM = ON »   

Indication :

Prouvez que « OMN » est isocèle , pour cela trouvez des angles égaux.
Pensez  aux parallèles coupées par des sécantes.

FICHE 6 : Somme des angles d’un quadrilatère non – croisé.

Info @ le quadrilatère.

Concave.

Convexe

Croisé

Ci-dessus vous avez deux quadrilatères : l’un concave et l’autre convexe.

Ils sont non - croisés.

Activité :

Tracez la diagonale [AC] .

Vous déterminez ainsi deux triangles : « CDA » et « ABC ».

Conclusion :

La somme des angles du quadrilatère est égale à la somme des angles des 2 triangles.

A retenir :

La somme des angles d’un quadrilatère non-croisé est égale à …..360°……

FICHE  7  l’ HEXAGONE régulier.

Info @ plus sur l’hexagone.

Un hexagone régulier est un polygone qui a …… côtés de même longueur.

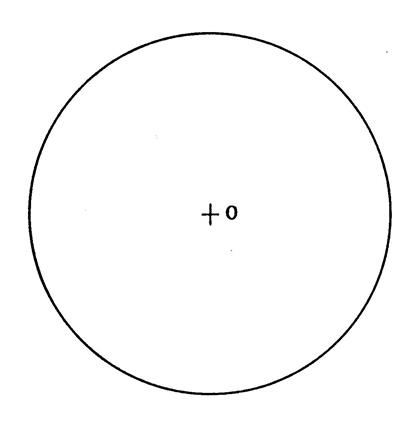
Et dont les sommets sont situés sur le cercle dont le rayon est égal à la longueur des côtés.

Activité :

On vous demande de construire l’hexagone régulier inscrit dans le cercle ci-contre ;

·       Partant du point « A » , en reportant le rayon, déterminez les autres sommets « B », »C », »D », »E », »F » et tracez les côtés de ce polygone.

·       Tracez : (OA) , (OB),(OC), ( OD ), ( OE ), ( OF )

Ø Puisque OA = OB = OC = le rayon, alors le triangle « OAB » est : …équilatéral……

Donc   = ….°  ,  = ……..° ;   = ……..°

Il en est de même pour    ,   ,   etc……

Ø Calculez     ,                =…………………..

Vous en déduisez que « A », « O » , « D »  sont …………………………………………………….. ;

Expliquez ( à l’oral) pourquoi  [ AD ]  ,  [ BE] ,   [CF ] sont des diamètres.

Ø Calculer l’angle :    …………………………………………………………………

Ø Calculez la somme des angles de l’hexagone régulier…………………………………

FICHE 8 : L’octogone régulier.

Info @ sur l’octogone

Un octogone régulier est un polygone  quia ………….côtés.

Ces côtés sont de même longueur et dont les sommets sont situés sur le cercle.

Ø On vous demande de construire l’octogone régulier inscrit dans le cercle  ci-contre.

Pour cela , tracez « 2 » diamètres perpendiculaires puis tracez les bissectrice des quatre angles que vous venez de déterminer.

Ces « 8 » demi-droites d’origine « O » coupent le cercle en « 8 » points , « A » , « B » , « C » , « D » , « E » , « F » , « G » , « H ».

Tracez les côtés de cet octogone.

Ø [ OB     est la bissectrice de    donc  = …….°

Ø Expliquez ( à l’oral si possible) pourquoi « AOB » est un triangle isocèle.

Ø Calculez   et   . …………………………………………………………………….

Ø Calculez  de même pour   ,    etc………………………

Ø Calculez    . …………………………………………………………………………………….

Ø Calculez la somme des angles de l’octogone régulier. ……………………………………………………………………

FICHE 9 : Une façon de prouver que des droites sont parallèles.

Info @ sur les parallèles.

Vous avez vu dans une leçon «  les angles « fiche 6 » )que :

si deux droites sont parallèles , elles déterminent avec toute sécante des angles correspondants égaux.

Inversement : on peut se poser le problème suivant :

Si deux droites déterminent avec une sécante des angles correspondants égaux, ces deux droites sont-elles parallèles ?

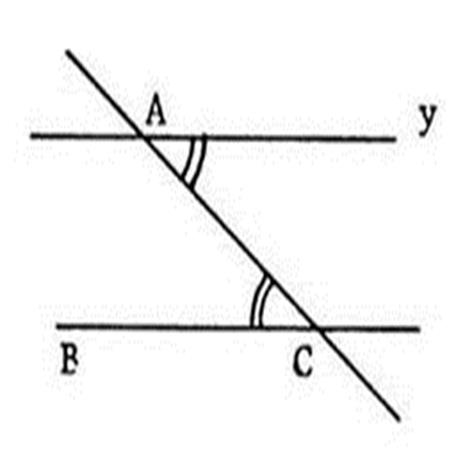
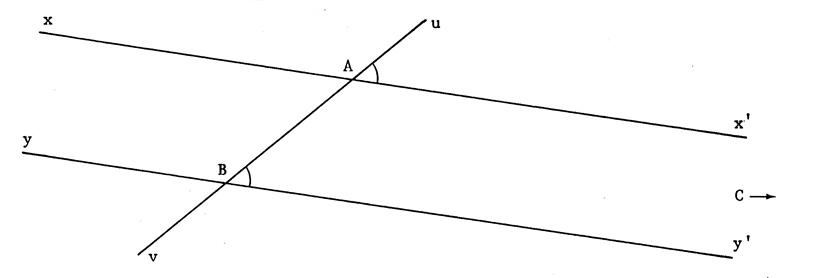
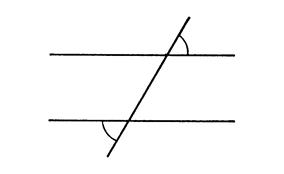
Voici , ci-dessous ,   deux droites  « xx’ »  et « y y’ » et une sécante « uv » qui les coupe en « A » et « B ».

   et    sont égaux . « xx’ »   et « yy’ » sont-elles parallèles ?

Expliquez pourquoi  (oralement si possible)          et    sont supplémentaires.

Puisque       et      sont égaux, alors    et      sont ………………supplémentaires…………………………..

Vous savez que , pour deux droites d’un plan , deux situations ( et deux seulement) sont possibles :

«  ou ces deux droites sont parallèles  ou elles sont  ………..sécantes……………. ».

Supposons que « xx’ »   et « yy’ » soient sécantes. Appelons « C » leur point d’intersection.

On aurait alors un triangle « ABC » dans lequel deux angles auraient pour somme « 180° » .

(     et      sont supplémentaires Ce qui est impossible.

Donc les droites « xx’ »   et « yy’ » ne peuvent être sécantes , elles sont donc …….. .parallèles …………

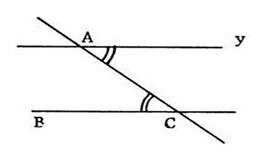
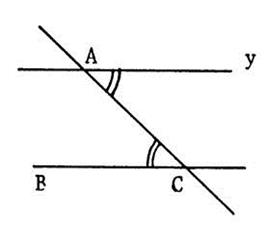
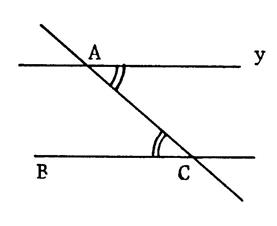
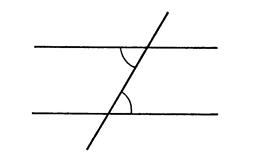
Dans les situations ci-dessous où les angles sont marqués par un arc de cercle sont égaux .

On eput affirmer que les droites sont parallèles .

Expliquez pourquoi ( à l’oral ,si possible ).

A retenir :

Si deux droites déterminent avec une sécante :

-        ou des angles alternes internes égaux

-        ou des angles alternes externes égaux

-        ou des angles correspondants égaux

alors ces droites sont parallèles.

Application :

Info : @ les tracés de parallèles.

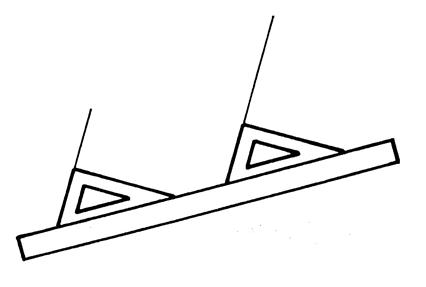
Vous comprenez alors pourquoi  on peut tracer des parallèles en utilisant une équerre et une règle

Le bord de la règle matérialise  la sécante et les deux positions de l’équerre matérialisent des angles …………..

Le 13/02/14