Géométrie : DOSSIER : les tracés géométriques II / Objectif cours 24a

Programme mathématiques classe 6^ème

Pré requis:

Classes élémentaires ( primaire)
b) Tracé d’un triangle quelconque
c) Voir tracé du triangle équilatéral
d) Tracé du triangle isocèle
e) Tracé du triangle rectangle
Les triangles (caractéristiques )

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : retour sur les triangles quelconques en 6^ème Triangles caractéristiques

Objectif suivant : Les triangles . suite : les triangles

tableau Tout sur les informations triangles

DOSSIER : LES TRACES des TRIANGLES

Classe de sixième : apprendre à identifier et construire des triangles
	1°) Rappels : le triangle en primaire.
	2°) Triangles quelconques : construction d’un…
	3°) Construction d’un triangle isocèle…
	4°) Construction d’un triangle équilatéral…
	5°) Construction d’un triangle rectangle …
	6°) Construction d’un triangle rectangle isocèle…
TEST		COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
					Travaux …les triangles et ……..

COURS

1°) Les triangles.
Nous avons déjà rencontré des triangles à l’école élémentaire.
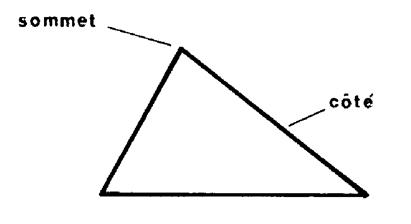
Dans un triangle.
· Il y a 3 sommets · Il a 3 côtés.
Par abus de langage , un triangle désigne aussi bien : · Un ensemble de trois points. · La figure fermée obtenue en joignant deux à deux les trois points limitant des segments (les côtés). · La surface limitée par les segments formant la figure précédente.
Dans la partie qui suit on vous demande de construire des triangles, c'est-à-dire , déterminer les sommets et tracer les côtés à l’aide uniquement d’un crayon, d’une règle et d’un compas ( et d’une équerre pour les triangles rectangles).
2°) Triangles quelconques : construction d’un…
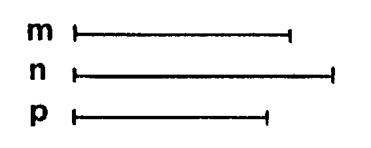
On vous demande de construire un triangle dont les longueurs des côtés sont donnés ci contre. Vous pouvez suivre les différentes étapes proposées ci-dessous pour effectuer cette construction.
Procédure.
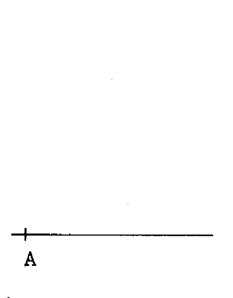
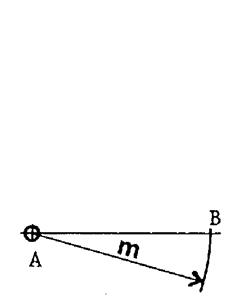
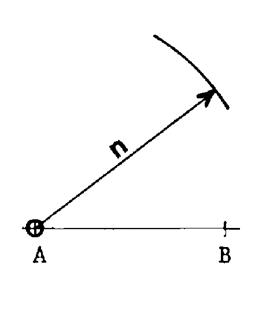
1°) On trace une droite, et, sur cette droite on place un point. Que l’on appelle « A »	2°) Du point « A » , choisi comme centre ,on décrit un arc de cercle de rayon « m » et qui coupe la droite en un point « B ».				3°) De « A » pour centre , on décrit un arc de cercle de rayon « n »
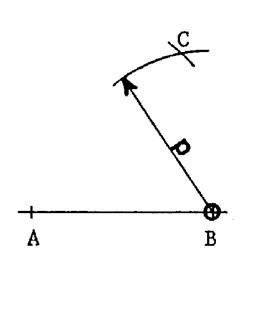
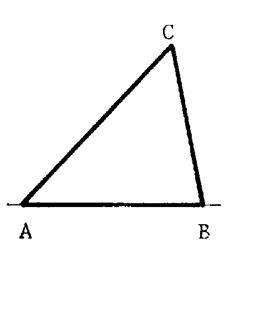
4°) Du point « B » comme centre , on décrit un arc de cercle de rayon « p » . Ces deux arcs se coupent en « C » .	5°)				On obtient alors le triangle C B A
	On trace les segments [ BC ] et [AC ]
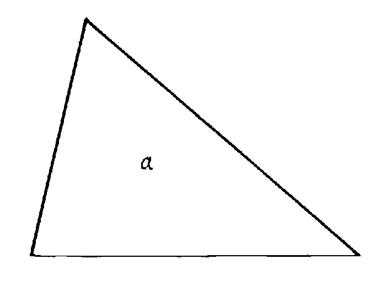
Activité n°1 : en suivant les indications ci-dessus redessiner dans la case d’à côté le triangle « a » et lorsque la construction est terminée nommer « a » ce triangle.
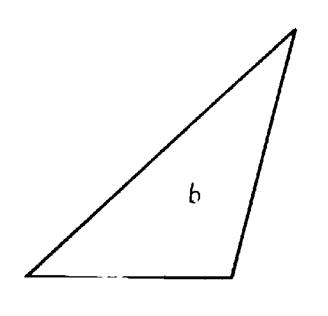
Activité n°2  : en suivant les indications ci-dessus redessiner dans la case d’à côté le triangle « a » et lorsque la construction est terminée nommer « b » ce triangle.
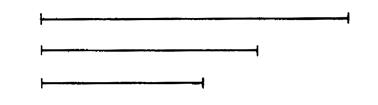
Activité n°3  : en suivant les indications ci-dessus dessiner , en utilisant les segments proposés ci-dessous tracer un triangle « c » dans la case d’à côté et lorsque la construction est terminée nommer « c » ce triangle.
3°) Construction d’un triangle isocèle…
Un triangle isocèle est un triangle dont deux côtés « au moins » ont la même longueur.
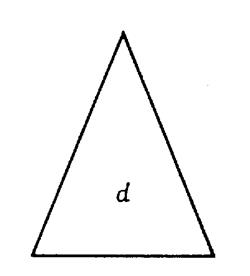
Activité : construire , dans le cadre ci contre ;le triangle isocèle « d »				Triangle « d»
Activité : Construire un triangle « e » , dont les mesures des côtés sont donnés ci dessous
	(pour les deux côtés de même longueur)			Triangle « e »
Activité : Construire un triangle « f » ,dont les mesures des côtés sont donnés ci dessous
	Pour le côté seul.			Triangle « f »
	(pour les deux côtés de même longueur)
4°) Construction d’un triangle équilatéral…
Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur.
Remarque : le triangle équilatéral est , pour trois fois (façons) , nécessairement un triangle isocèle.
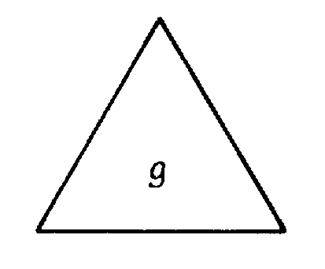
Activité 1 : reproduire (construire) le triangle « g »
			Triangle « g »
Activité 2 :
Construire le triangle équilatéral « h » , on vous donne la longueur d’un côté (ci-dessous)
5°) Construction d’un triangle rectangle …
Pour construire un triangle rectangle , on utilisera ,l’ équerre .
PROCEDURE : Vous suivrez la procédure proposée ci-dessous :
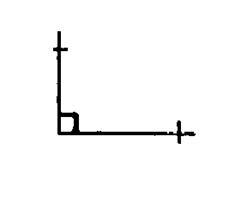
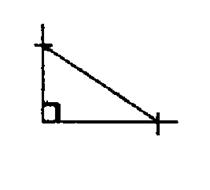
1° ) Avec l’équerre tracer le support de deux côtés : (on a tracé un angle droit)		2°) Reporter la longueur de chacun de ces deux côtés.				3°) Joindre les 2 points obtenus , on a ainsi déterminé le troisième côté.
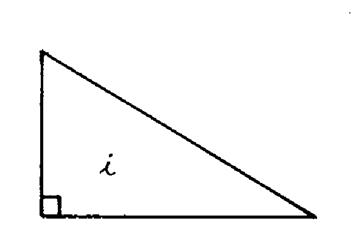
Activité 1 : reproduire ( construire) le triangle rectangle « i », dans le cadre ci contre.
Activité : tracer un triangle rectangle « j » en utilisant les dimensions ci-dessous ;
	« petit côté de l’angle droit »
	« grand côté de l’angle droit »
6°) Construction d’un triangle rectangle isocèle…
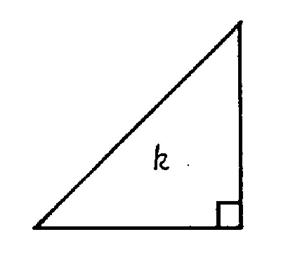
Activité : construire le triangle « k » ci-dessous , qui est un triangle rectangle isocèle.
Acticité : construire les triangle rectangle isocèle « m » ; pour les deux côtés de même longueur on utilisera la longueur du segment ci-dessous.

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Donner la définition  :

· D’un triangle isocèle.

· D’un triangle équilatéral.

· D’un triangle rectangle .

· D’un triangle rectangle isocèle .

EVALUATION:

Refaire les figures ci-dessus