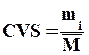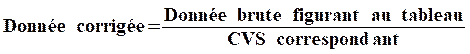|
|
|
||
|
|
|
||
|
|
Les
statistique « bac » |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
EXERCICES
« TYPES » DE STATISTIQUES (niveau bac –bac prof) |
CORRIGE des EXERCICES DE
STATISTIQUES : voir cas
par cas … |
||
|
|
+info cours Séries
statistiques à une variable |
|
|
|
|
|
|
|
Exercice n°1 (ici : corrigé) |
|
|
|
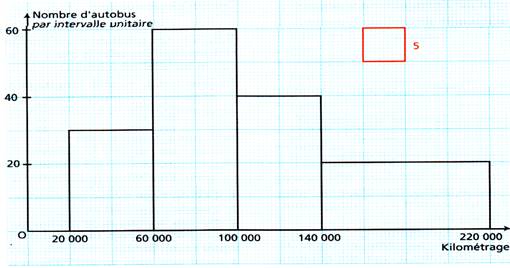
L'histogramme
ci-dessus donne la répartition d'un parc d'autobus en fonction de leur
kilométrage : |
|
|
|
|
|
|
|
a)
Combien
d'autobus ont roulé entre 140 000 km et 220 000 km ? b)
Après
avoir vérifié que le parc contient 170 autobus, calculer le kilométrage
moyen. |
|
|
|
|
|
||||
|
|
Exercice n°2 (ici :corrigé) Une
entreprise a relevé les distances parcourues par ses voitures de société
durant les six derniers mois.
1°)
Calculer le mode, la moyenne et la médiane de cette distribution statistique. 2°) Tracer
le polygone des effectifs cumulés croissants et déterminer graphiquement la
valeur de la médiane. |
|
|
|
|
|
||||||
|
|
Exercice n°3 (ici corrigé) Une
entreprise produit des tubes métalliques. L'analyse d'un échantillon de 100
pièces produites donne le tableau suivant :
1°)
Calculer la moyenne 2°)
Calculer à 1 % près le pourcentage de pièces dont la longueur appartient à l'intervalle |
|
|
|
|
|
||||||
|
|
Exercice n°4 (ici corrigé) Un
fabricant d'ameublement analyse les ventes de tables réalisées durant l'année
écoulée. Il a
obtenu la distribution statistique ci dessous
indiquant le nombre de tables vendues suivant leur prix :
1°)
Calculer le prix moyen on le note : 2°)
calculer l'écart type s. 3°) Donner
le tableau des fréquences, des fréquences cumulées croissantes et
décroissantes. 4°) Tracer
la courbes des fréquences cumulées
croissantes. Déterminer graphiquement la valeur de la médiane. Calculer la
valeur de la médiane. 6°) En
prenant s = 138 €, détermine le
pourcentage de tables dont les prix sont l'intervalle |
|
|
|
|
|
||||||||||||||||||
|
|
Séries statistiques à deux variables Exercice n°5 (ici corrigé) On donne
la série statistique double suivante :
1°)
Déterminer les coordonnées du point moyen G1 des quatre premiers
points du nuage 2°)
Déterminer les coordonnées du point moyen G2 des quatre derniers
points du nuage. 3°) Déterminer
l'équation de la droite passant par les points G1 et G2. 4°)
Représenter le nuage de points et tracer la droite (G1G2). |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
Exercice n°6 (ici corrigé) Le tableau
suivant donne l'évolution du nombre de nuitées réservées dans les gîtes
ruraux d'un département touristique, au cours de dix années
1°)
Représenter par un nuage de points ( xi ;
yi) la série statistique dans un repère orthogonal. On prendra : 1
cm pour 1 année en abscisse 1
cm pour 2 milliers de nuitées en ordonnée ( commencer
à 25 ) 2°) On partage l'ensemble des points du nuage en deux sous ensembles correspondant l'un à aux années 1991 à
1995 et l'autre 1996 à 2000. Déterminer les coordonnées des points moyens G1 et G2
de chacun des sous ensembles précédents. 3°) Déterminer l'équation de la droite passant par les points G1
et G2. 4°) En utilisant l'équation précédente, quel nombre de nuitées
peut-on prévoir en 2003 ? Vérifier sur le graphique. 5°) A partir de quelle année peut-on prévoir le doublement du
nombre de nuitées par rapport à l'année 1991 ? |
|
|
|
|
|
||||
|
|
Exercice
n°7 ( ici
corrigé) La société SLAMA a mis au point un logiciel de gestion destiné
aux PME. Xi désigne le prix proposé ( en
€) et yi le nombre d'entreprises disposées à l'acheter au prix xi L'enquête menée auprès de 500 entreprises a donné les résultats
suivants :
1°) Représenter le nuage de points Mi(xi
; yi) dans un repère orthogonal, d'unités graphiques : Abscisses : 1 cm pour 500 € Ordonnée : 1 cm pour 50
entreprises. 2°) a) Calculer les coordonnées du point
moyen G1 des cinq premiers points du nuage. Calculer les coordonnées du point
moyen G2 des cinq derniers points du nuage. 3°) Placer
les points G1 et G2 dans le repère. Tracer la droite (G1G2).
Déterminer par le calcul, l'équation de la droite (G1G2). 4°) En
utilisant l'équation de la droite (G1G2), Calculer le
nombre d'entreprises disposées à acheter le logiciel si son prix est de 1500
€. 5°) calculer
le prix à proposer si on veut vendre le logiciel à 300 entreprises. 6°) Les
frais de conception et de distribution du logiciel sont de 150 000 €.
Vérifier que le bénéfice de la société SLAMA s'exprime par : B(x) = x ´ (-0,147 x + 612) - 150 000 7°) On
considère la fonction B, définie sur [0 ; 4 000] par :
Montrer
que cette fonction admet un maximum pour une valeur x0 de
l'intervalle [ 0 ; 4 000 ] que l'on calculera. Indication
: calculer
la dérivée de cette fonction. Calculer
alors le bénéfice maximal. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
Séries chronologiques -CVS +Exercice n°8 (ici corrigé) Le rayon
habillement d'un magasin est sujet à des variations saisonnières importantes.
Afin de mieux ajuster les prévisions de commande, on veut prévoir les
chiffres d'affaires des mois d'août et de décembre 1996. On dispose
pour cela des chiffres d'affaires mensuels ( en k€)
de ce rayon pour les deux années précédentes.
1°) Calculer
la moyenne des chiffres d'affaires des deux années 1994 et 1995 pour chaque
mois. Regrouper les résultats dans un tableau. On note mi ( i = 1,2…..,12) ces chiffres d'affaires mensuels moyen. 2°)
Calculer le chiffre d'affaire moyen des 24 mois des deux années. On note ce
chiffre d'affaire moyen 3°)
Déterminer le CVS du chiffre d'affaires pour chaque mois. On rappelle que le
CVS du mois i est :
Arrondir
les résultats à 0,01 près. 4°)
Déduisez les données corrigées des variations saisonnières des chiffres
d'affaires mensuels pour l'année 1995. On donne :
5°)
L'équation suivante donne l'évolution du chiffre d'affaire mensuel en
fonction du mois ( en données corrigées)
, elle a été obtenue à l'aide des données corrigées de l'années 1995 : y = 0,255 x + 153,97 où y
chiffre d'affaire en kk€ et x rang du mois. Calculer
les chiffres d'affaires prévisionnels des mois d'août 1996 (rang 20) et de
décembre 1996 (rang 24). 6°)
Calculez alors les chiffres d'affaires des mois d'août 1996 et de décembre
1996 en données brutes. +Exercice n°9 (ici
corrigé) Une entreprise
de restauration demande une étude statistique de ses ventes réalisées au
cours du dernier exercice. On vous communique dans un tableau l'évolution du
nombre de couverts servis chaque jour.
1°) Représenter
graphiquement cette série chronologique. 2°)
Constituez deux groupes de points : Le premier
: de Janvier à Mai inclus Le second
: de Juin à Décembre a)
Déterminer
les coordonnées des ponts moyens M et S correspondant à chacun des groupes. b)
Déterminer
l'équation de la droite (MS) c)
Représenter
graphiquement cette droite et déterminer graphiquement le nombre moyen de
couverts espéré au cours du mois de mars de l'année suivante. |
|
|
|
|
|
|||||||||
|
|
+Exercice n°10 (ici corrigé) Une
entreprise cherche à établir des prévisions de ventes. Elle dispose pour cela
des chiffres des ventes trimestrielles réalisées en k€ :
1°)
Représenter graphiquement l'évolution des ventes trimestrielles dans repère
orthogonal d'unités graphiques : En abscisses : 1 cm pour 1
trimestre En ordonnée : 1 cm pour 500 k€ ( commencer à 6000 k€) 2°) Calculer
les coordonnées des points moyens G1 et G2 des deux
nuages composés des quatre premiers points pour l'un et des quatre suivants
pour l'autre. 3°)
Calculer l'équation de la droite (G1G2) 4°) Calculer
la moyenne générale trimestrielles des ventes sur les deux années puis la
moyenne des ventes de chacun des quatre trimestre. 5°) En
déduire à 0,001 près la valeur des quatre CVS. 6°)
L'entreprise veut prévoir l'évolution des ventes pour 2001: a)
Déterminer
les ventes trimestrielles de 2001 prévisibles en données corrigés des
variations saisonnières, arrondies à la dizaine d'euros, en utilisant
l'équation de la droite (G1G2). b)
A
l'aide des CVS en déduire les ventes trimestrielles prévisibles pour 2001 en
données brutes. |
|
|
|
|
|
||||||||||||||
|
|
+Exercice n°11 (ici corrigé) Le marché
de l'appareil photo est en pleine expansion. Le relevé des ventes a donné les
renseignements suivants :
1°)
L'objectif initial était une augmentation d'une année sur l'autre de 80 % a)
calculer
les pourcentages d'augmentation des ventes réelles d'une année sur l'autre. b)
L'objectif
a t-il été atteint chaque année ? Préciser. 2°)
Représenter graphiquement les ventes d'appareils jetables de 1989 ( année de rang 1) à 1994 ( année de rang 6) 3°) On
propose deux méthodes pour définir la tendance ( x
est le rang de l'année) : · Utiliser la relation y = f(x) =
1 005x - 1 500 · Utiliser la relation : y = g(x)
=193 x² - 350 x + 330 a)
Pour
x valant 1,2,3,4,5,6 , calculer f(x) et g(x),
présenter les résultats dans un tableau. b)
Tracer
les courbes représentatives des deux fonctions sur le graphique précédent. c)
Préciser
laquelle des deux fonctions de rapproche le plus des ventes réelles. 4°) En
utilisant la tendance la plus proche des ventes réelles : a)
Déterminer
les ventes prévisionnelles en 1995 b)
Déterminer
l'année au cours de laquelle les ventes dépassent de 10 millions d'appareils
jetables. |
|
|
|
|
|
||||||||
|
|
+Exercice n°12 (ici corrigé) Un gérant
de vidéo- club fait le bilan des locations de cassettes vidéos
les trois premières semaines de l'ouverture de son magasin :
1°)
Calculer la moyenne journalière des locations sur les trois semaines à 0,1
près. 2°)
Calculer la moyenne des locations du Lundi, Mercredi et samedi. 3°) En
déduire le CVS du lundi, mercredi, samedi à 0,001 près. |
|
||||||||
|
|
|
|
||||||||
|
|
|
|
||||||||
|
|
|
|
||||||||
|
|
|
|
+