NIVEAU IV : CORRECTION DES EXERCICES DE STATISTIQUES

Exercice n°5

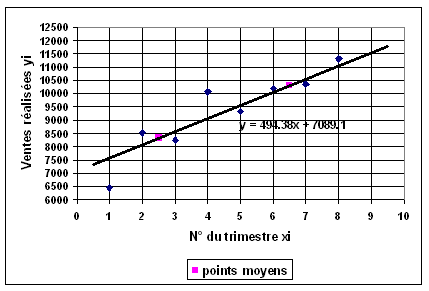
1°) G₁ (2 ; 6,05)

2°) G₂ (5,45 ; 24,25)

3°) Il faut déterminer l'équation de la droite (G₁G₂) de la forme y = ax + b

Calcul du coefficient directeur a C'est le rapport de la différence des ordonnées et de la différence des abscisses des points. .

On est obligé de garder l'écriture fractionnaire pour faire le calcul exact de l'équation de la droite (G₁G₂ )

Calcul de l'ordonnée à l'origine b

L'équation est de la forme . Pour déterminer b on écrit de G₁ appartient à cette droite c'est à dire que ses coordonnées vérifie l'équation : soit :

donc

L'équation de la droite (G₁G₂ ) est soit avec des valeurs approchées : y = 5,2754 x + 4,5007

Vous pouvez vérifier que les coordonnées de l'autre point G₂ vérifie cette équation.

4°)

Exercice n°6

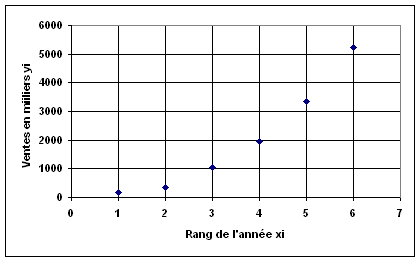
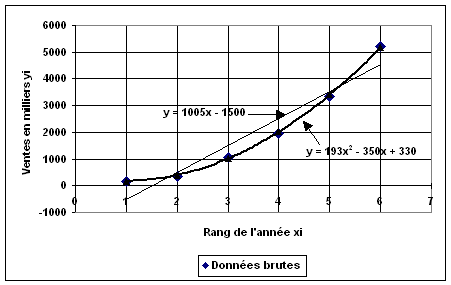
1°)

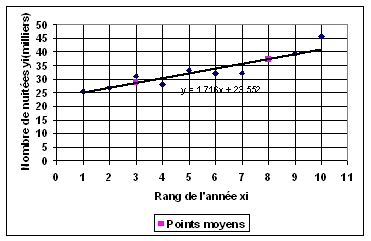
2°) les coordonnées des points moyens sont :

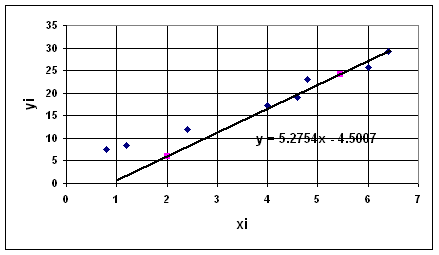
G₁ ( 3 ; 28,7)

G₂ ( 8 ; 37,28)

3°) La démarche est la même qu'à l'exercice n°5.

L'équation de la droite (G₁G₂) :

y =1,716 x + 23,552

4°) Le rang de cette année est x = 13 donc le nombre de nuitées sera :

y = 1,716 ´ 13 + 23,552 = 45,86

5°) Le nombre de nuitées en 1991 est 25,4 le double est donc 50,8. Dans ce cas il faut déterminer quelle est la valeur de x correspondant à y = 50,8.

On doit résoudre l'équation :

50,8 = 1,716 x + 23,552 donc x ≈ 15,88 soit 16 années environ.

Exercice n°7

Voici les réponses

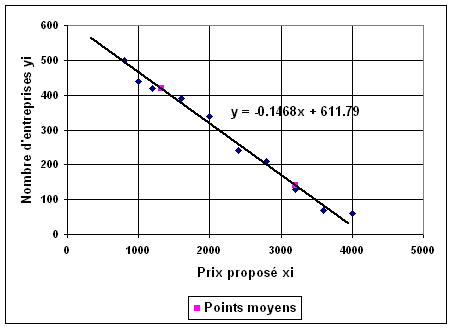1°)

2°) a) Les coordonnées des points moyens sont :

G₁(1320 ; 418)

G₂(3200 ; 142 )

3°) L'équation de la droite (G₁G₂) est :

y = -0,1468 x + 611,79

4°) il faut donc calculer y pour x = 1500 :

y = -0,1468´1500+611,79

y = 391,59.

Il y aurait donc 392 entreprises disposées à acheter le logiciel à 1500 €

5°) Il faut calculer x pour y = 300 : on doit donc résoudre l'équation : 300 = -0,1468´x + 611,79

donc . Le prix à proposer serait donc de 2130 € environ.

6°) Le bénéfice net de la société s'exprime par :

· Les bénéfices liés à la vente du logiciel :

x : prix proposé, y : nombre de logiciel vendus

ce bénéfice est donc : y´x.

Mais d'après la question 5°) y = -0,1468 x + 611,79

Ce bénéfice s'exprime donc par la relation :

(-0,1468 x + 611,79) ´ x

· Les frais de conception et de distribution de 150 000 €

Le bénéfice net B(x) est donc : B(x) = (-0,1468 x + 611,79) ´ x - 150 000 = -0,1468 x² + 611,79 x - 150000

Soit en arrondissant : B(x) = -0,147 x² + 612x - 150000.

7°) Rappel : lorsque qu'une fonction présente un maximum ou un minimum, sa dérivée s'annule (voir le cours sur la dérivée)

Le calcul de la dérivée B' de la fonction B est :

B'(x) = -0,147´2 x + 612 = -0,294 x + 612

La fonction B présente un maximum si B'(x) = 0 soit -0,294 x + 612 = 0.

La solution de cette équation est x = -612/-0,294 ≈ 2081,632653.

La fonction B admet donc un maximum pour x₀ = 2081,632653.

La valeur de ce bénéfice est :

B(2081,632653) = -0,147 ´(2081,632653)²+612´2081,632653-150000 =486979,5918

Exercice n°7

(Dans l'énoncé, les chiffres d'affaires sont en k€)

1°)

	1994	1995	Moyennes mi
Janvier	171.96 k€	160.07 k€	166.02 k€
Février	168.30 k€	173.79 k€	171.05 k€
Mars	147.27 k€	152.75k€	150.01 k€
Avril	139.03 k€	140.86 k€	139.95 k€
Mai	150.92 k€	159.16 k€	155.04 k€
Juin	150.92 k€	171.96 k€	161.44 k€
Juillet	143.61 k€	132.63 k€	138.12 k€
Août	110.68 k€	121.65 k€	116.17 k€
Septembre	173.79 k€	181.11 k€	177.45 k€
Octobre	170.13 k€	178.37 k€	174.25 k€
Novembre	134.46 k€	160.99 k€	147.73 k€
Décembre	181.11 k€	186.60 k€	183.86 k€

	CVS
Janvier	1,06
Février	1,09
Mars	0,96
Avril	0,89
Mai	0,99
Juin	1,03
Juillet	0,88
Août	0,74
Septembre	1,13
Octobre	1,11
Novembre	0,94
Décembre	1,17

2°) Cela revient à faire la moyenne des moyennes m_i :

3°) Voir Tableau

4°) Le tableau des données corrigées des variations saisonnières pour l'année 1995 est :

1995	Données corrigées
Janvier	151,00 k€
Février	159,44 k€
Mars	159,11k€
Avril	158,27 k€
Mai	160,77 k€
Juin	156,74 k€
Juillet	150,72 k€
Août	164,39 k€
Septembre	160,27 k€
Octobre	160,69 k€
Novembre	171,27 k€
Décembre	159,49 k€

5°) Août 1996 x = 20 : y = 0,255´20 + 153,97 = 159,07 k€

Décembre 1996 x = 24 : y = 0,255´24 + 153,97 = 160,09 k€

6°) D'après l'expression du n°4 on a Donnée brute = CVS ´ Donnée corrigée

Donc : Août 1996 : Donnée brute = 0,74 ´ 159,07 = 117,71 k€

Décembre 1996 : Donnée brute: 1,17 ´160,09 = 187,31 k€

Exercice n°8

1°) On va numéroter les 12 mois de 1 à 12. En abscisses on placera le n° du mois et en ordonnée le nombre de couverts correspondant :

2°) a) Le point M a pour coordonnées : M ( 3 ; 90 ) Le point S a pour coordonnées : S ( 9 ; 106 )

b) L'équation de la droite (MS) est : y = 2,667 x + 82

a) Le mois de Mars de l'année suivante a pour rang x = 15. Il faut donc à l'aide de l'équation

de la droite y = 2,667 x + 82.

X = 15 ; y = 2,667´15 + 82 = 122,005 On peut donc espérer 122 couverts en Mars de l'année suivante.

Exercice n°9

1°) il y a 8 trimestres au total on va donc numéroter ces trimestres de 1 à 8.

2°) Les coordonnées des points G₁ et G₂ sont respectivement : (2,5 ; 8325) et ( 6,5 ; 10302,5)

3°) L'équation de cette droite est :

y = 494,38x + 7089,1

4°) La moyenne M trimestrielles des ventes pour les deux années est : 10 345.

La moyenne des ventes de chacun des 4 trimestres m_i est :

Trimestre 1 : 7 890

Trimestre 2 : 9 365

Trimestre 3 : 9 305

Trimestre 4 : 10 695

5°) Rappel CVS = m_i/M. Donc

Trimestres	CVS
1	0,763
2	0,905
3	0,899
4	1,034

6°) a) Les 4 trimestres de 2001ont pour n° 9,10,11,12 donc :

1^er Trimestre : x = 9 donc y = 494,38´9 + 7089,1 = 11538,52 arrondi à la dizaine d'euros : 11540 €

2^eme Trimestre : x = 10 donc y = 494,38´10 + 7089,1 = 12032,9 ≈ 12030 €

3^eme Trimestre : x = 11 donc : y = 12527,28 ≈ 12530 €

4^eme Trimestre : x = 12 donc y = 13021,66 ≈ 13020 €

b) Donnée brute = CVS´Donnée corrigée donc : 1^er Trimestre : 0,763´11540 = 8805,2 €

2^eme Trimestre : 0,905´12030 = 10887,15 €

3^eme Trimestre : 0,899´12530 = 11264,47 €

4^eme Trimestre : 1,034´13020 = 13462,68 €

Exercice n°10

1°) a) pour calculer les pourcentages d'augmentation, on peut utiliser la formule suivante qui est issue de la résolution d'une équation du premier degré à une inconnue (l'inconnue étant le pourcentage x en %)

1989 - 1990 : x = 100 % 1990-1991 : x = 200 % 1991 - 1992 : x = 85,71 %

1992 - 1993 : x = 71,79 % 1993 - 1994 : x = 56,12 %

b) L'objectif n'est pas atteint pour les années 1993 et 1994

2°)

3°) a)

Rang x	1	2	3	4	5	6
f(x)	-495	510	1515	2520	3525	4530
g(x)	173	402	1017	2018	3405	5178

b) Pour tracer les représentations graphiques des deux fonctions f et g, il suffit pour la première d'avoir deux points car c'est une fonction affine et la courbe représentative est une droite d'équation y = 1 005 x - 1 500. On peut prendre par exemple (2;540) et (4 ; 2520)

Pour la seconde, c'est une parabole il suffit de placer tous les points de coordonnées ( x ; g(x) ) calculées dans le tableau précédents et de lisser la courbe obtenus au traçage.

c) La fonctions se rapprochant le plus des ventes réelles est g

4°) il faut donc calculer y pour x = 7

Ainsi :

y=193´7²-350´7+330

y=7337

En 1995 on peut prévoir une vente de 7337 milliers d'appareils.

b) Dans ce cas il faut déterminer le ou les valeurs de x pour lesquelles y = 10 000. On doit résoudre l'équation du second degré : (voir le cours sur les équations du second degré pour les formules)

193 x²-350 x + 330 = 10 000 soit 193 x²-350 x -9670 = 0

Calculons le discriminant : ∆ = (-350)²-4´193´(-9670) = 7587740, il y a deux solutions : x₁ = 8,04297 et x₂ = -6,229

La deuxième solution est à rejeter. L'année ayant le rang 8 verra la vente d'appareils jetables égale à 10 000 miliers.

L'année au cours de laquelle cette condition sera réalisée est donc 1996.

Exercice n°11

1°) La moyenne journalière des locations sur les trois semaines est :

	Moyenne sur les trois semaines	CVS
Lundi Mercredi Samedi	6,3 27,0 34,3	0,352 1,508 1,916

2°)