NIVEAU IV : CORRECTION DES EXERCICES DE STATISTIQUES

Exercice n°7

Voici les réponses

1°)

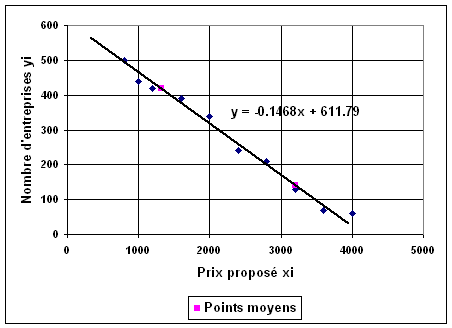
2°) a) Les coordonnées des points moyens sont :

G₁(1320 ; 418)

G₂(3200 ; 142 )

3°) L'équation de la droite (G₁G₂) est :

y = -0,1468 x + 611,79

4°) il faut donc calculer y pour x = 1500 :

y = -0,1468´1500+611,79

y = 391,59.

Il y aurait donc 392 entreprises disposées à acheter le logiciel à 1500 €

5°) Il faut calculer x pour y = 300 : on doit donc résoudre l'équation : 300 = -0,1468´x + 611,79

donc . Le prix à proposer serait donc de 2130 € environ.

6°) Le bénéfice net de la société s'exprime par :

· Les bénéfices liés à la vente du logiciel :

x : prix proposé, y : nombre de logiciel vendus

ce bénéfice est donc : y´x.

Mais d'après la question 5°) y = -0,1468 x + 611,79

Ce bénéfice s'exprime donc par la relation :

(-0,1468 x + 611,79) ´ x

· Les frais de conception et de distribution de 150 000 €

Le bénéfice net B(x) est donc : B(x) = (-0,1468 x + 611,79) ´ x - 150 000 = -0,1468 x² + 611,79 x - 150000

Soit en arrondissant : B(x) = -0,147 x² + 612x - 150000.

7°) Rappel : lorsque qu'une fonction présente un maximum ou un minimum, sa dérivée s'annule (voir le cours sur la dérivée)

Le calcul de la dérivée B' de la fonction B est :

B'(x) = -0,147´2 x + 612 = -0,294 x + 612

La fonction B présente un maximum si B'(x) = 0 soit -0,294 x + 612 = 0.

La solution de cette équation est x = -612/-0,294 ≈ 2081,632653.

La fonction B admet donc un maximum pour x₀ = 2081,632653.

La valeur de ce bénéfice maximal est :

B(2081,632653) = -0,147 ´(2081,632653)²+612´2081,632653-150000 = 486979,5918 €