NIVEAU IV : CORRECTION DES EXERCICES DE STATISTIQUES
Exercice n°11 ( voir le sujet)
1°)
a) pour calculer les pourcentages d'augmentation, on peut utiliser la formule
suivante qui est issue de la résolution d'une équation du premier degré à une
inconnue (l'inconnue étant le pourcentage x en %)
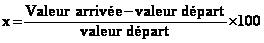
1989
- 1990 : x = 100 % 1990-1991
: x = 200 % 1991 - 1992
: x = 85,71 %
1992
- 1993 : x = 71,79 % 1993 -
1994 : x = 56,12 %
b)
L'objectif n'est pas atteint pour les années 1993 et 1994
 2°)
2°)
3°)
a)
|
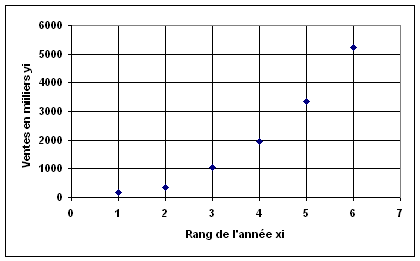
Rang
x
|
1
|
2
|
3
|
4
|
5
|
6
|
|
f(x)
|
-495
|
510
|
1515
|
2520
|
3525
|
4530
|
|
g(x)
|
173
|
402
|
1017
|
2018
|
3405
|
5178
|
b) Pour tracer les
représentations graphiques des deux fonctions f et g, il suffit pour la
première d'avoir deux points car c'est une fonction affine et la courbe
représentative est une droite d'équation y = 1 005 x - 1 500.
On peut prendre par exemple
( 2 ; 540 ) et ( 4 ; 2520 )
Pour
la seconde, c'est une parabole il suffit de placer tous les points de
coordonnées ( x ; g(x) ) calculées dans le tableau précédents et de lisser la
courbe obtenus au traçage.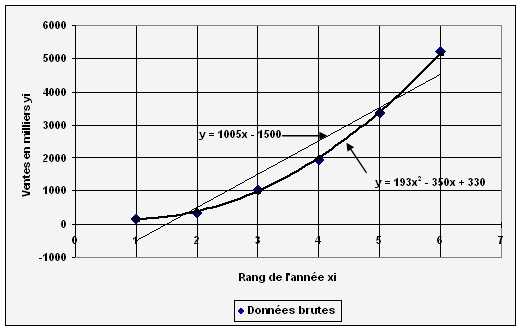
c)
La fonction se rapprochant le plus des ventes réelles est g
4°) il faut donc calculer « y » pour « x = 7 »
Ainsi :
Y = 193´7²-350´7+330
y= 7337
En 1995 on peut prévoir une vente de 7337 milliers
d'appareils.
b) Dans ce cas il faut déterminer le ou les valeurs
de x pour lesquelles y = 10 000. On doit résoudre l'équation du second degré :
(voir le cours sur les équations du second degré pour les formules)
193 x² - 350 x + 330 = 10
000 soit 193 x² - 350 x - 9670 = 0
Calculons le discriminant : ∆ = (-350)²-4´193´(-9670) = 7587740, il y a
deux solutions : x1 = 8,04297 et x2 = - 6,229
La deuxième solution est à rejeter. L'année ayant
le rang 8 verra la vente d'appareils jetables égale à 10 000 miliers.
L'année au cours de laquelle cette condition sera
réalisée est donc 1996.
![]()

