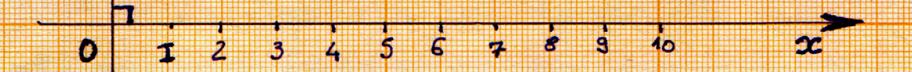Pré requis

La règle graduée ( graduation)
Les nombres positifs et négatifs
Les outils de mesure de longueurs
Les ensembles de nombres
Relations d’ordre dans les nombres entiers naturels
Nomenclature (terminologie)

ENVIRONNEMENT du dossier

INDEX   warmaths.	Objectif précédent :   Lieux géométriques  et détermination d’un point	Objectif suivant :abscisse positive d’un point	1°) Tableau       2°) Liste des cours sur le repérage
		Les Repères : repérage d’un point dans un repère cartésien      3°) Repérage des nombres

DOSSIER :    L’   AXE  dans le repèrage…

	-         Repère sur une droite et droite graduée (définition).
	-          Tracer d’un axe
	-         Axe horizontal
	-         Axe vertical
	-         Axes sécants et repère cartésien.
	-         Repèrage dans l’espace : avec trois axes sécants.
	-         Le papier millimétré….
	-
	-         INFO sur le  :« SENS positif ou négatif »
TEST	COURS	Devoir  Contrôle	Devoir évaluation	Interdisciplinarité		Corrigé Contrôle	Corrigé évaluation

 

Info plus +++++: voir mesure algébrique d’un bipoint « d’origine O et d’extrémité A »

 

COURS

 

 

 

On appelle « axe » une droite sur laquelle on a choisi un sens de parcours qu’on appelle le sens positif .

Ce sens est indiqué à l’aide d’une flèche . On dit que la droite est « orientée » ; Cette flèche est  ,par convention, confondue avec la droite graduée .

Le sens opposé au sens  positif est le sens « négatif ».

 

 

Repère d’une droite :

Une unité de longueur étant choisie ( le cm  ou un carreau par exemple) ,nous plaçons sur la droite un point O le point I  que l’on appelle « bipoint (O,I ) » tel que la distance  de O à I égale « 1 ».

Notation :  d(O,I) = 1   ( dans cette unité )

Le bipoint (O,I) est appelé « repère de la droite »

Ce repère détermine :

-         une unité de longueur .

-         un sens ( par convention le sens positif est de O vers I )

 

         La droite  munie du bipoint ( O,I) est appelée «  axe » .

 

Ainsi , tout point de la droite est repéré par un nombre appelé « abscisse ».

Et inversement , tout nombre est l’abscisse d’un point sur une droite  et d’un seul.

 

 

En résumé : On appelle « axe » une droite graduée régulièrement  orientée ,il possède un segment unitaire de valeur « 1 » , et une origine « O »

 

 

Remarque : la règle graduée n’est pas orientée , sur la droite graduée il n’est pas tracé de flèche indiquant un sens .

                      

Tracé d’un axe	Exemples
Axe horizontal :   On trace une droite au bout de laquelle on place une flèche indiquant un sens. Ensuite , on gradue à partir d’un segment unitaire. Chaque graduation est repéré par un nombre positif  et ou négatif .                     Le segment  unitaire , est noté  [ O,I ] ,  il est de valeur  1   (une unité)  ,et il est  attribué à la droite horizontale ,dite  « droite d’abscisse  « x » ».
Axe vertical :       Le segment  unitaire ,   noté  [O, J] , de valeur  1   (une unité)  ,est attribué à la droite  coupant la droite horizontale , dite  « droite d’ordonnée  « y » ».

 

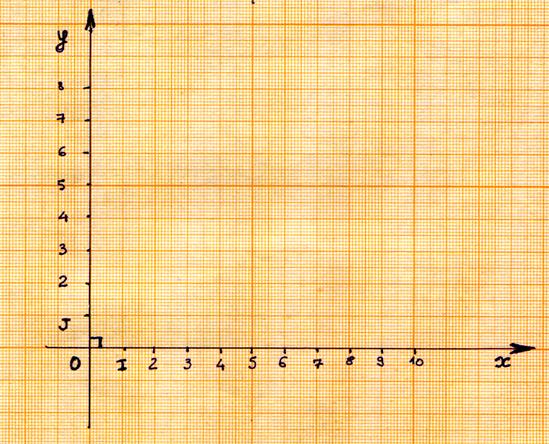
Info 1 :  Deux axes  sécants forment un repère dit « cartésien »
Ces deux segments unitaires forment  une base un objet à sa position définie à partir de deux informations.   ·      La droite O x est appelée : axe des  abscisses , ·      La droite Oy est appelée : axe des  ordonnées.  ,
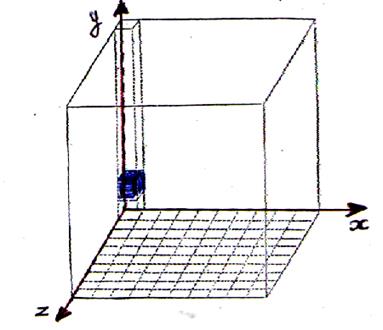
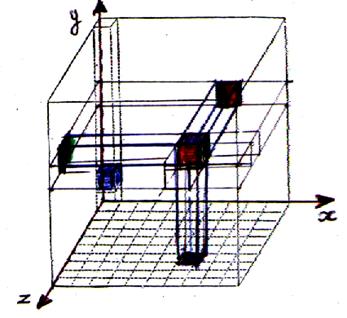
Info 2 : Trois axes sécants forment un repère dans l’espace (la position du cube est défini à partir de  trois dimensions  )

 

 

 

Exemple d’axe gradué  sur papier millimétré

 

 

 

INFO 3 :« SENS positif ou négatif » 

 

SENS DE LECTURE des nombres :

               ce   sens  est le même que celui utilisé pour lire les mots  (de gauche à droite, )

remarque : Notre sens de lecture n’est pas internationale ; le sens de lecture en langue arabe est de droite à gauche , pour la langue chinoise , japonaise le sens est de haut vers le bas.  

 

                     A  )  soit une droite orientée  (une flèche indique le sens de déplacement)

 

 

 

 

Par convention:

-    si l’on va de la gauche vers la droite ,on se déplace dans le sens « positif »

 

 

-    si l’on va de la droite vers la gauche ,on se déplace dans le sens « négatif »

 

 

 

 remarque : la position du « Zéro » ne détermine pas un sens

                           à droite du zéro   ;les nombres sont « positifs »  et  classés par ordre croissant .( la plus petite valeur absolue à gauche de la plus grande valeur absolue)

                ( exemple : 2 avant 3   ce qui se note   +2 < +3  )

                        à gauche du zéro : les nombres sont dits « négatifs » ; plus la valeur absolue est grande , plus le nombre est petit , ainsi –3 est plus petit que –2 ; donc  « -3 » se trouvera à gauche du nombre « -2 »

                  (exemple  -3 est avant –2  ,cela signifie qu’  à partir de la droite sur la droite graduée on dit  « moins trois est plus petit que moins deux »   ce qui se note –3 < -2   )

 

Voir : la représentation graphique des nombres

CONTROLE:

 

Donner la définition d’un axe

 

 

 

 

 

EVALUATION

 

                                    Construire un axe gradué