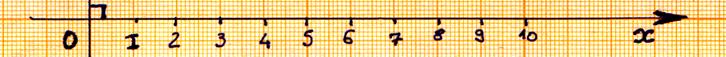Pré requis
|
Construction d’une droite ou axe
gradué ; (La règle graduée) |
|
|
|
|
ENVIRONNEMENT du dossier
|
Tableau Classe 6éme
|
DOSSIER <Repérage> :ABSCISSE
« positive » D’UN POINT .
|
TEST |
COURS |
Interdisciplinarité |
|
REPERAGE
d’un point sur un AXE ou « droite graduée orientée » avec
les nombres positifs
Rappel :
|
Axe gradué avec des nombres entiers positifs |
|
|
Le
segment unitaire , noté [
O,I ] , de valeur 1
(une unité) ,est attribué à la
droite horizontale ,dite « droite d’abscisse « x » ». |
|
AXE : on appelle « axe » une droite
graduée régulièrement orientée ( le sens
est indiqué à l’aide d’une flèche) , il
possède un segment unitaire de valeur « 1 » , et une origine
« O ».
Le sens opposé au sens positif est le sens négatif .
Exemple de graduations d’un axe sur papier millimétré avec des nombres
décimaux positifs
|
|
|
COURS
Si , ayant fixé une unité de longueur , on choisit sur un axe un point O
appelé « origine » , à tout point « A » de l’axe on peut
faire correspondre un nombre algébrique ayant :
1°)
pour valeur absolue le nombre qui mesure le segment OA ,
2°)pour signe le signe + si pour aller de O vers A on se dirige dans le sens positif sur
l’axe ,
et le signe « - » si on se dirige dans le sens négatif .
ce
nombre algébrique s’appelle « l’ abscisse »
du point A .
Réciproquement
, à tout nombre algébrique on peut faire correspondre un point d’un
axe et un seul .
Autrement dit
, tout point d’un axe peut être
déterminé par son abscisse.
Rendre compte de
l’abscisse d’un point :
Chaque point marqué sur une
droite est nommé par une lettre
majuscule et il est associé à une valeur numérique .(positive
ou négative)
Exemples : A(+2) ; B (-1) ; C
(+4)
La valeur absolue
du nombre relatif nous informe sur le
nombre de graduation qui se trouve entre
le point considéré et l’origine des graduations (point O) .
Exemples :
A(+2) : la valeur absolue de +2 est
2 ; le point A se trouve à 2 graduations de l’origine ( point O)
B (-1) la valeur absolue de -1 est 1 ; le
point B se trouve à 1 graduation de
l’origine ( point
O)
C (+4) la valeur absolue de +4 est 4; le point C se trouve à 4 graduations de l’origine ( point O)
* L’abscisse d’un point est un
nombre relatif qui indique la position
de ce point sur une droite graduée.
Exercice : placer sur la droite
graduée les points suivants :
A(+2) ; C (+4)
segment unitaire :1 A C B
![]()
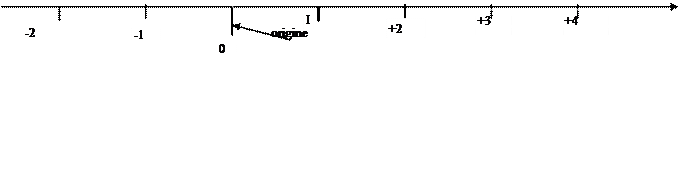
ON dit que le point : .A.... à pour
« abscisse »
: « plus 2 » ;
que l’on note mathématiquement: A (+2 )
ON dit que le point .:..C... à pour
« abscisse »
: « plus
quatre » ; que l’on note mathématiquement:
C (+4)
Exercices
Soit une droite :
a)
terminez la graduation et donnez la valeur de l’abscisse des points :
G ;O ;F ;E ;C
G O F E C
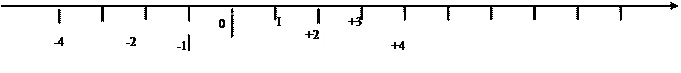
b) Placer les points : M (+5) ; P (-4)
|
les dixièmes
d’unités. Chaque graduation « 1 unité » peut se subdiviser en 10 parties égales.(nous
obtenons les dixièmes d’unités) |
|
|
|
Ces 10 parties égales peuvent se subdiviser aussi en 10 parties égales . .(nous obtenons les
dixièmes d’unités) |
|
|
et ainsi de suite
chaque subdivision peut encore se diviser en 10 parties égales. .(nous obtenons les
millièmes d’unités)
|
|
|
|
TRAVAUX AUTO FORMATIFS.
1.
Que veut dire
« graduer »?
2.
De combien de façons peut-on graduer régulièrement une droite ?
3. Quel outils utilise-t-on pour graduer une droite de façon régulière?
4.
Quelle est la fonction du segment unitaire?
5.
Quelle différence y a t - il entre la
« graduation régulière et la graduation
irrégulière ?
EVALUATION
A ) Graduation au
compas :
|
Activité : avec le compas gradué la droite orientée
, placer le point « A » en + 3 et
« B » en - 1 |
|
|
|
Activité : avec le compas gradué la droite orientée
, placer le point « A » en + 3 et
« B » en - 1 |
|
|
|
Activité : avec le compas gradué la droite orientée
, placer le point « A » en + 3 et
« B » en - 1 |
|
|
B )
GRADUATION avec règle graduée:
Série 1 :Conditions :
l’unité 1 à pour mesure 1 cm.
1°) Graduer une droite avec des entiers
naturels .( N ) inférieur à 10
2°) graduer une droite avec des nombres décimaux positifs
( allant de 0,5 en 0,5 ) inférieur à 10
3°) graduer une droite avec des nombres décimaux positifs
( allant de 0,25 en 0,25 ) inférieur à 10
4°)Graduer une droite avec des nombres entiers
relatifs compris entre –10 et +10
5°) graduer une droite avec des nombres décimaux relatifs
( allant de 0,5 en 0,5 ) inférieur à 10
6°) graduer une droite avec des nombres décimaux relatifs
( allant de 0,25 en 0,25 ) inférieur à 10.
Série 2 : Conditions :
l’unité 1 mesure 2 cm.
1°)
Graduer une droite avec des entiers naturels .(
N ) inférieur à 10 , supérieur à -5
2°) graduer une droite avec des nombres
décimaux positifs ( allant de 0,5 en
0,5 ) inférieur à 10 supérieur à -5
3°)
graduer une droite avec des nombres décimaux
positifs (
allant de 0,25 en 0,25 ) inférieur à 10 supérieur à -5
4°)Graduer une
droite avec des nombres entiers relatifs compris entre –10 et +10 supérieur à
-5
5°) graduer une droite avec des nombres
décimaux relatifs ( allant de 0,5 en
0,5 ) inférieur à 10 supérieur à -5
6°) graduer une droite avec des nombres
décimaux relatifs ( allant de 0,2 en
0,2 inférieur à 10 supérieur à -5.
7 ° )
Exercices : Sur une droite graduée
placer les points suivants :
p ; 1/3 ; -1,2 ; ![]()
![]() ;
;![]() ;
;![]()
.