(programme 4^ème )	4^ème collège
Pré requis:
Le rectangle
Le parallélogramme

ENVIRONNEMENT du dossier:

Index : accueil warmaths

Objectif précédent : 1. Les caractéristiques du parallélogramme. 2. Le losange (cours)

Objectif suivant : L’aire du losange.

1°) les figures géométriques Ici les modules Arithmétiques. Liste des cours de géométrie plane

DOSSIER « quadrilatères » : LE LOSANGE ( vu au collège)

	1 ) Définition et propriétés.
	2) Comment reconnaître qu’un quadrilatère est un losange.
	Cours vus en 6^ème et en 5^ème sur les quadrilatères .……et sur le parallélogramme en 6^ème et 5^ème )
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
				Fiche arithmétique

COURS : LE LOSANGE ( vu eu 4^ème collège)
1 ) Définition et propriétés.
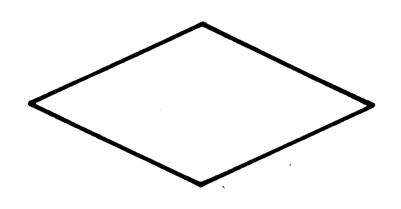
On appelle « losange » tout parallélogramme ayant deux côtés consécutifs de même longueur.
Propriété n °32 Si un quadrilatère est un losange alors ses quatre côtés ont même ..longueur..
Propriété n °33 Si un quadrilatère est un losange alors il admet deux axes de symétrie qui sont ses ..diagonales…
Activité 1 : tracez les sur la figure ci-dessus.
Propriété n °34. Si un quadrilatère est un losange alors ses diagonales sont perpendiculaires.
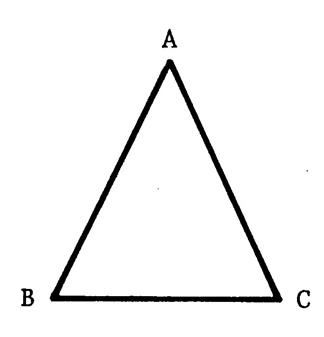
Activité n°2 : Soit ci –contre le triangle isocèle « ABC » de base [ BC ]. Tracez par « B » la parallèle à (AC ) et par « C » la parallèle à ( AB ). Ces deux droites se coupent en « D ». Démontrez que (AD) est perpendiculaire à ( BC ).
2) Comment reconnaître qu’un quadrilatère est un losange.
La première façon de reconnaître un losange : c’est reprendre sa définition. (et comparez )
Ci-dessous nous allons revoir d’autres façons que vous avez étudiez en classes précédentes …..
Propriété n °35. Si un quadrilatère a ses diagonales par axes de symétrie alors ce quadrilatère est un losange.
Propriété n °36. Si un quadrilatère a ses diagonales perpendiculaires alors ce parallélogramme est un losange.
Propriété n °37. Si un quadrilatère a quatre côtés de même longueur alors ce quadrilatère est un losange.
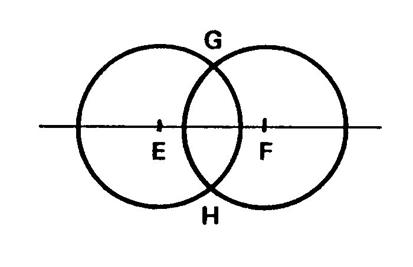
Activité n°3 : Deux cercles de centre « E » et « F » ont même rayon. Ils se coupent en « G » et « H ». Démontrez que « EGHF » est un losange.
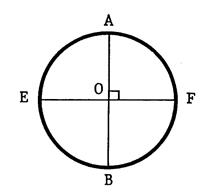
Activité n°4 : « OAB » est un triangle rectangle en « O ». « C » est le symétrique de « A » par rapport à « O ». « D » est le symétrique de « B » par rapport à « O ». Faire la figure puis , Démontrez que « ABCD » est un losange.

Le losange.

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1) Qu’est qu'un losange ?

2 ) Quels sont ses caractères communs au parallélogramme , et quels sont ses propres caractères ? (propriétés )

EVALUATION

1) Construire un losange , sachant que son coté mesure 3 cm et l'un des angles aigus vaut 75°

2) Construire un losange ABCD sachant que la diagonale AC = 4 cm et = 70°

3) Un losange a pour diagonales 60 cm et 80 cm .

Quel est la longueur de son côté ? ( SOS cours+++)

TRACER :

Losange ABCD tel que AB = 27 mm et = 100°

Losange ABCD de diagonales AC = 46 mm et BD = 38 mm

Losange ABCD de diagonale BD = 4 cm et tel que = 70°

En plus : losange d’aire A = 6cm² et de diagonale AC = 3 cm

INTERDISCIPLINARITE