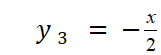|
FL 4 généralités. |
Pré requis
|
|
|
|
|
|
|
Les Grandeurs
proportionnelles |
ENVIRONNEMENT du
dossier :
|
|
|
|
|
DOSSIER : L’
EQUATION de la
FONCTION LINEAIRE.
2°)Obtention d’ une équation à partir
d’un graphe
3°)
Obtention d’
une équation à
partir d’un tableau
4°)
Obtention d’ une
équation à partir d’une représentation
graphique
|
TEST |
COURS |
Interdisciplinarité |
|
ORGANIGRAMME
MODELES MATHEMATIQUES de représentation de la fonction linéaire
cet objectif traite des généralités sur la fonction
linéaire :
Une
fonction linéaire peut s’identifier à partir de quatre modes de
représentation :
A) Equation
B) Graphe
C) Tableau
de variation (de proportionnalité)
D) Représentation
graphique.
Dans ce cours nous prenons
l’équation:
y
= ![]() x est pris comme exemple.
x est pris comme exemple.
(elle est de
la forme « y = a x
» ; dans l’exemple
« a » = ![]() )
)
Les
transformations possibles :
|
|
Equation
|
Graphe
|
Tableau
|
Représentation
graphique
|
Equation
|
|
|
|
|
Graphe
|
|
|
|
|
Tableau
|
|
|
|
|
Représentation
graphique
|
|
|
|
|
1°) l’
EQUATION
On peut obtenir une équation
à partir : d’un graphe ; d’un
tableau de proportionnalité ; d’une représentation graphique.
L’ équation de la fonction linéaire est de la
forme 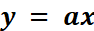
La notation mathématique de la fonction
linéaire :
![]()
Traduction en langage littérale : il y a «
fonction » où « x » a
pour image « a » fois
« x ».
Ce que signifie : « 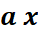 »
»
«![]() »
est appelé
« la variable » de la fonction.
»
est appelé
« la variable » de la fonction.
« ![]() »
est un nombre donné, (bien entendu
différent de zéro ; dans ce cas la fonction linéaire n’existerait pas pour
« 0 » multiplié par « x » égal « 0 » ) ;
»
est un nombre donné, (bien entendu
différent de zéro ; dans ce cas la fonction linéaire n’existerait pas pour
« 0 » multiplié par « x » égal « 0 » ) ;
le nombre «![]() » est
appelé « coefficient directeur »
dans la représentation graphique .
» est
appelé « coefficient directeur »
dans la représentation graphique .
Le nombre « ![]() » est
aussi appelé « coefficient de proportionnalité »
.
» est
aussi appelé « coefficient de proportionnalité »
.
Exemple : on donne
l’équation 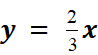 ;
;
« ![]() » est le coefficient de
proportionnalité, il est aussi appelé « coefficient directeur »
» est le coefficient de
proportionnalité, il est aussi appelé « coefficient directeur »
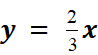 est une équation d’une « fonction linéaire » parce
qu’elle est de la forme
est une équation d’une « fonction linéaire » parce
qu’elle est de la forme ![]()
On notera cette
fonction par l’écriture
symbolique : 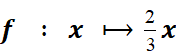
On lira en en langage littérale : « il y a fonction » où « x » a pour image « ![]() » fois
«
» fois
« ![]() ».
».
Signification
de l’écriture : «![]() »
»
«![]() » est appelé « coefficient directeur » dans la
représentation graphique et «
» est appelé « coefficient directeur » dans la
représentation graphique et « ![]() » est
la variable de la fonction.
» est
la variable de la fonction.
On dira que :
La fonction linéaire de
coefficient « ![]() » fait correspondre à chaque valeur de la variable
« x » le nombre «
» fait correspondre à chaque valeur de la variable
« x » le nombre «![]() ».
».
* L’équation représentant de la
fonction linéaire est une équation du
premier degré à deux inconnues de la forme 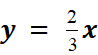
D’autres exemples d’équations représentantes de la fonction
linéaire :
|
|
|
|
Plus généralement :
On dira
que
L’équation représentant de la fonction linéaire est une équation du premier degré à deux
inconnues de la forme y = a x ;
« a » étant le coefficient de l’équation de la fonction linéaire
Le rapport de « ![]() »
sur «
»
sur « ![]() » est , pour la
fonction linéaire, égal au rapport
«
» est , pour la
fonction linéaire, égal au rapport
« ![]()
![]() »
sur «
»
sur «![]() » ;
» ;
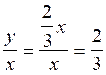
Dans la fonction linéaire ce nombre est constant il est égal à «![]() »
»
Ce nombre «![]() » est appelé « coefficient de
proportionnalité » ;
» est appelé « coefficient de
proportionnalité » ;
Le tableau
s’appellera « tableau de proportionnalité ».
2° ) Obtention
d’ une équation à partir d’un graphe :
CALCUL DE « ![]() »
à partir d’un couple de nombres représentant une fonction linéaire :
»
à partir d’un couple de nombres représentant une fonction linéaire :
En
vue d’obtenir une équation de la forme y = ax
On analyse le graphe : G
= {( 0 ; 0) ; (3 ;2) ; (9 ; 6
) }
On reconnaît
que la droite passe par zéro .on peut
dire le troisième couple de nombres (9 ; 6 )
est de la forme ![]() ;
;
Nous pouvons en déduire que le graphe représentant une fonction linéaire
est d’équation ![]() .
.
;le nombre « 9 » est la valeur
de « ![]() » ;le
nombre « 6 » est la valeur de «
» ;le
nombre « 6 » est la valeur de « ![]() » ;nous
remplaçons ces valeurs dans l’équation (
» ;nous
remplaçons ces valeurs dans l’équation (
![]() devient
devient
![]() , nous en déduisons que a =
, nous en déduisons que a =![]() , après
simplification a =
, après
simplification a =![]()
nous
concluons : le graphe G = {( 0 ;
0) ; (3 ;2) ; (9 ; 6 ) } donne l’équation de la
fonction linéaire y = ![]() x
x
3°) Obtention
d’ une équation
à partir d’un tableau de
proportionnalité :
On nous donne le tableau suivant :
|
|
A |
B |
C |
O |
D |
E |
F |
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
On
nous déclare que le tableau est un tableau de proportionnalité !
On sait qu’en faisant le calcul du rapport ![]() on trouve une valeur à
«
on trouve une valeur à
« ![]() »
»
Ainsi on prend un point ( E ) on identifie
![]()
On fait le calcul : ![]() =
= ![]()
Donc si ![]() ; l’équation de la fonction linéaire
représentant le tableau sera
; l’équation de la fonction linéaire
représentant le tableau sera ![]()
Vérification :
les couples de nombres
forment une suite de rapports ; ils faut vérifier si ils forment
une suite de nombres proportionnels ou
une suite de rapports
égaux
![]() = ? =
= ? = ![]() = ? =
= ? = ![]() = ?=
= ?=![]() = ?=
= ?=![]() = ?=
= ?=![]()
il faut faire les
calculs ! ! !
ou voir la « somme des rapports égaux »
4°) Obtention d’ une
équation à partir @ d’une représentation
graphique.
|
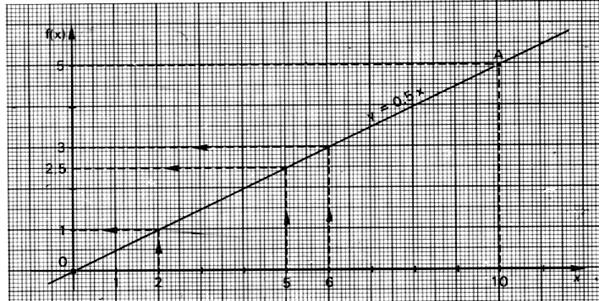
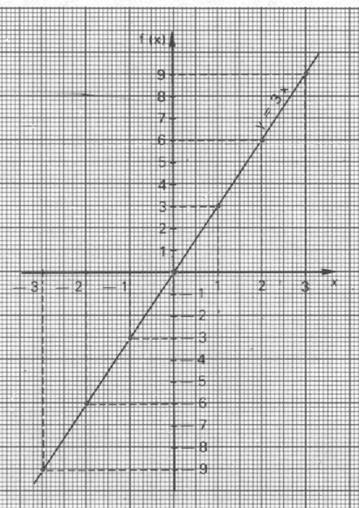
On
choisit un point et l’on relève ses coordonnées : Le point A à pour abscisse et pour ordonnée |
|
Il faut faire le rapport de ![]() pour avoir le coefficient « a » :
pour avoir le coefficient « a » : ![]() = + 0,5
= + 0,5
Nous remplaçons dans
l’équation ![]() ;
«
;
« ![]() »
par la valeur (+ 0,5)
»
par la valeur (+ 0,5)
Cela
donne : ![]()
On
simplifie l’écriture (+ 0,5) = 0,5
Conclusion : la droite à pour équation ![]()
|
|
Travaux auto-formatifs. |
|
|
|
|
|
1°) Donnez le modèle mathématique de l’équation représentant la fonction linéaire.
2°) Que peut-on représenter à
partir d’une équation représentant la
fonction linéaire ?
3°) Soit la notation « ax » , comment nomme - t - on
les facteurs ?
4°) pour trouver le coefficient « a » ,
dans l’équation de la fonction linéaire , quel rapport doit –on faire ?
5°) Donner des exemples
d’équations représentantes de la
fonction linéaire.
( donner les deux couples particuliers)
1°) Soit le graphe ;
représentant une fonction linéaire
G = {( 0 ; 0) ; ( 1 ; 3
) ;( 2 ; 6 ) ; }
Retrouver son équation .
2°) Soit le tableau de
variation représentant d’une fonction linéaire
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
Retrouver son équation .
3° ) Soit la représentation graphique , retrouvez son équation
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tracé :
B A O
![]()
![]()
![]()