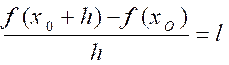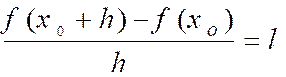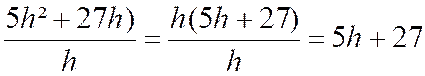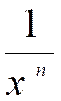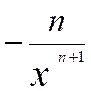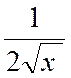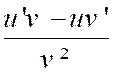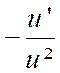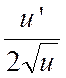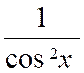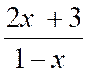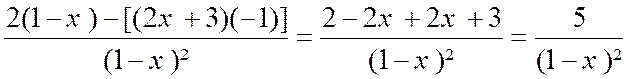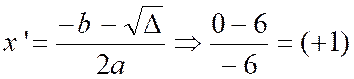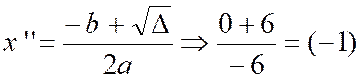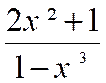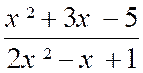Pré requis:
|
Info : liste des connaissances en algèbre
préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
AVANT :
|
APRES :
|
Complément d’Info :
Info complément
cours de niveau IV : sur « la dérivée » Liste des cours : prépa concours
A consulter pour compléments : |
||
|
|
|
|
|
|
TITRE : COURS sur la
Dérivée et L’ ETUDE de FONCTIONS NUMERIQUES - APPLICATIONS
Calcul de la dérivée pour déterminer
les divers sens de variation de la fonction ( tableau
de variation)
·
Dérivée en un point .
·
Interprétation graphique. (exemple) :
·
l’équation de la tangente.
·
Fonction dérivée d’une fonction.
·
Signe de la dérivée et sens de variation de la fonction.
Travaux ;
devoirs
|
|
Corrigé du :
|
|||
|
|
Contrôle |
évaluation |
|||
COURS
Pré
requis : La tangente en un point d’une courbe
A) Dérivée en un point .
· Soit
x0 , un élément d’un intervalle ]a ;b[
. On considère une fonction , f définie sur un ensemble
D contenant ]a ;b[ . Soit . On appelle h un réel
, on appelle « dérivée « de f
pour x = x0 la limite
( si elle existe) du rapport : 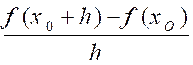 quand h tend vers 0 .
quand h tend vers 0 .
|
|
lim |
|
|
|
|
|
h ® 0 |
|
|
|
Notation : y’0 ou f ’ (x0)
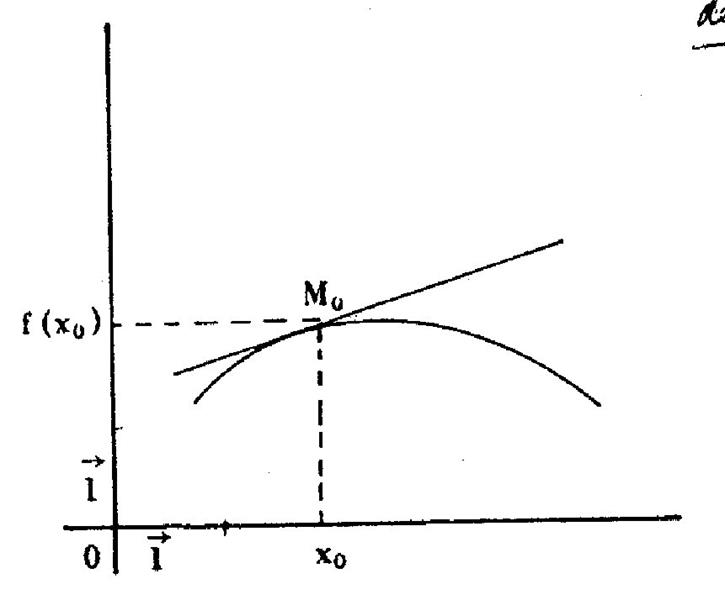
· Interprétation graphique :
|
Pour qu’une fonction y = f(x) admette en x0
une dérivée, il faut et il suffit que la courbe représentative admette au
point d’abscisse x0 une tangent (non parallèle à y0.) Le coefficient directeur de cette
tangente est égal à la dérivée de la
fonction pour x = x0 Equation de la tangente : y = f ’ (x0) . ( x – x0) + f (x0) Remarque :
f ’ (x0) est la dérivée…… |
|
Exemple : Soit la fonction f(x) = 5 x² + 7 x + 4
Questions :
· Trouver
la dérivée au point xO = 2
· Déterminer
l’équation de la tangente.
|
Calcul de la dérivée au point xO
= 2 |
|
|
|
|
Calcul de
f (x O) pour x O = 2 ; ·
f
(2) = 5 (2 )² + 7 (2) + 4 ·
Soit 20 + 14 + 4 = 38 |
Calculatrice : taper : [ 5 (2 )² ] + [ + 7 (2)] + ( + 4) |
|
|
|
|
|
|
Calcul de
f (x O + h ) ; avec
x O = 2 ·
f
(2 + h ) = 5 (2 + h )² + 7 (2 + h ) + 4 |
(2 + h )²
= (2 + h ) (2
+ h ) = 4 + 2 h + 2 h + h² = 4 + 4 h +
h² = 5 ( 4 + 4 h + h²
) =
20 + 20 h + 5 h² |
|
|
·
f
(2 + h ) = 20 + 20 h + 5 h² + 14 + 7 h + 4 = 5 h² +27 h + 38 |
|
|
|
|
|
|
|
Calcul de
f (x O + h ) - f (x O) = ·
= 5 h² +27 h + 38 - 38 ·
= 5 h²
+27 h |
|
|
|
|
|
|
|
Calcul de |
|
|
|
|
|
Ainsi :
|
|
lim |
5 h + 27
|
|
= 27 |
|
|
h ® 0 |
|
|
|
Lire :
la limite de 5 h + 27 quand
« h » tend vers 0 est
égale à « 27 »
|
·
l’équation de la tangente. |
|
|||||||||||
|
|
y
= 27 ( x – 2
) + 38
= 27 x – 54 +38 y
= 27 x – 16 |
|
||||||||||
|
|
Nota : « dérivée et
continuité » Si la fonction « f » admet une dérivée en x O ( la réciproque
n’est pas vraie ) |
|||||||||||
|
|
|
|
||||||||||
|
·
Fonction dérivée d’une fonction. |
||||||||||||
|
|
Soit « f » une fonction admettant
une dérivée « f ’ (xO) » pour
toute valeur xO d’un intervalle ]
a , b [ ; la fonction qui a tout xO
de ] a , b [ associe le nombre dérivée « f’ (xO) »
s’appelle « fonction dérivée ». |
|
||||||||||
|
|
Notation :
« f ’» Par abus de langage, on dit souvent
« dérivée » au lieu de « fonction dérivée » |
|
||||||||||
|
|
||||||||||||
|
|
Valeur
de la fonction « f ( x) » ; y
= |
Valeur de la fonction dérivée « f ‘( x) » ;
y ‘ = |
|
|
||||||||
|
|
|
y
=C (constante) |
y
‘ = 0 |
|
|
|||||||
|
|
|
y
= x |
y ‘ = 1 |
|
|
|||||||
|
|
|
y
= x² |
y
‘ = 2 x |
|
|
|||||||
|
|
|
y
= x3 |
y
‘ = 3 x² |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= x n ; ( n |
y
‘ = n x n-1 |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= |
y
‘ = |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= |
y
‘ = |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
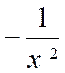
y
= |
y
‘ = |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
Fonction ( y
) |
Dérivée ( y’) |
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= u + v |
y ‘
= u ’ + v ‘ |
|
|
|||||||
|
|
|
y
= u + v + w |
y
‘ = u ’ + v ‘ + w ’ |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y = k u ( k :
constante) |
y
‘ = k u ’ |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= u v
|
y
‘ = u ‘ v + u
v ‘ |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= |
y
‘ = |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= u ² |
y
‘ = 2 u . u’ |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
=u 3 |
y
‘ = 3 u ² . u’ |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= |
y
‘ = |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= |
y
‘ = |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
Autres
dérivées. |
Fonction ; « f ( x) » |
Dérivée : « f ‘( x) » |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
y
=Sin x |
Cos
x |
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
=Cos x |
-
sin x |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y
= Tan . x |
|
|
|
|||||||
|
|
|
|
||||||||||
|
|
Exemples : Calculer
les dérivées des fonctions suivantes : |
|
||||||||||
|
N°1 |
«
f ( x) »
= 3 x 4 + 2 x² + 3 x + 4 |
|||||||||||
|
|
«
f ‘( x) »
= 4 fois
3 4-1 + 2 fois 2 x 2-1 + 3 |
f ‘( x) = 12 x 3 + x + 3 |
||||||||||
|
N°2 |
«
f ( x) »
= ( x – 1 ) 3 ( x +
2 ) 4
; |
|
||||||||||
|
|
est
de la forme u . v = u ‘
v + u v ‘ |
|
||||||||||
|
|
Calcul
de « u ‘ » |
|
||||||||||
|
|
U = ( x – 1 ) 3 , ou
U = Donc
u’ = 3 |
|
||||||||||
|
|
Calcul
de « v ‘ » |
|
||||||||||
|
|
V = ( x + 2 ) 4 ;
ou V = v 4 avec v = x + 2 |
|
||||||||||
|
|
Donc
V ’ = 4 v3 v ’ =
4 ( x + 2 ) 3 ; car v ’ = 1
|
|
||||||||||
|
|
|
|
||||||||||
|
|
On a alors : y ‘
= f ‘( x) = U V’ + V U’ |
|
||||||||||
|
|
|
|
||||||||||
|
|
U V’ + V U’
= ( x – 1 ) 3 fois 4 ( x + 2 ) 3 + ( x + 2 ) 4 fois 3 (
x – 1 ) ² |
|
||||||||||
|
|
= ( x – 1 ) ² ( x + 2 ) 3
[ 4 ( x – 1 ) + 3 ( x + 2 ) ] |
|
||||||||||
|
|
y ‘ = ( x
– 1 ) ² ( x + 2 ) 3 ( 7 x + 2 ) |
|
||||||||||
|
|
|
|
||||||||||
|
|
·
Signe de la dérivée et sens de variation de la fonction. |
|
||||||||||
|
|
Suivant le signe de la dérivée, on peut
déterminer le sens de variation d’une fonction : - Si
la dérivée est nulle , la fonction est constante. - Si
la dérivée est positive dans un intervalle
] a , b [ , la fonction est croissante dans
cet intervalle. - Si
la dérivée est négative dans un
intervalle ] a ,
b [ , la fonction est décroissante dans cet intervalle. |
|||||||||||
|
|
|
|||||||||||
|
|
Exemple
1 : Construire le tableau de variation de la
fonction f(x) = |
|||||||||||
|
|
Info : f(x) = |
|||||||||||
|
|
Calculs des dérivées des termes
u et v :, u’ = 2
; et v ’ = -1 |
|||||||||||
|
|
Calcul de la dérivée de la fonction : f ‘ (x) = |
|||||||||||
|
|
5
> 0 et ( 1- x )² |
|||||||||||
|
|
|
|||||||||||
|
|
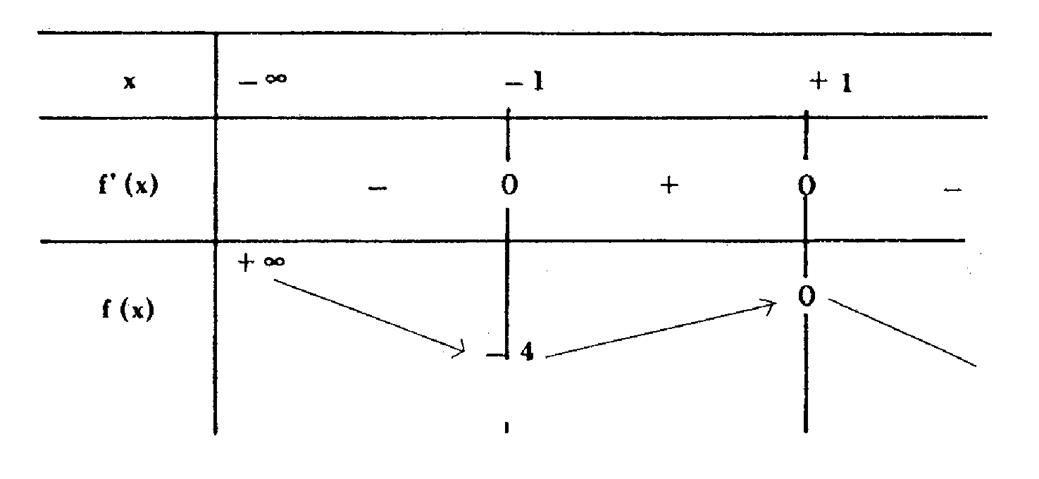
Exemple 2 : Construire le tableau de variation de la
fonction f (x) = - x 3 + 3 x – 2 |
|||||||||||
|
|
Calcul de la dérivée de la fonction :
f ‘ (x) = - 3 x² + 3 ; f ‘ (x)
est de la forme ax² + bx + c ; nous
devons calculer le discriminant ( |
|||||||||||
|
|
On pose : - 3 x² + 3 = 0 |
|||||||||||
|
|
|
|||||||||||
|
|
|
|
||||||||||
|
|
Dans le cas d’une dérivée de la forme ax² +
bx + c , elle admet 2 solutions pour f ‘ (x) = 0 , la
dérivée est : - « négative »
entre les racines si a > 0 - « positive » entre les racines si a
< 0 |
|||||||||||
|
|
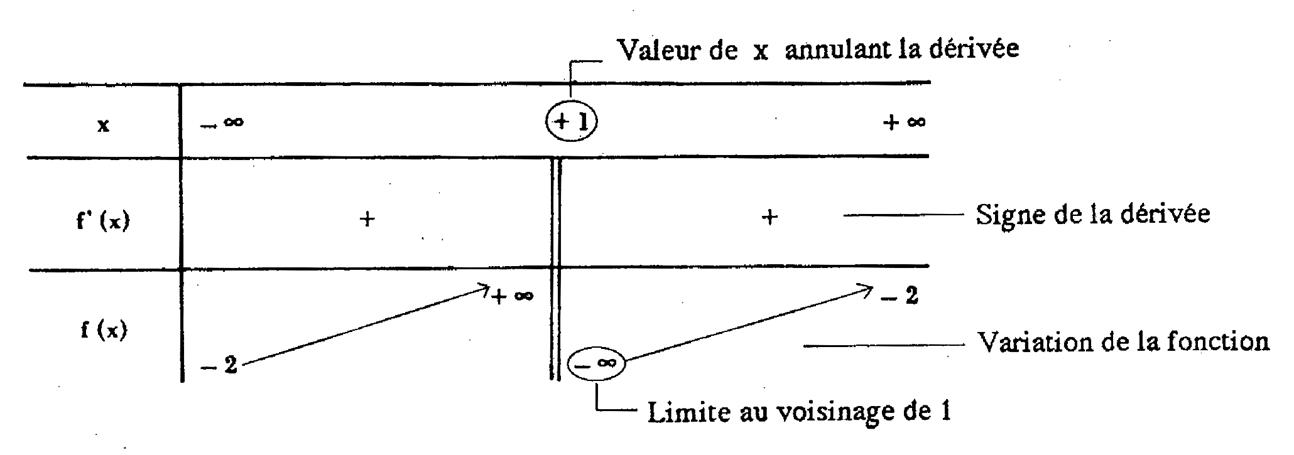
Soit
le tableau de variation : |
|||||||||||
|
|
||||||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
||||||||||
|
|
TRAVAUX AUTO FORMATIFS. |
|||||||||||
|
|
|
|
||||||||||
|
|
CONTROLE |
|
||||||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
|
EVALUATION :
|
|||||||||||
|
|
|
|
||||||||||
|
|
Calculer
les fonctions dérivées des fonctions suivantes : |
|||||||||||
|
|
|
|
||||||||||
|
|
a)
f (x) = |
|
||||||||||
|
|
|
|
||||||||||
|
|
b) f (x) =
|
|
||||||||||
|
|
|
|
||||||||||
|
|
c) f (x) =
|
|
||||||||||
|
|
|
|
||||||||||
|
|
Faire le tableau de variation et tracer la
courbe représentative de la fonction : |
|||||||||||
|
|
|
|
||||||||||
|
|
f (x) =
|
|
||||||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||