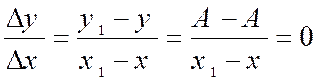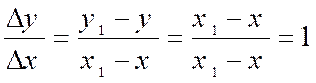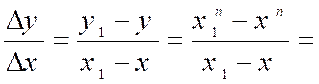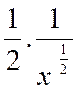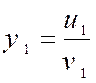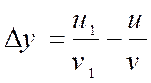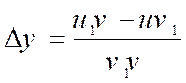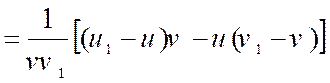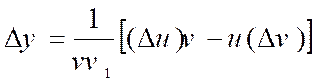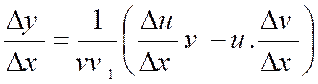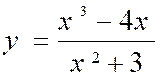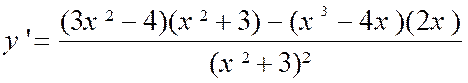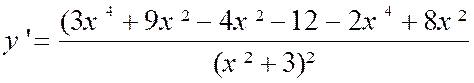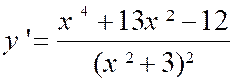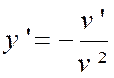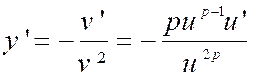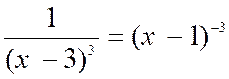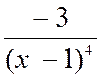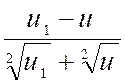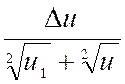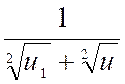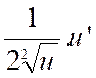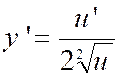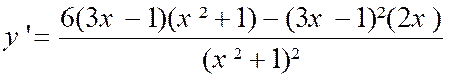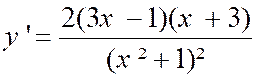Index warmaths
Liste des cours sur les « dérivées «  :		Vers aide individualisée
	CALCUL DES DÉRIVÉES
	Ce cours aborde les calculs des dérivées
	1 ) Dérivée d’une constante :
	2°) Dérivée de
	3°) Dérivée du monôme ^n
	4°) Dérivée d’ une somme
	5°) Dérivée d’ un produit ( Généralisation )
	6 °) Dérivée d’un polynôme
	7°) Dérivée d’un quotient
	8°) Dérivée de la fonction de la forme «  y = u ^m » ……………admet pour dérivée « y’ = u ^m-1 u’ »
	9°) Application de la dérivée de la forme «  y = u ^m » : soit Dérivée d’une racine carrée .

(1)	Dérivée d’une constante : y = A
	Quel que soit « x », on a y = A, donc
	Donc	Lim			= 0
						Soit y' = 0
	Une fonction constante admet en tout point une dérivée nulle.

2 -	Dérivée de
	Quel que soit « x », on a :y = A, donc
	Donc	Lim			= 1
						Soit y' = 1
	Une fonction «  y = x » admet en tout point une dérivée égale à 1

(3)	Dérivée du monôme ^n
	Quel que soit « x », on a : y = A, donc
	Lorsque tend vers 0 , « 1 » tend vers «  » et chacun des «  » termes du dernier membre a pour limite ^n-1
	Donc	Lim			= n x ^n-1
	Le monôme «  y = x^n » admet en tout point une dérivée égale à
	On voit ainsi que les fonctions  :
	«  »  … « »  ; …..admet pour dérivée : « 1 »
	Calcul :  ; soit ;
	= « x » ; admet pour dérivée : « 1 » ; « x² » ; admet pour dérivée : « 2x » ; « x^3 » admet pour dérivée : « 3 x² » ; « x^4 » admet pour dérivée : « 4 x ^3 » ; …………….
	Voir ci-dessous la racine carrée de «  » : qui s’écrit « x »

3 -	Dérivée d’ une somme :
	Soient u(x) ; v(x) ; w(x) des fonctions de « x » admettant pour dérivées respectives : u ‘ (x) ; v ‘ (x) ; w ‘ (x)
	Lorsque « x » prend la valeur « x1 » , la somme «  y = u + v + w » prend la valeur «  y1 = u1 + v1 + w1 » et l’on obtient en retranchant terme à terme : y = y1 – y = ( u1 – u ) + ( v1 – v) + ( w1 – w) = u + v + w . soit + + Lorsque tend vers 0 , u’ ; v’ ; w’

Donc	Lim

La somme de plusieurs fonctions dérivables admet pour dérivée la somme des dérivées de chacune de ces fonctions.
	y = u + v + w		y' = u’ + v’ + w’
Autrement dit une somme se dérive terme à terme.

4 -	Dérivée d’ un produit :
	1°) Soient u(x) ; v(x) ; deux fonctions de « x » admettant respectivement pour dérivées respectives : u ‘ (x) et v ‘ (x) .
	Lorsque « x » prend la valeur « x1 » , le produit «  y = u v  » prend la valeur «  y1 = u1 v1  » et l’on peut écrire . : y = y1 – y = ( u1 v1 ) – (u v) = ( u1 v1 – u v1 ) + ( u v1 – u v ) = ( u1 – u ) v1 + ( v1 – v ) u soit = u . v1 + u . v et . v1 + u. Lorsque tend vers 0 , v1 v ; u’ ; v’ et on obtient ( info ++)

Donc	Lim

Le produit de deux fonctions dérivables admet pour dérivée «  y ’ = u ‘ v + u v ‘ »
2°) Généralisation :
Si «  y = u v w » on obtient :
«
					Y’ = u’ v w
Cette démonstration s’étend par récurrence à un nombre quelconque de facteurs. Le produit de plusieurs fonctions dérivables admet pour dérivée la somme des expressions obtenues en remplaçant successivement dans ce produit , chaque fonction par sa dérivée.
Corollaire :
Si on multiplie une fonction dérivable par une constante sa dérivée est multipliée par cette constante.

	Si «  » , on obtient «  » voir (1) ; la dérivée de «  » se réduit à « » ; donc
	Ainsi d’après ( 2) on obtient la dérivée du monôme «  A x^n »
		y = A x^n		y ’ = n A x^n-1
5 )	Dérivée d’un polynôme :
	Un polynôme de degré « m » admet pour dérivée un polynôme de degré «  m – 1 »
	Ainsi la dérivée du polynôme : «  f (x) = A m x ^m + A m-1 x ^m-1 + A m-2 x ^m-2 + …..+ A 1 x ^1 + A 0 »
	Est la somme des dérivées de chacun de ses termes.
	«  f ‘(x) = m A m x ^m-1 + ( m -1) A m-1 x ^m-2 + …..+ 2A 2 x ^1 + A 1 »
	Ainsi : (par exemples)
		«   »	Admet pour dérivée..	«   »
		«  y = a x² + bx + c  »	Admet pour dérivée..	«   »
		«  y = x^3 + p x + q  »	Admet pour dérivée..	«  y’ = 3x² + p  »
		«  y = ax^4 + p x² + q  »	Admet pour dérivée..	«  y’ = 4x^3 + 2px  »
	Cas particulier :
		«  y = x + b »	Admet pour dérivée..	«  y’ =  »	«  y’ =  »
					«  y’ =  »
	Nota : on sait que …				«  y’ =  »
					«  y’ =  »

6 )	Dérivée d’un quotient :
	Soient « u (x) » et « v(x) » deux fonctions de « x » dérivables sur un intervalles où « v(x) » Lorsque « x » prend la valeur « x1 » , la fonction «  » prend la valeur «  » et on peut écrire :
	=			Voir ci-dessus et
				On réduit les deux fractions au même dénominateur !!!
				Et : u1- u =  ; v1- v =
	Soit
	Et
	Lorsque	On remarque que :	a)	c)	b)
	Et l’on obtient :

Donc	Lim	=

En résumé :

	Le quotient de deux fonctions dérivables admet pour dérivée :
	Exemple : trouver la dérivée de s’écrit :
	Corollaires : 1°) la dérivée de est …………………………………
	Si « u = 1 » ,( alors « u’ = 0) la dérivée de se réduit à
	Donc :
	En particulier
	2°) 0n peut utiliser la formule précédente pour calculer la dérivée de sous la forme du produit : u . v .  ; on obtient :
	3°) Remarque : autre façon de trouver la dérivée de ( voir le monôme)
	s’écrit sous la forme y = x^-1 donc y ’ = -1 x^-1-1 ; y’ = -1 x^-2					D’ où y’ = -1 on retrouve :
	Dérivée d’une puissance entière :
	Soit u (x) une fonction de « x » admettant pour dérivée « u’ (x) » . La fonction « y= u ^m » peut être considérée comme un produit de « m » facteurs : « y = u .u .u …. ».
	Elle admet pour dérivée la somme « m » termes égaux à «  u ^m-1 u’ »
7 )	La fonction «  y = u ^m » admet pour dérivée « y’ = u ^m-1 u’ »
	On vérifie que la dérivée «  y = u ^m » est  « y’ = u ^m-1 u’ »
	Remarque : La règle précédente s’applique également lorsque « m » est un entier négatif . Posons « m = - p » et « y = u^m » qui devient « y = u ^- p » = =  ; on obtient
	= - p u ^–p-1u’ soit « y’= mu^m-1 u’ »
	Ainsi , par exemple : « y =  » admet pour dérivée : « y ‘ = - 3 ( x-1)^-4 =
8 )	Dérivée d’une racine carrée :
	Soit « u(x) » une fonction positive de « x » admettant pour dérivée « u’ » et soit « y =  »
	On obtient : = = =
	D’où : = .
	Lorsque « x1 » tend vers « x » , « u1 » tend vers « u » et tend vers « u’ » ; le rapport admet donc pour limite :
	La fonction « y =  » admet donc dérivée  :
		y =
	Exemple de calcul de dérivée.
	Soit à calculer la dérivée de la fonction « y=  »
	Cette fonction est de la forme « y=  » avec « u » = (3x-1)² et « v » = (x²+1)
	Or «  u = w² » et « u’= 2 w » ; « w ’= 2 ( 3x – 1) fois 3 » = « 6 ( 3x -1) » et « v ’ = 2 x »
	On obtient : = Soit après réduction :
	Il y a intérêt, tout au moins au début, à utiliser des fonctions intermédiaires de façon à se ramener à des types connus.
	Voir le résumé ..sur le tableau :