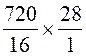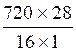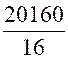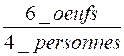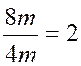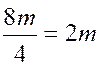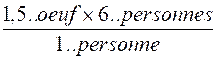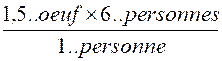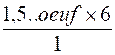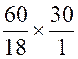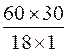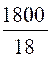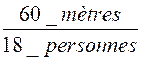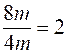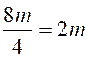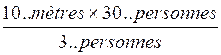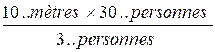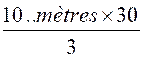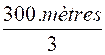Pré requis:

Fraction nomenclature
Fraction équivalente
Prendre une fraction d’un nombre
Produit en croix

ENVIRONNEMENT du dossier :

Index warmaths

Objectif précédent : 1°) la règle de trois (informations) 2°) activités pré requises. 3°) notion abordée au collège ( 6^ème)

Objectif suivant : 1°)La quatrième proportionnelle 2°)les grandeurs proportionnelles 3°) la fonction linéaire

Tableau 166

DOSSIER : "la REGLE de TROIS "

TEST

COURS

Devoir Contrôle

Devoir évaluation

Fiches …Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

Notion de la règle de Trois :

Il existe de nombreuses relations qui se calculent uniquement au moyen de la multiplication et de divisions successives ; ainsi ; par exemple ; j’ai acheté 15 bouteilles pour 120 € , je veux savoir combien me coûteront 40 bouteilles ; ou bien j’ai gagné 240 € en travaillant 6 jours et je veux savoir combien on me payera en un mois de 25 jours de travail ;ou encore 5 000 € m’ont rapporté 300 € en un an et je veux savoir combien me rapporterait dans le triple de temps une somme de 30 000 € .

Dans tous les cas le raisonnement est le même ; je cherche le résultat pour une unité , puis je le multiplie par le nombre d’unités .

Dans tous les exemples précédents , les grandeurs sont dit « directement proportionnelles » mais il y a des cas où la relation est inverse ; ainsi : plus j’emploie d’ouvriers à un travail , moins de temps il faudra pour le finir . Plus un mur est haut , ou épais , moins de longueur on ne pourra en faire dans un temps déterminé ou avec une quantité de matériaux donnée , on dit dans ce cas , que la règle de trois est inverse , car les quantités sont inversement proportionnelles .

La règle de trois est simple lorsque le problème se réduit à une seule relation ; et elle est composée lorsque le problème comprend une série plus ou moins longue de rapports .

Elle est directe ou inverse selon que les quantités sont directement ou inversement proportionnelles à la quantité demandée.

La règle de trois composée peut avoir à résoudre les combinaisons les plus diverses de quantités directement et inversement proportionnelles .

La Règle de Trois

Règle de trois : la règle de trois simple à pour objet de fournir le terme inconnu d’une proportion dont les trois autres termes sont donnés.

La règle de trois est un "procédé" de calcul permettant d ' étudier la variation de deux grandeurs proportionnelles.

La règle de trois s ’ applique à la forme mathématique : 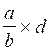=  ? (= c )

Voir: La multiplication d'un nombre ( ou grandeur) par une fraction

Ce qui donne le modèle : 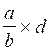(qui ne se calcule pas ) devient le produit 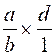qui lui peut se calculer pour devenir le calcul : 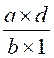devient après calcul

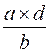
si le résultat est appelé « c » alors 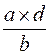= c

Cette écriture peut et doit se transformer sous la forme =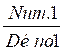

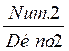
pour donner l'égalité* : = ;

* l ‘ égalité est vraie si : ad = bc

Nous obtenons le produit « en croix » suivant : ( SOS cours)

a d = c b

Conclusion : la "règle de trois" est une transformation du "produit en croix" ,pour régler la recherche d'une quatrième grandeur (appelée "quatrième proportionnelle" ).

CALCULS PARTICULIERS

Forme : « une fraction est égale à un nombre » : = c ; on recherche ou « a » ou « b »

Alors faire la transformation :

= est effectuer le produit en croix .tel que : a 1 = c b ;soit : a = c b

ou = devient = b ;pour obtenir b =

Interdisciplinarité:

Enoncé : Calculer 8 pour cent de 250

Pour en savoir plus : Voir : les pourcentages

On sait que 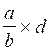=  ? (= c )

Donc : =  c

c = 20

Enoncé n°1 :

Sachant que 16 m de tissu ont été payés 720 € ,trouvez le prix de 28m.

Résolution :

Le prix étant proportionnel à la longueur , le prix cherché est :

28 = 1 260 €

= = = 1 260

au lieu d'utiliser les fractions , on peut employer la méthode de "réduction à l'unité". Le prix du mètre de tissu est de soit 45 € .

Le prix de 28 m est de 45 28 = 1260 €

Enoncé n° 2 :

Sachant que pour faire un gâteau de 4 personnes six œufs ,combien faut-il d'œufs pour faire un gâteau de 6 personnes ?

Résolution :

Le nombre d'œufs étant proportionnel au nombres de personnes , le prix nombre d'œufs cherché est :

6 = 9 œufs

Explication du calcul:

= = = 9

Au lieu d'utiliser les fractions , on peut employer la méthode de "réduction à l'unité". Le nombre d'œufs par personne est de soit 1,5 œuf pour 1 personne.

Le nombre d'œufs pour 6 personnes est de 1,5 6 = 9 œufs

A propos des unitésL qui s' annulent par la division:

les unités de même "famille" s ' 'annulent dans la division:

exemple : alors que ,il en est ainsi avec toutes les grandeurs.

= après simplification : ; soit : = 9 œufs

Enoncé n°3 :

Un entrepreneur fait construire d ' habitude une maison en 60 jours avec 15 ouvriers .six personnes tombent malades, déterminer la durée des travaux .

Il n ' y a pas de proportionnalité : le travail de l'ensemble des personnes ne peut se réduire au travail d'un seul individu .

Résolution :

La durée des travaux étant proportionnel aux nombres de personnes , la durée cherchée est :

? = Problème : le nombre de jours de travail n'a rien de proportionnel .

Le nombre de jours est constant : 6015 est = 900

Il y a 15 - 6 = 9 ouvriers pour effectuer les 900 jours de travail

Conclusion: 900 : 9 =100 ; il faudra 100 jours pour construire la maison.

Enoncé N° 4:

18 ouvriers ont fait , dans des conditions déterminées , 60 mètres d'ouvrage. Combien 30 ouvriers feraient-ils de mètres du même ouvrage, toutes les autres conditions restant les mêmes ?

Résolution :

Les deux grandeurs sont directement proportionnelles .

Le nombre de mètres construit étant proportionnel au nombres de personnes , le nombre de mètres cherchés est :

30 = 100 mètres

Explication du calcul:

= = = 100

Au lieu d'utiliser les fractions , on peut employer la méthode de "réduction à l'unité". Le nombre de mètre par personne est de soit 10/3 mètres pour 1 personne.

Le nombre de mètres pour 30 personnes est de 10/3 30 = 100 mètres

A propos des unitésL qui s' annulent par la division:

les unités de même "famille" s ' 'annulent dans la division:

exemple: alors que , il en est ainsi avec toutes les grandeurs.

= après simplification :

soit : = = 100 mètres

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1 ° ) Enoncer la procédure permettant d’effectuer « la règle de trois ».

EVALUATION:

Rechercher la quatrième proportionnelle :

On dirait aussi : Transformer , par le produit en croix , les fractions équivalentes :

=

=

=

=

et encore :

a) = 5 b) = 7 ;

Enoncé 1: Sachant que 16 m de tissu ont été payés 720 € ,trouvez le prix de 28m.

Enoncé 2: Sachant que pour faire un gâteau de 4 personnes six œufs ,combien faut-il d'œufs pour faire un gâteau de 6 personnes ?

Enoncé 3: Un entrepreneur fait construire d ' habitude une maison en 60 jours avec 15 ouvriers .six personnes tombent malades, déterminer la durée des travaux .

Il n ' y a pas de proportionnalité : le travail de l'ensemble des personnes ne peut se réduire au travail d'un seul individu .

Enoncé N° 4: 18 ouvriers ont fait , dans des conditions déterminées , 60 mètres d'ouvrage. Combien 30 ouvriers feraient-ils de mètres du même ouvrage, toutes les autres conditions restant les mêmes ?

CORRIGE :

Transformer , par le produit en croix , les fractions équivalentes :

=	5x =36	=	35=3x	=	7x =36	=	35=12x
	X= 7,2		X = 35/3		X=36/7		X=35/12

a) Résoudre = 5 solution :	b) Résoudre = 7 ; solution :
= 5 devient =	= 7  devient =
x = 5 fois 13 x = 65	13 fois 1 = 7 fois x 13 =7 x 13/7 = x ou x = 13/7