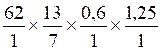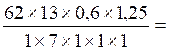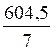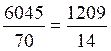Pré requis :
|
Opérations avec les décimaux relatifs présentation |
|
|
Addition avec les
décimaux relatifs |
|
|
Soustraction avec les décimaux relatifs |
|
|
Multiplication
avec les décimaux relatifs |
|
|
Division avec les
décimaux relatifs |
|
|
Fractions se
ramenant à un nombre décimal |
ENVIRONNEMENT du
dossier :
|
|
|
|
|
DOSSIER :CALCUL
NUMERIQUE et Algébrique : Chaînes d ' opérations se ramenant à la
somme de deux nombres relatifs de signe contraire.
Niveau 3 /6: l'expression ne
contient pas de parenthèses.
|
COURS
|
Interdisciplinarité |
|
OBJECTIF : PRIOCAL :
Cet objectif aborde les priorités dans
le calcul à effectuer dans une chaîne
d’opérations.( ou expressions algébriques )
Remarque: on ne sait "traiter"
que deux nombres à la fois.
Remarque 1
Les expressions algébriques
contiennent une suite d’opérations , elles ne
contiennent pas de parenthèses .
Remarques 2 : un nombre relatif s’appelle
« nombre algébrique » d’où : un calcul algébrique est un calcul
dont le résultat doit être un nombre relatif ……..
Info COURS :
Les expressions ne contiennent pas de parenthèses :
exemple : «
8 + 56 + 12 + 965,12 »
procédure:
|
Faire dans
l’ordre : |
exemple : « 8 + 56 + 12 + 965,12 » |
|
1 )
transformer « l’expression » en « somme » de
nombres relatifs |
x = «
(+8)+( + 56) + (+12) +(+ 965,12) » |
|
2 ) faire la somme des nombres de
même signe |
x = (+(8
+ 56+12 + 965,12) = |
|
3°) Rendre
compte |
x = (+1041,12) |

Cas II ( 2 types de difficultés)
il
faut transformer « l ’ expression algébrique
» en « somme algébrique »
|
Voir l ‘ objectif :
Expression et Somme algébrique |
|
Attention au signe du premier
nombre : s ’
il est négatif : faire la somme des
nombres négatifs s’il est positif : faire la somme des nombres négatifs ;
terminer par la somme de deux nombres
de signe contraire; |
A ) :
l’expression débute par un signe
« - » et ne contient que des signes « moins » .
exemple
« -12 - 56 - 4 - 5,7 »
procédure:
|
Il faut
faire dans l’ordre : |
Exemple: x
= -12 - 56 - 4-5,7 |
|
1 )
transformer « l’expression » en « somme » de
nombres relatifs(SOS cours) |
x = (-12) + (- 56) + (- 4) + (- 5,7) |
|
2 ) faire la
somme des nombres de même signe (ici moins) (SOS
cours) |
x = (- (12 + 56
+ 4 + 5,7 ) |
|
3 ° ) Rendre compte |
-12 - 56 - 4 -
5,7 = (-77,7) |
.
B ) : l’expression n’a pas de signe en tête d’expression ou elle
débute par un signe « + » et ne contient que des signes « moins » .
exemple
« 12- 56 - 4-5,7 »
ou « +12 - 56 - 4-5,7 »
procédure:
|
Il faut faire dans l’ordre : |
Exemple: x =
12-56-4-5,7 |
|
1 )
transformer « l’expression » en « somme » de
nombres relatifs(SOS cours) |
x = (+12) + (- 56) + (- 4) + (- 5,7) |
|
2 ) faire la
somme des nombres de même signe (ici moins) (SOS
cours) |
(- (56
+ 4 + 5,7 ) soit : ( - 55,7 ) |
|
3°) faire
la somme des nombres de signe contraire . |
x = (+12) + (- 55,7) = ( - ( 55,7 - 12
) = ( - 33,7 ) |
|
3 ° ) Rendre compte |
12- 56 - 4-5,7 = ( - 33,7 ) |
Cas III
l’expression ne contient que des « additions » et des
« soustractions » .
voir le cas
précédent « 12- 56 - 4 - 5,7 »
Exemple : x = - 12 + 56 - 4 +
5,7
Procédure :
|
Il faut faire dans
l’ordre : |
|
|
1 ) transformer « l’expression » en
« somme » de nombres relatifs |
x = (-12) + (+56) +
(-4) + (+5,7) |
|
2 ) regrouper les nombres de même signe |
(-12) ; (-4) et (+5,7) ;(+56) |
|
3 ) puis faire la somme des deux nombres de
signes contraires.* |
(-(12+ 4 ))= ( -16) Somme
des Valeurs absolues des nombres négatifs |
|
(+(56 + 5,7 ))= ( +61,7) Somme
des Valeurs absolues des nombres positifs |
|
|
4) faire l'addition des
deux sommes calculées (nombres de signes contraires) |
x = (-16 ) + (+ 61,7 ) x = (+ ( 61,7 - 16 ) ) x = (+ 45,7 ) |
|
5°) Rendre compte |
x = -12+56-4+5,7 ; x = (+
45,7 ) |
.
Cas IV :l’expression contient des multiplications: (exemple :calcul d’un volume)
a
) Il n’y a que des multiplications:
sans signe négatif :
exemple ( 9![]() 1,2
1,2 ![]() 6,9 )
6,9 )
Procédure:
il faut faire le produit
des nombres ( ou valeurs absolues)
|
Il faut faire : |
|
|
1ère
multiplication : |
9 |
|
2ème
multiplication |
10,8 |
|
Rendre compte |
9 |
a)
 Il n’y
a que des multiplications:
avec un ou des signes
négatifs :
Il n’y
a que des multiplications:
avec un ou des signes
négatifs :
exemple : ( - 9![]() 1,2
1,2 ![]() 6,9 ) ; ( - 9
6,9 ) ; ( - 9![]() - 1,2
- 1,2 ![]() 6,9 ) ; ( - 9
6,9 ) ; ( - 9![]() -1,2
-1,2 ![]() -6,9 )
-6,9 )
procédure: il faut faire le produit
des nombres ( ou valeurs absolues)
|
Il faut faire : |
|
|
1ère
multiplication : |
9 |
|
2ème
multiplication |
10,8 |
Pour le résultat final :
 - si la suite de multiplications à 1 ou 3 ; 5 ; 7 signes « moins » : le résultat sera du
signe « moins »
- si la suite de multiplications à 1 ou 3 ; 5 ; 7 signes « moins » : le résultat sera du
signe « moins »
exemples :
(
- 9![]() 1,2
1,2 ![]() 6,9 ) = -74,52
6,9 ) = -74,52
(
- 9![]() -1,2
-1,2 ![]() -6,9 ) = -74,52
-6,9 ) = -74,52
-
 si la suite de multiplications à
2 ; 4 ; 6 ; 8 ;…signes « moins » : le
résultat sera du signe « plus » .
si la suite de multiplications à
2 ; 4 ; 6 ; 8 ;…signes « moins » : le
résultat sera du signe « plus » .
exemples :
( - 9![]() - 1,2
- 1,2 ![]() 6,9 ) = +74,52
6,9 ) = +74,52
( - 9![]() -1,2
-1,2 ![]() -6,9
-6,9 ![]() - 2 )
= + 149,04
- 2 )
= + 149,04
a)
la suite de multiplication ne contient que des nombres de
signe négatif :
exemple (-9![]() -1,2
-1,2 ![]() -6,9 )
-6,9 )
procédure : calculer
le produit des valeurs absolues ; compter le nombre de nombres
.
si le nombre de nombres
est pair : le produit est un nombre
relatif positif .
si le nombre de nombres
est impaire : le produit est un nombre relatif négatif .
Cas V :la suite d’opérations ne contient que des divisions .( très rare)
exemple : 15 : 8 :2
procédure
|
il faut commencer par la division de gauche. |
||
|
1ère
division : 15 :
8 |
1,875 |
|
|
2éme
division : 1,875 : 2 |
0,9375 |
|
|
Rendre compte |
15 : 8 :2 = 0,9375 |
|
Exemple : avec des
fractions
Procédure:
-
vous avez travailler le cours sur les opérations sur les fractions , alors vous avez
une première réponse.
-
Vous n’avez pas travaillé le cours sur les
fractions « opérations » alors faire comme il suit :
|
Le plus simple est
d’écrire les fractions sous forme d’une division : |
|
|
|
il faut commencer par la division de gauche. |
|
( |
(13 : 7) : 1,2 =
2,6 : 1,2 = 2,1666667
; SOS cours |
|
( |
(13 :5) : ( 27 :8) =
2,6 : 3,375 = 0,7703703
; SOS cours |
|
( |
[ (13 :5) : (
27 : 8)] : 1,2 = ( 2,6 :
3,375 ) : 1,2 = 0,7703703 : 1,2
= 0,6419752 ; SOS cours |
Cas VI : suite d’opérations contenant que
des « multiplications » et des « divisions »
A) : La
division "tombe juste", la division représente un nombre décimal . SOS cours ![]()
Exemple 1: ( 62![]() 16 : 5
16 : 5![]() 1,2)
1,2)
|
procédure: |
Exemple : ( 62 |
|
1 ° )
faire la (ou les division) : 16 : 5 = 3,2 |
( 62 |
|
2° )
Faire les multiplications :il n ' y a
pas d’ordre impératif à respecter ;
mais il est conseillé de faire les opérations en partant de la gauche, |
198,4 fois 1,2 = 238,08 |
|
Rendre compte : |
:( 62 |
|
Cas 2 : la chaîne contient des "fractions ou
écritures fractionnaires" |
|
|
Une
division "ne tombe pas
juste" ;on dit aussi " la (ou les)division
ne représente pas un nombre décimal ." |
Exemple 1:( 62 |
|
procédure: |
|
|
Mettre la (ou les )
fraction sous forme d ‘une
fraction irréductible SOS cours |
|
|
Mettre tous les autres nombres sous forme de
fraction de dénominateur égal à 1 |
|
|
Faire le produit des numérateurs sur le
produit des dénominateurs |
|
|
laisser le résultat
sous forme fractionnaire ,puis rendre irréductible
la fraction SOS
cours ou donner une
écriture décimale .
|
|
Cas VII : la suite
d’opérations contient des
additions, soustractions ,multiplications
,divisions: exemple -8,4 + 11![]() 2 +
2 +![]() =
=
|
Procédure : faire
dans l ‘ordre |
Exemple : -8,4
+ 11 |
|
1 ° ) Faire la (ou les ) division : 13 : 5 = 2,6 |
-8,4 + 11 |
|
2°) faire la ( ou les )
multiplication |
-8,4 + 22 +2,6 = |
|
3° ) transformer « l’expression » en
« somme » de nombres relatifs |
(-8,4
)+( + 22) + (+2,6) = |
|
4° ) faire les
sommes des nombres de même
signe . (peu importe l’ordre) somme des positifs et somme des négatifs . |
( + 22) + (+2,6) = ( +
(22+2,6))=(+24,6) il n’y a qu’un nombre négatif : (-8,4 ) |
|
5° ) puis faire la somme des deux nombres de
signes contraires.* |
(+24,6)+ (-8,4 ) = ( + (24,6 –8,4)) |
|
= (+16,2) |
|
|
|
|
|
6° ) Rendre compte |
-8,4 + 11 |
Cas VIII : l’expression contient des
additions, soustractions ,multiplications
,divisions , des puissances: Exemple 3, 52- 9 : 2 + 4![]() 92 =
92 =
|
Procédure , faire dans
l ‘ordre : |
3, 52- 9 : 2
+ 4 |
|
1° ) les puissances |
11,25 - 9 : 2 + 4 |
|
2 ° ) Faire la (ou
les ) division |
11,25 – 4,5 + 4 |
|
3° ) faire la ( ou les )
multiplication |
11,25 – 4,5 + 324 = |
|
4° ) transformer
« l’expression » en « somme » de nombres relatifs |
(+11,25) +( – 4,5)+ (+ 324) = |
|
5° ) faire les
sommes des nombres de même
signe . (peu importe l’ordre) a) somme des positifs : b) somme des négatifs : |
a) (+11,25) + (+ 324) =(+335,25) b) ( – 4,5) |
|
6° ) puis faire la somme des deux nombres de
signes contraires.* |
(+335,25)+( – 4,5) |
|
(330,25) |
|
|
|
|
|
7° ) Rendre compte |
3, 52- 9 : 2
+ 4 |
Cas X : Cas GENERAL :
l’expression contient
des additions, soustractions
,multiplications ,divisions (ou fractions….) , des puissances , des
racines:
exemple 9,2 - 42 ![]() 7 + 2,7
7 + 2,7 ![]() (-6)2
+
(-6)2
+ ![]() -
- ![]() =
=
|
Procédure à suivre : |
Exemple: 9,2 - 42 |
|
1° )
faire la racine : au préalable faire le calcul sous la racine
au cas où….. |
9,2 - 42 |
|
2°) faire les
puissances |
9,2 - 16 |
|
3°)faire
les divisions |
9,2 - 16 |
|
4°)faire
les multiplications |
9,2 - 112 + (+ 97,2 )
+ 5
- 20 |
|
5°) Transformer
l’expression algébrique en somme algébrique |
(+9,2)+( - 112) + (+ 97,2 ) + (+ 5) + ( - 20) |
|
6°)faire
la somme des nombres positifs |
(+9,2)+ (+ 97,2 ) + (+ 5) = (+(9,2+97,2+5)= (+ 111,4) |
|
7°) faire la somme des
nombres négatifs |
( - 112) + ( - 20) =( -
(112+20)) = (-132) |
|
8°) faire la somme des
nombres de signe contraire. |
(+ 111,4)+ (-132) = ( - (132-
111,4)) = (-20,6) |
|
9°) Rendre compte |
9,2 - 42 |
CONTROLE: et ou PREPARATION devoir
Dans quel ordre doit-on
effectuer les opérations ,dans une chaîne d’opérations contenant:
1°) Dans quel ordre
doit-on effectuer les opérations ,dans une chaîne d’opérations contenant:
que des additions?
|
Procédure : |
exemple : « 8 + 56 + 12 + 965,12 » |
2° )
Dans quel ordre doit-on effectuer les opérations ,dans une chaîne d’opérations contenant:
Que des soustractions ?
.
|
procédure |
Exemple: x =
-12-56-4-5,7 |
3° )
Dans quel ordre doit-on effectuer les opérations ,dans une chaîne d’opérations contenant:
Que des additions et des soustractions ?
|
procédure |
Exemple: x = -12+56-4+5,7
|
4°) Dans quel ordre doit-on
effectuer les opérations ,dans une chaîne d’opérations contenant:
Que des multiplications ?
5°) Dans quel ordre
doit-on effectuer les opérations ,dans une chaîne d’opérations contenant:
Que des divisions ?
6° ) et ou
des « multiplications » et des « divisions »
Cas 1 : La
division "tombe juste", la division représente un nombre décimal .
Cas 2 : La
chaîne contient des "fractions ou écritures fractionnaires"
7°) Dans quel ordre
doit-on effectuer les opérations ,dans une chaîne d’opérations contenant:
Que
des additions; des soustractions ;des
multiplications et des divisions (ou
fractions) ?
|
Procédure : faire
dans l ‘ordre |
exemple -8,4
+ 11 |
8° )
Dans quel ordre doit-on effectuer les opérations ,dans une chaîne d’opérations contenant:
Que des
additions, soustractions ,multiplications
,divisions , des puissances ?
|
Procédure à suivre : |
Exemple: 9,2 - 42 |
9 °)Que des additions,
soustractions ,multiplications ,divisions , des puissances et des racines
?
|
Procédure à suivre : |
Exemple: 9,2 - 42 |
EVALUATION
Faire les calculs
suivants en indiquant les étapes intermédiaires:
1°) 3 + 5,6 + 8
=
|
|
2° )-
5 - 6,3 -7,2 =
|
|
3° )-8,3
+ 5 - 9 - 13,5 + 7,7 =
|
|
4°) 15,3 - 4 ![]() 5,3 + 7
5,3 + 7![]() 3 =
3 =
|
|
5°) 3, 5 - 9 : 2 + 4![]() 9 =
9 =
|
|
6°) -8.4 + 11 +![]()
![]() 1,2 =
1,2 =
|
|
7 °) 3, 52- 9 : 2 + 4![]() 92 =
92 =
|
|
8 ° ) -8,42 + 11 +
(![]() ) 2
) 2![]() 1,2 =
1,2 =
|
|
9°)Que des additions,
soustractions ,multiplications ,divisions , des puissances et des racines
.