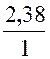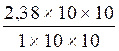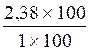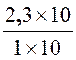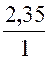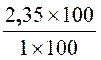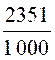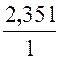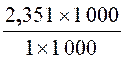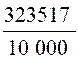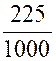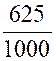Pré requis:
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier :
|
2°) savoir transformer un entier sous la forme d’une
fraction. |
2°) Savoir transformer une écriture
fractionnaire en fraction. 3°) Rendre irréductible une fraction décimale
(1) |
|
(46) DOSSIER : Transformer un nombre "D" en fraction
|
|
1°) Procédure permettant de transformer un nombre décimal sous la forme d’une
fraction décimale . |
|
|
|
|
|
|
|
|
|
|
COURS |
|
||||||
|
|
|
|
|
|
|
|
|
|
Définition
de l’objectif: Savoir représenter un
nombre décimal (exemple : 2,38) sous forme
de fraction: Par exemple : Il faut savoir passer de la forme « 2,38 » (nombre décimal) à
la forme de la
fraction : |
|
|
|
|
|
|
|
Rappel 1 : on appelle
« nombre décimal » le
quotient d’un nombre entier ( rationnel) par 10 ou
une puissance de 10 ; ( 10 1 ;
10 ² ; 10 3 ; …..) Dit
autrement : un nombre décimal est le résultat de la division d’un nombre
entier par « 10 » ou un multiple de 10 .(
100 ; 1 000 ; …..): Rappel 2 : On appelle
« fraction » : Dans
une fraction le numérateur et le dénominateur sont toujours des nombres entiers, si l’un de ses nombres
n ‘est pas un nombre
entier l’écriture ne s’appelle
plus « fraction » , on l’appelle
alors « écriture
fractionnaire . Dit
autrement : le groupe de deux nombres séparés par une barre de fraction
s’appelle « fraction » , ses
deux termes ( nombres ) sont
des nombres entiers. |
|
|
|
Procédure permettant de transformer un nombre décimal sous la forme d’une
fraction décimale : |
|
|
|
Pour
mettre un nombre décimal ( 2 ,38 )sous forme de fraction ( 1°) Il faut écrire le décimal ( 2,38) sous forme fractionnaire dont le numérateur est le nombre décimal donné et
dont le dénominateur vaut « 1 » .
2, 38 = 2°)
Il faut multiplier ,
à la fois , le numérateur et le
dénominateur par « 10 » (ou un multiple de dix ; 100 ;1000..........),afin
d’obtenir la fraction cherchée (le numérateur et le dénominateur sont deux
nombres entiers)
Remarques : On multiplie par « 10 » si le nombre
décimal à un seul chiffre après la virgule . On multiplie par « 100 » si le nombre
décimal à deux chiffres après la virgule . On multiplie par « 1 000 » si le nombre
décimal à trois chiffres après la
virgule ; Et ainsi de suite …….. . |
|
|
|
Exemples : |
|
|
|
· Mettre le nombre décimal « 2,3 » peut être représenté par la
fraction : |
|
|
|
2,3 = |
|
|
|
· Mettre le nombre décimal « 2,35 » peut être représenté par la
fraction : |
|
|
|
2,35 = |
|
|
|
· Mettre le nombre décimal « 2,351 » peut être représenté par la
fraction : |
|
|
|
2,351 = |
|
|
|
· Mettre le nombre décimal
« 32,3517 » peut être
représenté par la fraction : |
|
|
|
32 , 3517
= à vous de compléter !!! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* ces fractions peuvent peut être se simplifiées , jusqu’à ce qu’elles soient dites « irréductibles » , dans ce cas
il faut aller voir l’ objectif: « la fraction équivalente ». Rappel: une fraction a
toujours un nombre entier au
numérateur et un nombre entier
au dénominateur. |
|
|
|
|
|
|
Autres
exemples |
|||||||
|
0,5 = |
|
0,85 = |
|
0,225 = |
|
0,625 = |
|
|
0,4 = |
|
0,05 = |
|
1,6 = |
|
3,25 = |
|
|
|
PREPARATION ;( première partie) TRAVAUX AUTO FORMATIFS. Donner
la procédure permettant de transformer un nombre décimal en fraction décimale
? Série
1 : Ecrire les nombres décimaux suivants sous la
forme d’une fraction : 1.
Le nombre
décimal « 2,3 » peut être représenté par la
fraction : 2.
Le nombre décimal « 2,35 » peut être représenté par la
fraction : 3.
Le nombre
décimal « 2,351 » peut être représenté par la
fraction : 4.
Le nombre
décimal « 32,3517 » peut être représenté par la
fraction : |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Ecrire les nombres décimaux suivants sous forme
de fraction :(obligatoirement le numérateur et le dénominateur sont des
nombres entiers)
ALGEBRE :
|
|