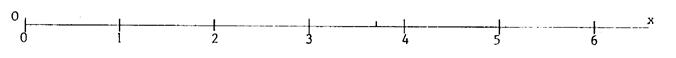Décembre 2012./12-12

Pré requis:

Notions préliminaires
«vocabulaire :  droite –demi- droite- segment »info ++		6^ème.

ENVIRONNEMENT du dossier:

Index « warmaths »

Objectif précédent : 1°) droite et courbe : vue en primaire. 2°) notions tracés élémentaires .. 3°) les droites –demi- droites -segments.

Objectif suivant : Les segments : mesure ; longueur ; et opérations.

Info 1 : Liste des cours en géométrie. Info 2 : Tableau Info 3 : la géométrie en arithmétique

FICHE de travaux : CORRIGE MESURE DES LONGUEURS.

Chapitres
	1°) Longueur de segments.
	2°) Mesurage de longueurs.
	3°) Encadrement d’une mesure
	4°) Graduation régulière. – Mesurage avec des nombres à virgule. ( nombre décimal)
TEST		COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité : Travaux dos.46	Corrigé Contrôle	Corrigé évaluation

Info COURS

Info. @

1°) Longueur de segments.

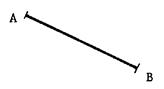
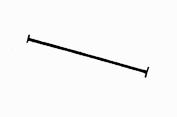
On vous donne trois segments ci-dessous  : Dont un référent , un [ A B ] et [ CD ] ; On vous demande avec votre compas ( balustre )et de « bloquer » ses branches sur l’écartement des extrémité du segment référent ; et de et de faire coïncider les extrémités « A » et « B » du segment [ A B ] , et d »en faire de même pour le segment [ CD ].

Question : avez-vous eu besoin de changer l’écartement des branches ? ( non) On peut dire qu’il y a le même écartement entre « A » et « B » qu’entre « C » et « D » . .

Remarque 1 : On aurait pu le constater d’une autre façon : Vous décalquez le segment référent ; et en sur [ A B ] et [ CD ]. Vous vous apercevez que le dessin du calque recouvre exactement [ A B ] et [ CD ].

Remarque 2 : une autre façon consisterait à couper la feuille entre les segments , on les superpose et on constaterait par transparence qu’ils coïncident .

Dans ces conditions : on dit que les segments sont superposables,

Autres activités :

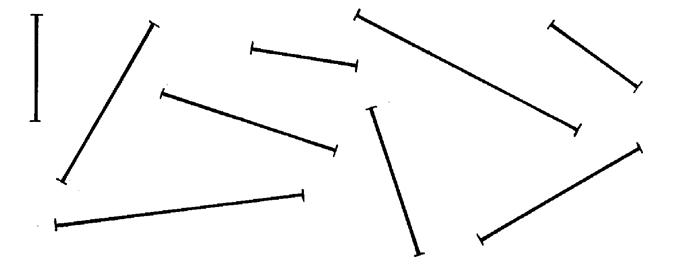
On vous propose , ci – dessous , 9 segments : dans un premier temps , nommez les extrémités. A l’aide de votre compas , ou du papier calque , cherchez les segments superposables .

On remarque que les segments superposables sont des segments qui ont la même longueur .

Mettre dans chaque case la liste des segments superposables.

Reprenons par exemple les segments [ A B ] et [ CD ] du début .

[ A B ] et [ CD ] sont superposables , donc il ont la même longueur .

On écrira : ( longueur [ A B ] ) = ( longueur [ CD ] )

La longueur de [ A B ] se note « AB »

On peut écrire : AB = CD

Info « notation »

Lorsque l’on rencontre l’écriture : AB = CD ; on doit lire : La longueur du segment AB est égale à la longueur du segment CD.

Info +++

2°) Mesurage des longueurs.

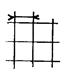
Il existe deux sortes de quadrillage de cahier ou copie scolaire.

u

U

Les petits carreaux :

Les gros carreaux :

En prenant « u » comme unité ( ou « U » ) pour mesurer une longueur on peux utiliser une feuille de cahier comme l’indique le dessin ci-dessous.

En regardant le dessin , on constate que «  AB = 7 u »

On dit aussi : avec l’unité « u » la mesure de la longueur est de [ A B ] = 7 et on écrit «  AB = 7 »

Si on écrit : AB = 7 u ; c’est une longueur Si on écrit : AB = 7 ; c’est une mesure de cette longueur ( avec l’unité « u »)

Activités :

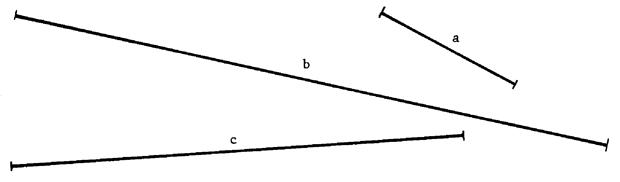
Avec les unités « u » ‘ « U » , cm , mm , mesurez les longueur « a » , « b » et « c » des segments ci – dessous et reportez ces nombres dans le tableau .

Unité

u

U

cm

mm

Longueur

a

b

c

Constatation : La mesure d’une longueur dépend de l’unité choisie. En particulier, si l’on change d’unité , en prenant un unité 10 fois plus petite, on obtient une mesure 10 fois plus petite.

ATTENTION : Les segments dont vous avez mesurer la longueur ont été donnés de telle sorte que les extrémités coïncident presque avec les graduations de votre instrument de mesure. Vous verrez qu’il n’en est pas toujours ainsi. En fait , dans tout mesurage , la valeur trouvée (nombre) est toujours une valeur « approchée » Au lieu d’écrire AB = 5 on devrait écrire : AB 5 ( ce qui se lit «  sensiblement égal à … » ou « est   voisin de … »

Info ++

3°) Encadrement d’une mesure.

On veux mesurer la longueur du segment [ C D ] ci-dessous avec l’unité « u » ( voir ci-dessus ) Comme précédemment , on utilise une feuille de cahier.

Vous constatez qu’on ne peut pas donner la mesure exacte de la longueur du [ C D ]. Mais on peut dire que «  CD > 7 » et « CD < 8 » On dit alors que : «  CD est comprise entre 7 et 8  » « 7 » est la valeur approchée à « 1 » prés par défaut de CD ( unité u ) « 8 » est la valeur approchée à « 1 » prés par excès de CD ( unité u )

Remarque : On écrit aussi

7 u < C D < 8 u

( c’est un encadrement de longueur )

Exercice

On vous donne une unité de longueur  « u » :

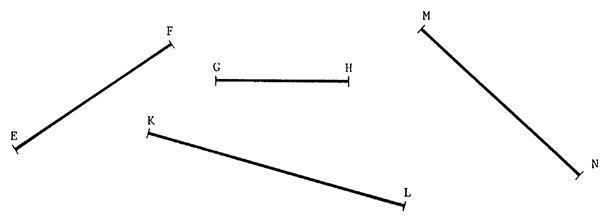
Et 4 segments ( ci-dessous)  : On vous demande de donner un encadrement des mesures de leurs longueurs avec les unités « u » , « cm » , « mm ». Reporter les résultats dans le tableau ci-dessous.

Info +instrument ++

Unité « u »

Centimètre

Millimètre

EF

..…….< E F < …….

..…….< E F < …….

GH

KL

MN

Remarque : Vous constatez que certains segments qui n’ont pourtant pas la même longueur ont des mesures de longueur qui ont le même encadrement pour une unité donnée. Cependant, cet encadrement peut changer si l’on change d’unité. Plus l’unité est petite, plus l’encadrement est serré , donc , plus précis.

Info ++

4°) Graduation régulière – mesurage avec des nombres à virgule.

On donne une demi-droite [ O x , et une unité de longueur « u »

A partir de « O » on a reporté la longueur « u » de proche en proche….( en partant de la gauche et en se déplaçant vers la droite , notre sens de lecture d’un texte ) On a ainsi obtenu des points auxquels on a fait correspondre successivement les nombres « 1 » ; « 2 » ; « 3 » ; »4 » ; « 5 » ; « 6 » ; …en « O » on fait correspondre le « 0 » (zéro) On a fabriqué une graduation régulière.

Activité : On voudrait mesurer la longueur [ O M ] avec l’unité « u »

On constate que «  3 < OM < 4 » la mesure de la longueur de [ O M ] n’est pas un nombre entier.

Nous décidons de partager en 10 segments superposables chacun des segments de longueur « u » déterminés par la graduation. On obtient ainsi une sous graduation :

On remarque que le point « M » est placé au 7^ème trait de la « subdivision » après le point repéré par « 3 ». On écrira alors «  OM = 3,7 » avec l’unité « u ».

On demande de déterminer de même les mesures ci- dessous faites avec l’unité « u ».

OA = ……………2,5………… ;

OC = ……………4,3…………

DC = ………4,6…….

DM = ………3………….

OB = ……………1,8……………

O D = ……………0,7…………

MA = ………1,2 …………

MC = ………0,6……………

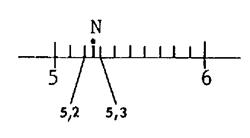
Nous considérons le point « N ». Il n’est pas placé sur un trait de la subdivision. Vous pouvez donner un encadrement de « ON » ( avec l’unité « u »)  5,2 < ON < 5 , 3

Pour avoir une mesure plus précise , on va partager chaque petit segment en 10 segments (superposables , de même écartement.

On vous donne ci-dessous un agrandissement d’une parie de la figure précédente : ( entre « 5 » et « 6 » )

On constate que « N3 est placé au « 6^ème »trait après le point repéré par « 5,2 » ; on écrira alors «  ON = 5, 26 »

On vous demande de donner la valeur (de la position du point ) « OF = ……5,02….. » ; et «  OE = ……5,78……….. »

On peut recommencer à partager les petits segments en 10 segments superposables , on trouvera alors des longueurs ayant pour mesure avec l’unité « u » des nombres tels que :

4,846

59,293

0,118

0,073

0,004

Etc……

En continuant encore , on trouverait des longueurs ayant pour mesure avec l’unité « u » des nombres tels que :

4,7843

57,53079

0,000654

Etc……

Remarque 1 : Dans la réalité , de telles découpages (constructions) ne sont pas possibles car après plusieurs subdivisions , on ne « verrait » plus rien . mais rien ne nous empêche de les imaginer. D’autre part , ces figures ne sont jamais exactes mais nous considérons qu’elles représentent des figures parfaites.

Remarque 2 : Il est très difficile de donner une mesure avec précision car : Les objets à mesurer ne sont pas parfaits. Les instruments de mesure ne sont pas assez précis. L’œil ne peut pas apprécier des écarts très petits. En fait, une mesure est toujours une valeur approchée.

TRAVAUX AUTO FORMATIFS

CONTROLE :

Voir : chapitre par chapitre pour poser des questions….

EVALUATION

Refaire des exercices du cours

Aller revoir les activités dus cours..

INTERDISCIPLINARITE